-
Email : info(at)proffi-m.de
Ferrero-Küsschen
Fehlermeldung
Deprecated function: The each() function is deprecated. This message will be suppressed on further calls in FieldCollectionItemEntity->fetchHostDetails() (Zeile 313 von /www/htdocs/w0127817/beta.proffi-m.de/sites/all/modules/field_collection/field_collection.entity.inc).| Klasse | Schulstufe | Thema | Themengebiet | Schwierigkeit |
|---|---|---|---|---|
| 10 | Sekundarstufe I | Oberfläche und Volumen von Pyramiden bestimmen | Größen und Messen, Raum und Form, Zahlen und Operationen | ** |
| Heuristsche Hilfsmittel | Heuristische Prinzipien | Heuristische Strategien |
|---|---|---|
| Informative Figur, Tabelle, Gleichungen | Zerlegungs- und Ergänzungsprinzip, Invarianzprinzip, Symmetrieprinzip | Vorwärtsarbeiten, Rückwärtsarbeiten, Analogieschlüsse, Rückführung von Unbekanntem auf Bekanntes |
Aufgabenstellung
Zu Weihnachten soll eine Sonderverpackung für Ferrero Küsschen angefertigt werden. Diese soll die Form einer Pyramide besitzen und zwischen 30 und 40 Ferrero Küsschen beinhalten.
- Wie viel Pappkarton wird benötigt um die Verpackung herzustellen (Klebelaschen können vernachlässigt werden)?
- Vergleiche deinen Lösungsweg und Ergebnis mit denen deiner Mitschüler. Welche Lösung gefällt euch am besten. Begründe!
Quellenangabe:
http://www.problemloesenlernen.dvlp.de/files/42/geometrie_pyramide_neu.pdf
Lösungsvariante 1
1. Schritt: Maße eines Ferrero Küsschens ermitteln durch Messen
|
Höhe \(h_k=20mm\) Breite \(b_k=28mm\) Tiefe \(t_k=25mm\) |
 |
2. Schritt: Pyramide stapel
|
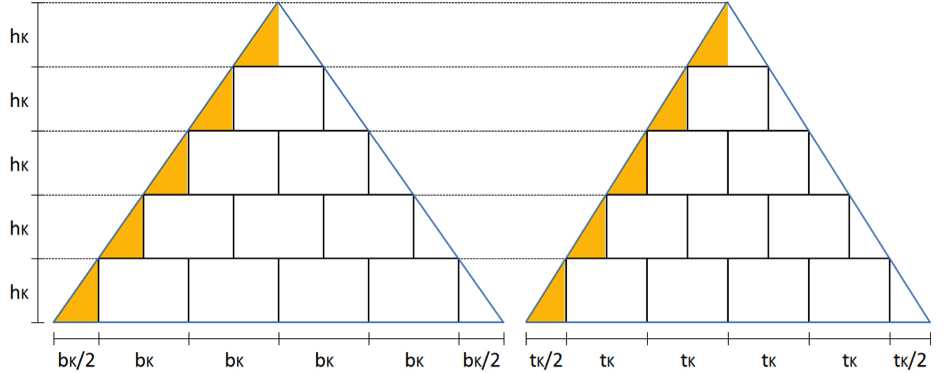
Es gibt mehrere Varianten diese Aufgabe zu lösen. Wir haben uns für die folgende Lösung entschieden: Die Küsschen werden in jeder Ebene der Pyramide in n Reihen und n Spalten angeordnet, sodass sich die Anzahl der Küsschen pro Ebene durch n² berechnen lässt. Obwohl die Küsschen eine rechteckige Grundfläche haben, werden die Küsschen auf quadratischen Ebenen angeordnet, sodass immer kleine Lücken zwischen den Reihen entstehen. Das heißt jedes Küsschen steht auf einem quadratischen Platz von 28mm x 28mm. Jede tiefere Ebene hat eine um ein Küsschen breitere Grundseite als ihr Vorgänger. Die Tabelle zeigt, wie viele Ebenen die Sonderverpackung haben müsste, um auf eine Anzahl von 30 – 40 Küsschen zu kommen.
|
 |
||||||||||||||||||||||||
|
 |
| Die Pyramide besteht also aus vier Ebenen mit insgesamt 30 Ferrero Küsschen. |
3. Schritt: Verpackungsmaße bestimmen
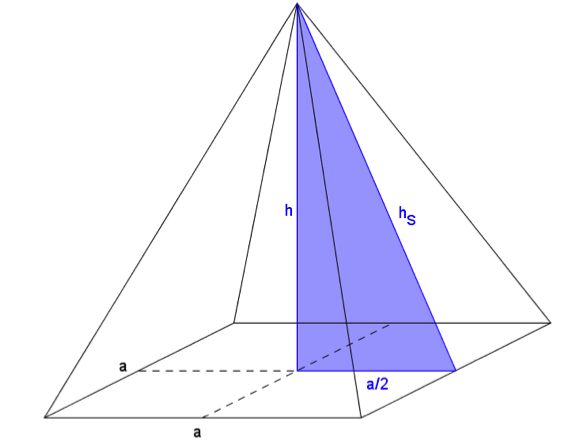
Um die Oberfläche der Sonderverpackung zu berechnen, werden die quadratische Grundfläche und die vier dreieckigen Seitenflächen der Pyramide benötigt. Da die Grundfläche der Pyramide quadratisch gewählt wurde, braucht aus Symmetriegründen nur eine Seitenansicht betrachtet werden, um alle relevanten Maße der Pyramide zu bestimmen.
|
Die Seitenflächen der Pyramide liegt auf den Ecken der Küsschen auf. Dadurch ergeben sich Teile der Pyramide, die nicht gefüllt werden können (in der Skizze gelb markiert). Das bedeutet, dass die Höhe der Pyramide etwas größer als die gestapelten Küsschen sein muss und die Grundseite etwas breiter als die Breite der untersten Ebene. Aufgrund der Art und Weise, wie die Küsschen gestapelt sind, entspricht die Breite der gelben Fläche der Hälfte der Breite eines Küsschens und die Höhe der gelben Fläche entspricht der Höhe eines Küsschens. Daraus ergibt sich für die Höhe h der Pyramide \(h=5\cdot h_k=5\cdot 20mm=100mm=10cm\) und die für die Grundseite a der quadratischen Grundfläche \(a=5\cdot b_k=5\cdot28mm=140mm=14cm.\) |
 |
|
Um die Fläche der dreieckigen Seiten der Pyramide zu berechnen wird die Höhe dieser Seitenflächen benötigt. Die Höhe h der Pyramide, die Mittellinie auf der Grundfläche und die Höhe der Seitenflächen bilden ein rechtwinkliges Dreieck. Die Höhe \(h_s\) der Seitenflächen lässt sich mit dem Satz des Pythagoras berechnen: \({h_s}^2=h^2+(\frac{a}{2})^2=(10cm)^2+(7cm)^2=149cm^2\\ h_s=\sqrt{149}cm.\) Für die Oberfläche der Sonderverpackung ergibt sich somit: \(O_{Pyramide}=O_{Grundfläche}+O_{Mantelfläche}\\ O_{Pyramide}=a^2+4\cdot\frac{1}{2}\cdot a\cdot h_d\\ O_{Pyramide}=(14cm)^2+2\cdot 14cm\cdot\sqrt{149}cm\\ O_{Pyramide}\approx 537,78cm^2.\) |
 |
Antwort
Die Sonderverpackung von Ferrero Küsschen könnte eine Höhe von 10cm und eine quadratische Grundfläche mit einer Seitenlänge von 14cm haben. In diese Verpackung würden 30 Küsschen passen und es wird etwa 538cm² Pappkarton benötigt.
Im Aufgabenteil 2. sollen die Schülerinnen und Schüler die verschiedenen Lösungsvarianten miteinander vergleichen. Wir möchten an dieser Stelle lediglich einige Merkmale angeben, an denen die Lösungen verglichen werden könnten, um eine gute (oder sogar die beste) Lösung zu finden.
Die offensichtlichste Betrachtungsweise ist der Vergleich der Oberflächen oder der Vergleich der Anzahl der Küsschen, die die verschiedenen Verpackungen fassen können. Interessant wäre auch ein Vergleich der Kennzahl Oberfläche pro Küsschen. Da es sich um eine Produktverpackung handelt, sind hier auch Argumentationen über das Aussehen denkbar, die allerdings wenig mathematisch sein dürften.
Lösungsvariante 2
|
Anstatt die Küsschen versetzt zu stapeln, können sie auch direkt übereinander gestapelt werden. Das bedeutet, dass sich auf jeder Ebene als Grundseite jeweils nur eine ungerade Anzahl an Küsschen ergibt. Die Küsschen werden wieder so angeordnet, dass sich quadratische Ebenen ergeben. Die Tabelle zeigt, wie die Küsschen gestapelt werden, um in der Summe auf eine Anzahl von 30 – 40 Küsschen zu kommen:
|
 |
||||||||||||||||||||
|
Die Pyramide besteht also aus drei Ebenen mit insgesamt 35 Ferrero Küsschen (siehe Bild). Da die Grundfläche der Pyramide quadratisch gewählt wurde, braucht aus Symmetriegründen nur eine Seitenansicht betrachtet werden, um alle relevanten Maße der Pyramide zu bestimmen. |
|||||||||||||||||||||
|
Die Seitenflächen der Pyramide liegen auf den Ecken der Küsschen auf. Dadurch ergeben sich Teile der Pyramide, die nicht gefüllt werden können (in der Skizze gelb und markiert). Das bedeutet, dass die Höhe der Pyramide etwas größer als die gestapelten Küsschen sein muss und die Grundseite etwas breiter als die Breite der untersten Ebene. Das grüne Dreieck ist zu den gelben Dreiecken ähnlich. Da die Grundseite des grünen Dreiecks halb so lang wie die des gelben Dreiecks ist, ist auch die Höhe halb so groß wie die des gelben Dreiecks (gleiche Seitenverhältnisse in ähnlichen Dreiecken). Daraus ergibt sich für die Höhe h der Pyramide \(h=5\cdot h_k=3,5\cdot 20mm=70mm=7cm\) und die für die Grundseite a der quadratischen Grundfläche \(a=7\cdot b_k=7\cdot 28mm=196mm=19,6cm\) |
 |
||||||||||||||||||||
|
Analog zur ersten Lösung berechnet sich die Höhe \(h_s\) der Seitenflächen: \({h_s}^2=h^2+(\frac{a}{2})^2=(7cm)^2+(9,8cm)^2=145,04cm^2\\ h_s=\sqrt {145,04}cm.\) Für die Oberfläche der Sonderverpackung ergibt sich somit: \(O_{Pyramide}=O_{Grundfläche}+O_{Mantelfläche}\\ O_{Pyramide}=a^2+4\cdot\frac{1}{2}\cdot a\cdot h_s\\ O_{Pyramide}=(19,6cm)^2+2\cdot 19,6cm\cdot\sqrt{145,04}cm\\ O_{Pyramide}\approx 856,26cm^2\) |
 |
||||||||||||||||||||
Antwort
Die Sonderverpackung von Ferrero Küsschen könnte eine Höhe von 7cm und eine quadratische Grundfläche mit einer Seitenlänge von 19,6cm haben. In diese Verpackung würden sogar 35 Küsschen passen, allerding wird für die Verpackung etwas mehr Pappkarton benötigt, nämlich etwa 856cm².
Lösungsvariante 3
| Beide Lösungsvorschläge lassen sich noch variieren, indem die Küsschen nicht auf einer quadratischen Grundfläche angeordnet, sondern so dicht wie möglich zusammengestellt werden. Daraus ergibt sich eine rechteckige Grundfläche. |
 |
|
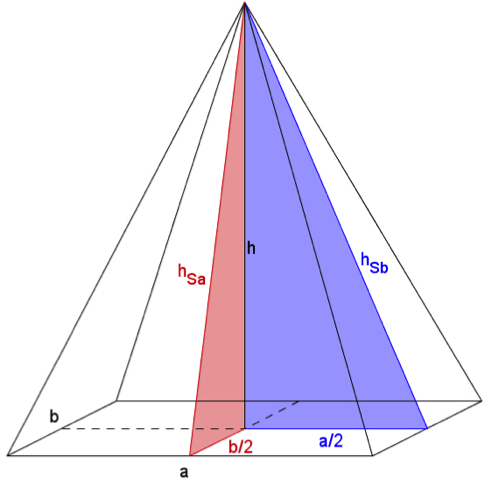
Hier führen wir die Variation der Lösung aus Aufgabenteil 1. vor, die Variation der alternativen Lösung aus Aufgabenteil 2. erfolgt analog. Mit der gleichen Argumentation wie oben ergeben sich für die rechteckige Grundfläche der Pyramide die Seitenlängen \(a=5\cdot b_k=5\cdot 28mm=140mm=14cm\\ b=5\cdot t_k=5\cdot 25mm=125mm=12,5cm.\) Die Höhe h der Pyramide bleibt unverändert, also ist die Höhe h=10cm. |
 |
|
Die Mantelfläche der Pyramide setzt sich aus vier Dreiecken zusammen, wobei die gegenüberliegenden Seitenflächen jeweils kongruent sind. Analog zur ersten Lösung lassen zwei rechtwinklige Dreiecke identifizieren. Zusammen mit der Höhe h der Pyramide und den Mittellinien auf der Grundfläche bilden die Höhen \(h_{sa}\) und \(h_{sb}\) der Seitenflächen rechtwinklige Dreiecke und lassen sich mit dem Satz des Pythagoras berechnen. Für die Seitenfläche an den langen Kanten a der Grundfläche ergibt sich eine Höhe \(h_{sa}\): \({h_{sa}}^2=h^2+(\frac{b}{2})^2=(10cm)^2+(6,25cm)^2\\ {h_{sa}}^2\approx 139,1cm^2\\ h_{sa}\approx\sqrt{139,1}cm.\) Für die Seitenfläche an der kurzen Kante b der Grundfläche ergibt sich eine Höhe \(h_{sb}\): \({h_{sb}}^2=h^2+(\frac{a}{2})^2=(10cm)^2+(7cm)^2=149cm^2\\ h_{sb}=\sqrt{149}cm.\) Für die Oberfläche der Sonderverpackung ergibt sich somit: \(O_{Pyramide}=O_{Grundfläche}+O_{Mantelfläche}\\ O_{Pyramide}=a\cdot b+2\cdot\frac{1}{2}\cdot a\cdot h_{sa}+2\cdot \frac{1}{2}\cdot b\cdot h_{sb}\\ O_{Pyramide}\approx 14cm\cdot 12,5cm+14cm\cdot\sqrt{139,1}cm+12,5cm\cdot\sqrt{149}cm\\ O_{Pyramide}\approx 492,7cm^2.\) |
 |
Antwort
Die Sonderverpackung von Ferrero Küsschen könnte ebenso eine Höhe von 10cm und eine rechteckige Grundfläche mit den Seitenlängen 14cm und 12,5cm haben. In diese Verpackung würden ebenfalls nur 30 Küsschen passen, allerdings wird für diese Verpackung auch nur etwa 493 cm² Pappkarton benötigt.
Inhaltsbezogene Kompetenzen
„Die Schülerinnen und Schüler planen Messungen in ihrer Umwelt, führen diese gezielt durch, entnehmen Maßangaben aus Quellenmaterial, führen Berechnungen durch und bewerten die Ergebnisse sowie den gewählten Weg“
(Niedersächsisches Kultusministerium 2006, S. 30)
Um das Problem mathematisch lösen zu können, benötigen die Schülerinnen und Schüler die Maße ihrer Pyramide. Folglich planen sie, welche Messungen in ihrer Umwelt durchgeführt werden müssen und führen diese dann auch gezielt durch. Alternativ dazu ein Ferrero Küsschen zu messen, könnten die Daten auch aus Quellenmaterial wie einem Buch oder dem Internet entnommen werden. Anschließend führen sie Berechnungen durch und bewerten die Ergebnisse sowie den gewählten Weg, was explizit in Aufgabenteil b gefordert ist.
„Die Schülerinnen und Schüler zeichnen Schrägbilder von Zylinder, Pyramide und Kegel, entwerfen Körpernetze und stellen Modelle her“
(Niedersächsisches Kultusministerium 2006, S. 32)
Eine zentrale Kernkompetenz ist das Benutzen von Schrägbildern. Konkret bei dieser Aufgabe wird mit dem Schrägbild einer Pyramide gearbeitet, sodass es sinnvoll ist, beim Lösen dieser Aufgabe auch ein Schrägbild einer Pyramide zu zeichnen und räumlich vorzustellen, welche Strecken zur Berechnung der Oberfläche gegeben und welche noch mathematisch ermittelt werden müssen.
„Die Schülerinnen und Schüler wenden den Satz des Thales und den Satz des Pythagoras bei Konstruktionen, Berechnungen und Beweisen an“
(Niedersächsisches Kultusministerium 2006, S. 32)
Zur Berechnung der Seitenflächen wird die Seitenhöhe benötigt. Um diese zu ermitteln benötigen die Schülerinnen und Schüler den Satz von Pythagoras. Die Schülerinnen und Schüler müssen dazu nicht nur den Satz von Pythagoras kennen, sondern auch in der Planfigur wiederfinden (Wo ist das Dreieck? Wo ist der rechte Winkel? Welche Maße stehen mir bei der Berechnung zur Verfügung?).
Kompetenzen aus den Bereichen Funktionaler Zusammenhang und Daten und Zufall werden für diese Aufgabe nicht angesprochen.
Zusammenfassung: Es werden fast alle Kompetenzbereiche durch diese Aufgabe erfasst. Den Schwerpunkt sehen wir dabei in den Bereichen:
- Probleme mathematisch lösen, weil die Schülerinnen und Schüler kein starres Schema für diese Aufgabe haben, sondern kreativ daran herangehen sollen, um mit Hilfe von Mathematik eine Lösung für diesen realen Kontext finden sollen.
- Raum und Form, weil das Schrägbild einer Pyramide ein wesentlicher Aspekt dieser Aufgabe ist.
- Mathematisch Kommunizieren, weil der Aufgabenteil b ausdrücklich dazu auffordert seinen eignen Lösungsweg mitzuteilen, andere Lösungswege nachzuvollziehen und diese miteinander zu vergleichen.
Um die Aufgabe zu lösen, benötigen die Schülerinnen und Schüler verschiedene Fähigkeiten und Fertigkeiten. Zunächst sollten die Schülerinnen und Schüler eine klare Vorstellung von einer Pyramide haben, die zur mathematischen Definition passt. Sie müssen wissen, was mit dem Begriff Oberfläche gemeint ist und wie man eine Oberfläche berechnet. Das Prinzip des Zerlegens in bekannte Teilflächen soll bekannt sein. Die Formeln für die Flächenberechnung (insbesondere Rechteck, Quadrat und Dreieck) sollten ebenfalls bekannt sein. Die Darstellung von dreidimensionalen Figuren mittels Schrägbilder sollte bekannt sein. Ein gutes räumliches Vorstellungsvermögen ist hierbei hilfreich. Die Schülerinnen und Schüler müssen mehrfach den Satz des Pythagoras anwenden. Dieser Satz muss also ebenfalls bekannt sein und der Umgang mit den entsprechenden Werkzeugen zur Umformung der quadratischen Terme und Gleichungen (insbesondere Wurzel- und Potenzgesetze) sollte geläufig sein.
Des Weiteren sollten die Schülerinnen und Schüler in der Lage sein, sich Informationen eigenständig zu besorgen, ohne dass sie diese durch einen Text vorgegeben bekommen. Außerdem müssen sie eine Realsituation fachgerecht modellieren. Ihnen sollten also die grundlegenden Werkzeuge und Kenntnisse zum Erstellen und zum Umgang mit mathematischen Modellen zur Verfügung stehen.
Mit Blick auf die verwendeten Formeln und Sätze, lässt sich diese Aufgabe bereits in der Jahrgangsstufe 8 umsetzen, da aber in Jahrgangstufe 8 die Pyramide noch nicht behandelt wird und keine Schrägbilder von Pyramiden angefertigt werden, ist dies eher für die Klasse 9 zu empfehlen. Die Schülerinnen und Schülersollten gegen Ende der Jahrgangstufe 9 alle vorausgesetzten Kompetenzen zur Lösung der Aufgabe erworben haben.
Die von uns gewählte Aufgabe spricht gleich mehrere Kompetenzbereiche des niedersächsischen Kerncurriculums für das Gymnasium in Schuljahrgänge 5 -10 an. In erster Linie ist diese Aufgabe dem Kompetenzbereich Probleme mathematisch lösen zu zuordnen, da aus diesem Bereich gleich mehrere Kernkompetenzen erfasst werden, wie beispielsweise inner- und außermathematische Problemstellungen zu erfassen und fehlende Informationen zu beschaffen (ausführliche Begründung siehe weiter unten). Um die Aufgabe lösen zu können, sollen die Schülerinnen und Schüler die Realsituation in das vorgegebene mathematisches Modell überführen, sodass auch der Kompetenzbereich des mathematischen Modellierens mit dieser Aufgabe angesprochen wird. Da die Schülerinnen und Schüler in Aufgabenteil b ausdrücklich dazu aufgefordert sind ihre Lösungswege untereinander zu vergleichen, kann diese Aufgabe auch dem Kompetenzbereich Kommunizieren zugeordnet werden. Der Kompetenzbereich Mathematisch Argumentieren wir bei dieser Aufgabe ebenfalls angesprochen, weil die Schülerinnen und Schüler mehrere Lösungswege vergleichen und bewerten sollen.
Durch das Zeichnen von Schrägbildern und das Benutzen von Variablen werden auch die Kompetenzbereiche Mathematische Darstellungen verwenden und Mit symbolischen, formalen und technischen Elementen der Mathematik umgehen abgedeckt. Allerdings liegt der Schwerpunkt dieser Aufgabe nicht auf diesen zuletzt genannten Kompetenzbereichen.
Der Kompetenzbereich Zahlen und Operatoren wird erfasst, weil die Schülerinnen und Schüler zum Lösen der Aufgabe die Oberfläche einer Pyramide berechnen müssen. Der Kompetenzbereich Größen und Messen wird ebenfalls abgedeckt, da die Schülerinnen und Schüler bestimmte Ergebnisse mit dem Lineal messen, mit dem Taschenrechner berechnen und zum weiterrechnen gegebenenfalls sinnvoll runden müssen. Hauptsächlich ist diese Aufgabe dem Kompetenzbereich Raum und Form zu zuordnen, da Schrägbilder, der Satz des Pythagoras und andere Kernkompetenzen aus diesem Bereich benutzt werden müssen.
Prozessbezogene Kompetenzen
„Die Schülerinnen und Schüler stellen sich inner- und außermathematische Probleme und beschaffen die zu einer Lösung noch fehlenden Informationen“
(Niedersächsisches Kultusministerium 2006, S. 15)
Die Schülerinnen und Schüler stellen sich bei dieser Aufgabe inner- und außermathematischen Problemen, da sie 30-40 Ferrero Küsschen in einer Pyramidenform anordnen müssen, wobei dieser Teil der Aufgabe mehrere Möglichkeiten zulässt. Um das Problem mathematisch lösen zu können, müssen sich die Schülerinnen und Schüler die noch fehlenden Informationen über die Maße der Küsschen (Länge, Breite, Höhe) beschaffen, indem sie beispielsweise ein Küsschen vermessen, im Internet nach den Größenangaben recherchieren oder sinnvoll schätzen.
„Die Schülerinnen und Schüler verstehen Überlegungen von anderen zu mathematischen Inhalten, überprüfen diese auf Schlüssigkeit und gehen darauf ein“
(Niedersächsisches Kultusministerium 2006, S. 24)
Durch die offene Aufgabenstellung wird es vermutlich verschiedene Lösungswege bei den Schülerinnen und Schülern geben. Diese sollen in Aufgabenteil b verglichen und bewertet werden. Dazu müssen die Schülerinnen und Schüler nicht nur ihre eigenen Überlegungen anderen verständlich mitteilen können, sondern ebenso die Überlegungen von anderen nachvollziehen können, um darauf einzugehen.
„Die Schülerinnen und Schüler zeichnen Schrägbilder von Körpern, entwerfen Netze und stellen Modelle her“
(Niedersächsisches Kultusministerium 2006, S. 19)
Die Schülerinnen und Schüler konstruieren um die Stufenpyramide aus Ferrero Küsschen eine weitere Pyramide, welche als Modell für die Verpackung dienen soll. Sie nutzen das Schrägbild, um die fehlenden Maße der Pyramide für die Berechnung der Verpackung ermitteln zu können.
Heuristische Hilfsmittel:
Als heuristisches Hilfsmittel wurden informative Figuren und eine Tabelle verwendet.
- Die Gesamtanzahl der Küsschen wurde in einer Tabelle dokumentierten, um die Grenze von 30 – 40 Küsschen nicht zu überschreiten. Da zu weissen war wie viele Ebenen die Pyramide haben wird und wie viele Küsschen dazu auf der untersten Ebene angeordnet werden müssen, wurde ein Schrägbild einer Pyramide angefertig.
- Diese informative Figur diente neben der Visualisierung auch dazu, die zur Berechnung erforderlichen Seiten mit Variablen zu benennen, um später Formeln anwenden zu können. Eine weitere Skizze vom Querschnitt der Pyramide half bei der Bestimmung der Breite und der Höhe der Pyramide. Diese Skizze verdeutlichte am mathematischen Modell, wie die Verpackung jeweils auf den Außenkanten der Küsschen aufliegt.
Heuristische Strategien:
Als heuristische Strategie wurde eine Kombination aus Vorwärts- und Rückwärtsarbeiten benutzt. Zusätzlich wurden Analogieschlüsse sowie die Rückführung von Unbekanntem auf Bekanntes gemacht.
- Die Rückwärtsarbeiten wurde beim Nachdenken benutzt, wie die Küsschen gestapelt werden könnten, um die Form einer Pyramide nachzuahmen.
- Beim Bestimmen von Pyramidengrößen wurde die Strategie des Vorwärtsarbeitens benutzt. Mit Hilfe der Dreiecke aus dem Schrägbild ließ sich die Berechnung der Höhe der Seitenflächen als Analogieschluss auf den bereits bekannten Satz des Pythagoras zurückführen – Rückführung von Unbekanntem auf Bekanntes.
- Da die Höhe der Pyramide sich analog zu Breite der Pyramide ergeben hat, wurde auch Analogieschluss verwendet.
Heuristische Prinzipien:
Von den bekannten heuristischen Prinzipien, wurden das Zerlegungs- und Ergänzungsprinzip sowie das Invarianzprinzip benutzt.
- In der Aufgabenstellung wurde nach der Oberfläche einer Pyramide gefragt. Die Oberfläche dieses Körpers setzt sich aus Rechtecken und Dreiecken zusammen. Darüber hinaus wurden im letzten Schritt die berechneten Maße in die jeweiligen Formeln für die Flächenberechnung eingesetzt. Die Flächen der vier Seiten und der Grundfläche wurden dann addiert und es wurde eine Antwort formuliert. Also hier wurde das Zerlegungs- und Ergänzungsprinzip angewedet.
- Das Invarinazprinzip wurde angewendet, indem die Gesamtanzahl an Küsschen zwischen 30 und 40 liegen sollte, wobei die Form einer Pyramide veränderbar war.
Allgemeine Analyse
Den Schülerinnen und Schülern können (je nach subjektivem Empfinden) unterschiedliche Schwierigkeiten begegnen.
Bereits die Anordnung der Küsschen in Pyramidenform konnte eine erste Hürde darstellen, da die Aufgabe nicht eindeutig lösbar ist. Die Schülerinnen und Schüler müssen sich für eine Variante entscheiden, was bei geringen Selbstvertrauen in die eigenen mathematischen Kenntnisse und Fähigkeiten zu Unsicherheit führen könnte.
Einige Schülerinnen und Schüler werden sich eventuell für eine rechteckige Grundfläche entscheiden, da es für sie die einzige offensichtliche Lösung ist. Dies führt bei der weiteren Bearbeitung zu einer aufwendigeren Rechnung, als bei einer quadratischen Grundfläche. Das bedeutet, dass die Schülerinnen und Schüler durch ihre eigene Entscheidung zu Beginn der Aufgabe weitere Schwierigkeiten generieren. Um dies zu überblicken ist ein hohes Maß an Metakognition sowie eine gute Struktur und Planung des eigenen Lösungswegs notwendig.
Die Überführung der mit Küsschen aufgestellten Stufenpyramide in ein mathematisches Modell in Form einer Pyramide könnte weitere Schwierigkeiten hervorrufen. Insbesondere die Bestimmung der Höhe der Pyramide und die Kantenlängen der Grundfläche sind nicht offensichtlich, da die Höhe und Kantenlänge der Verpackung nicht der Höhe und Kantenlänge der aufgestellten Stufenpyramide entsprechen. An dieser Stelle ist ein gutes räumliches Vorstellungsvermögen hilfreich. Durch Erstellen einer informativen Figur kann dieses Problem deutlich entschärft werden.
Die anschließend durchzuführenden Rechnungen (Seitenflächenhöhe mit dem Satz des Pythagoras, Flächeninhalte der dreieckigen Seitenflächen, etc.) können je nach Kenntnis- und Übungsstand der Schülerinnen und Schüler ebenfalls als schwierig empfunden werden.
Sollen sich die Schülerinnen und Schüler die Berechnung der Oberfläche einer Pyramide selbst aus den Flächenberechnungen von Dreieck und Rechteck herleiten, müssen sie die Oberfläche der Pyramide in diese Teilflächen zerlegen, was ebenfalls einen hohen Anspruch an das räumliche Vorstellungsvermögen stellt.
Da dieser Aufgabe 5 Punkte vergeben wurden, wurde diese Aufgabe mit ** gekennzeichnet. Hier die Analyse:
Sprachlogische Komplexität:
Die Aufgabenstellung besteht aus einem kurzen Text ohne verwinkelte Nebensätze. Zuerst werden knapp die Informationen gegeben und anschließend der Arbeitsauftrag erteilt. Dies entspricht auch den Schritten der mathematischen Bearbeitung. Zudem werden nur relevante Informationen gegeben. Aufgrund dieser Beobachtungen könnte man die Stufe 0 hinsichtlich der sprachlogischen Komplexität zuordnen.
Kognitive Komplexität:
Bei der ausgewählten Aufgabe handelt es sich um eine Problemlöseaufgabe, bei der die Schülerinnen und Schüler individuelle Barrieren überwinden müssen, um den Ausgangszustand in den Zielzustand zu überführen.
Vor der Bearbeitung der eigentlichen Aufgabe (Bestimmung der Maße und des Oberflächeninhaltes einer Pyramide) müssen die Schülerinnen und Schüler zunächst überlegen, wie sich die Küsschen als Pyramide anordnen lassen, da dieses nicht vorgegeben ist. Dabei müssen diese die Nebenbedingung beachten, dass in der neuen Verpackung 30-40 Ferrero Küsschen enthalten sein sollen. Anschließend müssen die Schülerinnen und Schüler unter Zuhilfenahme verschiedener Heurismen die Aufgabe lösen und das Modell aus verschiedenen Blickwinkeln erfassen, welche sich mittels verschiedener Ansichten der Pyramide (Frontalansicht, Vogelperspektive, Schrägbild) erfassen lassen. Durch eine Skizze kann die kognitive Komplexität etwas reduziert werden. Zusätzlich bauen alle Teilergebnisse aufeinander auf, wodurch ein Fehler starke Auswirkungen auf das Endergebnis hat. Aufgrund dieser Beobachtungen könnte man die Stufe 2 hinsichtlich der kognitiven Komplexität zuordnen.
Formalisierung von Wissen:
Zur Berechnung der Aufgabe müssen die Schülerinnen und Schüler die verschiedenen Strecken in der Pyramide benennen und anschließend die verwendeten Formeln korrekt mit ihren Bezeichnungen verwenden. Dazu sind unter anderem Rückgriffe auf eigene Repräsentationen notwendig, je nachdem ob eine oder mehrere Skizzen erstellt wurden. Ob die dabei entstanden Ergebnisse logisch sind, können die Schülerinnen und Schüler anhand der bereits bekannten Werte ermitteln und reflektieren. Dies geht über das Finden einfacher formaler Darstellungen hinaus. Aufgrund dieser Beobachtungen könnte man die Stufe 2 hinsichtlich der Formalisierung von Wissen zuordnen.
Formelhandhabung:
Zur Bearbeitung der Aufgabe werden Formeln verwendet, deren Umstellung nach einer anderen Variablen nicht nötig ist. Algebraische Umformungen werden nur in einem geringen Maße bei der Anwendung des Satzes von Pythagoras verwendet. Dies entspricht der Verwendung einer bekannter Lösungsroutine. Aufgrund dieser Beobachtungen könnte man die Stufe 1 hinsichtlich der Formelhandhabung zuordnen.
Stufenzuordnung:
Formalisierung von Wissen
Stufe 2
Formelhandhabung
Stufe 1
Kognitive Komplexität
Stufe 2
Sprachlogische Komplexität
Stufe 0
Hilfestellungen:
Für Schülerinnen und Schüler, die Schwierigkeiten damit haben die Kantenlänge der Grundfläche und die Höhe der Pyramide zu bestimmen (nicht die der Stufenpyramide aus Küsschen, sondern die Maße der Verpackung!), bieten sich folgende Hilfestellungen an:
| Allgemein-Strategische Hilfestellungen | Inhaltsorientierte Strategische Hilfestellungen | Inhaltliche Hilfestellungen |
| Siehe dir die Skizze genau an. Fällt dir etwas auf? | Gibt es besondere Dreiecke die dir weiterhelfen können | Suche rechtwinklige Dreiecke! |
| Kennst du eine ähnliche Aufgabe? Wenn ja, wie bist du bei dieser vorgegangen? | Kannst du die Figur in Teilfiguren zerlegen und anders zusammensetzen? | Welcher Zusammenhang besteht zwischen den Dreiecken (Lücken) und den Vierecken (Küsschen)? |
| Was weißt du bereits und was fehlt dir, um das Problem weiter zu lösen? | Gibt es Hilfslinien, die dir weiterhelfen können? | Zu welchen Dreiecken ist das Dreieck, welches die Spitze der Pyramide darstellt, ähnlich? |
Für Schülerinnen und Schüler, die Schwierigkeiten damit haben die Seitenhöhe der Pyramide mittels Pythagoras zu bestimmen, bieten sich folgende Hilfestellungen an:
| Allgemein-Strategische Hilfestellungen | Inhaltsorientierte Strategische Hilfestellungen | Inhaltliche Hilfestellungen |
| Zeichne eine Skizze oder ein Schrägbild. | Kannst du in deine Skizze hilfreiche Hilfslinien einzeichnen? | Suche rechtwinklige Dreiecke! |
| Was weißt du bereits und was fehlt dir um das Problem weiter zu lösen? | Gibt es besondere Dreiecke, die dir weiterhelfen können? | Mit welchem Satz kann man die dritte Seite eines rechtwinkligen Dreiecks bestimmen? |
| Kennst du eine ähnliche Aufgabe aus dem vergangenen Schuljahr? | Kannst du einen besonderen Satz aus der Geometrie anwenden? |
Erkennst du in deiner Skizze ein rechtwinkliges Dreieck, mit dessen Hilfe du die Seitenhöhe bestimmen kannst? |
Sozialformen:
Die Ich-Du-Wir-Methode kann bei dieser Aufgabe gut eingesetzt werden. Vor allem beim Aufgabenteil 2. bietet es sich an, nach einer Einzel- oder Partnerarbeitsphase die Lösungen aller Schüler zusammenzutragen, um so möglichst viele Möglichkeiten zu finden bzw. besprechen. Aber auch generell ist dieses Vorgehen geeignet, da jeder zuerst über eigene Strategien oder Ideen nachdenken kann, bevor er sich mit seinem Partner bespricht. Eine abschließende Behandlung der Aufgabe im Plenum kann Lösungsideen oder alternative Lösungsstrategien aufzeigen.
Differenzierungsmöglichkeiten:
Hinweise für die Leistungsschwächeren Schülerinnen und Schüler
Für leistungsschwache Schülerinnen und Schüler könnte die Aufgabe so abgewandelt werden, dass die neue Verpackung von Ferrero Küssen die Form eine Quaders haben sollte, der 30-40 Küssen enthalten soll. Dadurch würden viele Aspekte der Aufgabe, wie das Anwenden von Heurismen, erhalten bleiben. Auch bei dieser Variante müssten die Schülerinnen und Schüler überlegen, welche Formeln die benötigen und wie sie an die erforderlichen Maße gelangen können.
Eine andere Möglichkeit bestünde darin, mehrere Teilaufgaben zu formulieren. Dadurch würde man eine geleitet Lösung anbahnen und die schwächeren Schülerinnen und Schüler auf ihrem Lösungsweg unterstützen.
Eine kleinere Erleichterung (anstatt den gesamten Lösungsweg zu leiten) wäre die Bereitstellung einer Planfigur über die Anordnung der Küsschen. Ein zusätzliches Schrägbild würde vielen Schülerinnen und Schülern eine Orientierung beim Lösungsprozess bieten.
Hinweise für die Leistungsstärkeren Schülerinnen und Schüler
Für leistungsstarke Schülerinnen und Schüler könnte die Aufgabe erweitert werden, indem sie anschließend eine Pyramide mit dreieckiger Grundfläche modellieren sollen und darin 30-40 Küssen unterbringen sollen.
Eine andere Möglichkeit wäre einen Vergleich mit der traditionellen sechseckigen Form vorzunehmen. Dazu sollen die Schülerinnen und Schüler den Oberflächeninhalt einer sechseckigen Verpackung mit derselben Anzahl an Küsschen berechnen und beide Verpackungen anschließend hinsichtlich der Kosten für die Verpackungsmaterialien miteinander vergleichen.
Als dritte Variante könnte man die stärkeren Schülerinnen und Schüler dazu auffordern ein Bildungsgesetz zu ermitteln, mit dem sich die Anzahl der Ferrero Küsschen in einer beliebigen Ebene oder der gesamten Pyramide berechnen lässt.
Wir sind der Meinung, dass diese Aufgabe zu vielen Zwecken im Unterricht verwendet werden kann, da sie bei den Schülerinnen und Schüler viele Kompetenzen fördert. Beispielsweise könnte die Aufgabe als Einführung in das Thema Körperberechnung einer Pyramide verwendet werden. Das notwendige Wissen zur Berechnung von Rechtecken und Dreiecken ist bereits aus den unteren Jahrgangstufen bekannt, sodass die Schülerinnen und Schüler lediglich ihr Wissen über den Satz des Pythagoras und die Formeln für die Flächenberechnung (Dreieck/Rechteck) reaktivieren müssen. Eine Vorstellung über das Aussehen einer Pyramide sollte aus dem Alltag bekannt sein oder kann in Formelsammlungen oder dem Internet nachgeschaut werden.
Weiterhin kann diese Aufgabe im Zuge des Forschenden Lernens zur Anwendung kommen. Bei der Aufgabe handelt es sich um ein Problem, für dessen Lösung die Schülerinnen und Schüler individuelle Barrieren überwinden müssen. Beim Forschungsprozess entdecken die Schülerinnen und Schüler selbst Zusammenhänge. Dies ist mit einem Gefühl des Triumphs verbunden und motiviert für den weiteren Unterricht.
Als dritte Möglichkeit kann diese Aufgabe auch zum Produktiven Üben genutzt werden. Nachdem im Unterricht die Oberflächenformel für Pyramiden besprochen wurden, ist dies eine mögliche Anwendungsaufgabe, um die Verwendung der Formel zu üben und das mathematisch Modell der Pyramide in Alltagssituationen zu übertragen. Das erlernte Wissen wird im Problemlösekontext wiederholt und vertieft, um einen Alltagsbezug zu dem Thema herzustellen.
Bearbeitet von: Ana Kuzle, Stefan Bajorat, Tobias Bausch & Jana Wessels
Feedback
Wir freuen uns auf Ihre Anregungen und konstruktive Rückmeldung zum Material.
Copyright © 2014-2017 - Ana Kuzle