Baumstamm

Klasse Schulstufe Thema Themengebiet Schwierigkeit
9 Sekundarstufe I Größen mit Hilfe des Satz des Pythagoras bestimmen Funktionaler Zusammenhang, Größen und Messen, Raum und Form ***

Aufgabenstellung

Aus einem zylinderförmigen Baumstamm mit einem Durchmesser von ca. 80 cm werden drei 20 cm dicke Balken (siehe Grafik) herausgesägt.

Wie groß sind die maximalen Breiten und wie viel Prozent Abfall entsteht?

Quellenangabe:

madaba.de


Lösungsvariante 1:

Grundsätzlich wird zur Vereinfachung von perfekten Bedingungen mit symmetrischen Verhältnissen ausgegangen. Zuerst werden die maximalen Breiten (b1 und b2) berech net. Zunächst die des inneren Balkens (b2). Dafür werden die vorhandenen Informationen in der Skizze eingetragen, so dass die Nutzung des Satzes von Pythagoras leicht durchgeführt werden kann. Der Radius entspricht dabei der Hälfte des Durchmessers (d = 80 cm, damit r = 40 cm). Die Dicke der Balken (a) ist mit 20 cm gegeben, weshalb die halbe Dicke der Balken (b) 10 cm entspricht.

Nach dem Eintragen der vorhandenen Informationen, ergibt sich das in nebenstehender Abbildung eingezeichnete rechtwinklige Dreieck. Mithilfe des Satz des Pythagoras kann nun die Seite c berechnet werden:

\(r^2=b^2+c^2 \\ \Leftrightarrow c=\sqrt{r^2-b^2}\\ \Leftrightarrow c=\sqrt{(40cm)^2-(10cm)^2}\\ \Rightarrow c\approx 38,73 cm\)

Damit ist die gesamte Breite des mittleren Baumstamms (2∙c = b2) etwa 77,5 cm lang.
Nun erfolgt die Berechnung der Breiten der äußeren Balken (b1). Dazu werden wieder die vorhandenen Informationen, also die Dicken der Balken (20 cm = a, a1, a2), die sich daraus ergebende Gesamtdicke dreier Balken (e) und der Durchmesser (d), in der Skizze eingetragen.

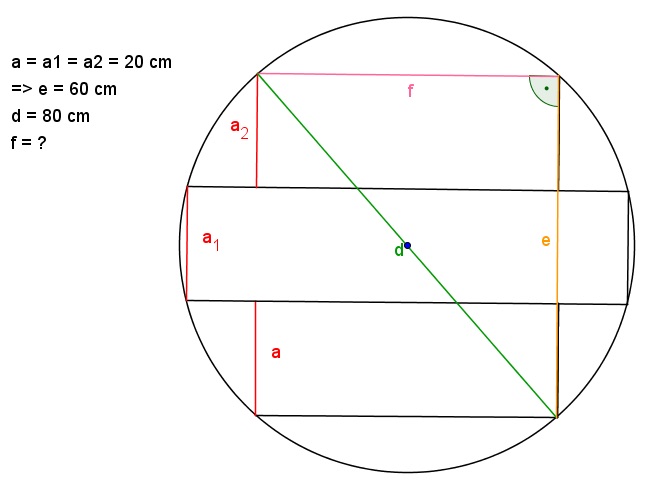So kann die Nutzung des Satzes von Pythagoras zum Herausfinden der Länge von f am entstehenden rechtwinkligen Dreieck (siehe Skizze) leicht durchgeführt werden.

Der Satz des Pythagoras wird angewendet:

\(d^2=e^2+f^2 \\ \Leftrightarrow f= \sqrt{d^2-e^2} \\ \Leftrightarrow f= \sqrt{(80cm)2^-(60cm)^2} \\ \Rightarrow f \approx 52,92cm\)

Damit beträgt die Breite der äußeren Baumstämme (b1) etwa 52,92 cm.          

Zuletzt wird berechnet, wieviel Prozent Abfall anfallen. Der Abfall entspricht der rosa gefärbten Fläche in der Abbildung. Dazu wird zunächst der Flächeninhalt der Schnittfläche des Baumes (Kreisinhalt) berechnet und dann der Flächeninhalt der  Balkenkanten (lila Fläche im blauen Vieleck).

Kreisinhalt:

\(A_K\approx\pi\cdot r^2\\ A_K\approx\pi\cdot(40 cm)^2\\ A_K\approx5026,55 cm^2\)

Flächeninhalt Vieleck:

\(A_V\approx2\cdot a\cdot f + a\cdot g\\ A_V\approx2\cdot 20cm\cdot 52,92cm+20cm\cdot 77,5cm\\ A_V\approx3666,8cm^2\)

Um die Größe der rosa Fläche bzw. des Abfalls herauszubekommen, muss man den Flächeninhalt des Vielecks vom Kreisinhalt abziehen:

\(A_A\approx A_K-A_V\\ A_A\approx 5026,55cm^2-3666,8cm^2\\ A_A\approx 1359,75cm^2\)

Damit entspricht der Abfall einer Fläche von 1359,75 cm2.

Um den prozentualen Anteil des Abfalls an der gesamten Holzmenge zu berechnen, muss die Abfallfläche durch den Kreisinhalt geteilt werden:

\(\frac{1359,75cm^2}{5026,55cm^2}\approx 0,2705\approx27,05\%\)

Ergeben sich also 27,05% Abfall.

Lösungsvariante 2:

Analog könnte man die Seiten b1 und b2 auch über andere rechtwinklige Dreiecke in der Planskizze berechnen. Dazu gehören verschiedene Dreiecke, an denen aufgrund der symmetrischen Verhältnisse der Skizze die Berechnung analog zu der oben beschriebenen stattfinden könnte. Darüber hinaus gäbe es zum Beispiel noch die Möglichkeit b1 über das in dieser Skizze eingezeichnete rechtwinklige Dreieck mit dem Satz des Pythagoras zu berechnen:

\(d^2=a^2+(b_1)^2\\ \Leftrightarrow b_1=\sqrt{d^2-a^2}\\ \Leftrightarrow b_1=\sqrt{(80\;cm)^2-(20\;cm)^2}\\ \Rightarrow b_1\approx 77,56\;cm\)

Ebenso gibt es die Möglichkeit b2 über das in dieser Skizze eingezeichnete rechtwinklige Dreieck mit dem Satz des Pythagoras zu berechnen:

\(r^2=i^2+f^2\\ \Leftrightarrow f=\sqrt{r^2-i^2}\\ \Leftrightarrow f=\sqrt{{40\;cm}^2-{30\;}^2}\\ \Rightarrow f\approx 26,46\;cm\)

\(b_2=2\cdot f\\ b_2\approx2\cdot 26,46\;cm\\ b_2\approx 52,92 \;cm\)

 

Lösungsvariante 3:

Des Weiteren kann man die Aufgabe lösen, indem man Schritt für Schritt die Planskizze in den exakten Größenverhältnissen konstruiert und dann nachmisst bzw. Berechnungen anstellt (zum Beispiel bei GeoGebra).


In der obigen Aufgabe müssen die Schüler sich mit der Geometrie (der Ebene), genauer mit dem Satz des Pythagoras, rechtwinkligen Dreiecken, dem Flächeninhalt des Kreises, des Rechtecks bzw. Vielecks beschäftigen. Hinzu kommt Prozentrechnung bzw. Bruchrechnung. Insgesamt werden sehr viele inhaltsbezogene Kompetenzen, der im Kerncurriculum für das Gymnasium, Jahrgänge 5 bis 10, festgelegten Kompetenzbereiche, angesprochenen: Hinsichtlich des Kompetenzbereiches Zahlen und Operationen am Ende von Schuljahrgang 6 finden sich auf der S. 26 die Anforderungen

Schülerinnen und Schüler

„deuten Dezimalbrüche und Prozentangaben als Darstellungsformen für Brüche und führen Umwandlungen durch“ sowie „nutzen den Prozentbegriff in Anwendungssituationen“.

Bezüglich der Erwartungen zum inhaltsbezogenen Kompetenzbereich Größen und Messen finden sich im Kerncurriculum am Ende von Schuljahrgang 6 (S. 30) die Äußerung

Schülerinnen und Schüler

„schätzen und berechnen Umfang und Flächeninhalt von Rechtecken“

und am Ende von Schuljahrgang 8 (S. 29f.) die Äußerungen

Schülerinnen und Schüler

„berechnen Winkelgrößen mit Hilfe des Thalessatzes und Streckenlängen mit Hilfe des Satzes von Pythagoras“ sowie „schätzen und berechnen Umfang und Flächeninhalt geradlinig begrenzter Figuren“.

Außerdem findet sich am Ende von Schuljahrgang 10 (S. 30) die Kompetenz

Schülerinnen und Schüler

"schätzen und berechnen Umfang und Flächeninhalt von Kreisen“.

Zum Kompetenzbereich Raum und Form steht auf S. 32, dass SuS am Ende von Klasse 8

„den Satz des Thales und den Satz des Pythagoras bei Konstruktionen, Berechnungen und Beweisen“ anwenden sollen.

Zusätzlich findet sich auf S. 34 zum Kompetenzbereich Funktionaler Zusammenhang am Ende der Klassenstufe 6 die Äußerung

Schülerinnen und Schüler

„lösen Grundaufgaben der Prozent- und Zinsrechnung“.

Der Hauptteil der Aufgabe beschäftigt sich mit dem Thema Satz des Pythagoras welcher in der Schulstufe 8 behandelt werden soll. Da aber auch der Kreisinhalt benötigt wird, welcher erst in Schulstufe 9 behandelt werden soll, bietet sich für die Nutzung dieser Aufgabe im Unterricht die Klasse 9 an.


Heuristische Hilfsmittel: 
  • Um die maximalen Breiten in der informativen Figur zu berechnen, sollten SuS zunächst zweckmäßige Bezeichnungen für die im Aufgabentext gegebenen Größen und später für weitere benötigte oder berechnete Angaben einführen. Deutlich leichter fallen die Berechnungen, wenn die Schüler informative Figuren verwenden, also in die bereits gegebene Skizze oder auch neu erstellte Skizzen ihre gegebenen Werte eintragen, um besser nach rechtwinkligen Dreiecken suchen zu können.
  • Außerdem ist das Verwenden von Gleichungen bei der Nutzung des Satzes von Pythagoras und bei der Berechnung des prozentualen Anteils des Abfalls zielführend.
Heuristische Strategien: 
  • Vorwärtsarbeiten, Rückwärtsarbeiten sowie Kombiniertes Vorwärts- und Rückwärtsarbeiten sind sinnvolle Strategien beim Lösen dieser Aufgabe. Immer wieder sollten Schülerinnen und Schüler sich bei den verschiedenen Schritten der Aufgabenbearbeitung fragen, was gegeben ist und was gesucht ist bzw. was sie schon berechnet haben, was sie damit unter Umständen wieder berechnen können usw.
  • Je nachdem, ob im Unterricht schon ähnliche Aufgaben gestellt wurden, können Analogieschlüsse zur Lösungsfindung beitragen. Beispielsweise könnte es sein, dass bereits in früher im Unterricht gestellten Aufgaben, rechtwinklige Dreiecke zunächst „gesucht“ werden mussten, um dann über den Satz des Pythagoras auf das Endergebnis zu kommen.
Heuristische Prinzipien: 
  • In der Lösung obiger Aufgabe findet das Zerlegungs- und Ergänzungsprinzip Anwendung. Die Problemstellung wird umgewandelt, d.h. die Ausgangssituation des Baumstammes mit den gesuchten Längen der maximalen Breiten wird so zerlegt, dass das Problem mit etwas Bekanntem, also dem Satz des Pythagoras, zielführend bearbeitet werden kann.
  • Auf Grund der Symmetrie ist das Symmetrieprinzip auch nuztlich.

Da dieser Aufgabe 6 Punkte vergeben wurden, wurde diese Aufgabe mit *** gekennzeichnet. Hier die Analyse:

Sprachlogische Komplexität: 

Die  Aufgabenstellung besteht aus zwei Hauptsätzen. Obwohl die grobe Struktur (zuerst maximale Breite, dann prozentualen Anteil des Abfalls berechnen) in der Frage vorgegeben wird, entspricht die Reihenfolge der Satzteile nicht unmittelbar den Schritten der mathematischen Bearbeitung, da nicht näher angegeben wird, wie die maximalen Breiten berechnet werden sollen. Eine Vorstellung von dem, was in der Aufgabe gefordert ist, ist jedoch relativ leicht verständlich. Zusätzlich müssen die Inhalte aus dem Text mit der Abbildung in Bezug gesetzt werden. Aufgrund dieser Beobachtungen könnte man die Stufe 1 hinsichtlich der sprachlogischen Komplexität zuordnen.

Kognitive Komplexität: 

Es handelt sich um eine kognitiv recht schwere Aufgabe, denn die Auswahl der Denkvorgänge muss für eine zielgerichtete Aufgabenbearbeitung vor der eigentlichen Bearbeitung stattfinden. SuS können nicht einfach drauf los rechnen, sondern müssen sich zunächst Gedanken machen, wie sie an die gewünschten Ergebnisse gelangen. Dabei sind Vorüberlegungen anzustellen und heuristische, strategische, strukturierende und metakognitive Überlegungen sollten die Bearbeitung begleiten, da eine korrekte Lösung sonst schwer oder nur über Umwege zu erreichen ist. Deshalb ist diese Aufgabe hinsichtlich der kognitiven Komplexität der Stufe 2 zuzuordnen.

Formalisierung von Wissen: 

Zum Lösen der Aufgabe sind in den ersten und zweiten beschriebenen Lösungen einfache formale Darstellungen zu verstehen und teileweise erbringen, weshalb die Aufgabe hinsichtlich der Formalisierung von Wissen bereits der Stufe 1 zuzuordnen ist. Ist eine Lösung durch Konstruktion und Messen (Variante 3) erlaubt, könnte man die Aufgabe jedoch der Stufe 0 zuordnen.

Formelhandhabung: 

Für die ersten zwei beschriebenen Lösungen ist eine höhere Anzahl algebraischer Schritte mit einem ausgewählten, zielgerichteten und kontrollierten Einsatz auszuführen. Deshalb sollte die Aufgabe hinsichtlich der Formelhandhabung die Stufe 2 zugeordnet werden. Hier könnte man aber auch durch Konstruktionen und Messen zur Lösung gelangen, was die Fähigkeit eines Schülers in Form eines Taschenrechners zu arbeiten, unnötig macht und somit das Merkmal der Stufe 0 zugeordnet werden könnte.

Stufenzuordnung: 
Formalisierung von Wissen
Stufe 1
Formelhandhabung
Stufe 2
Kognitive Komplexität
Stufe 2
Sprachlogische Komplexität
Stufe 1

Hilfestellungen: 
Den SuS könnte nicht auf Anhieb klar sein, wie sie die maximalen Breiten berechnen sollen. Unter Umständen könnte es passieren, dass sie die Skizze als maßstabsgetreu annehmen, die dortigen Längen nachmessen und dann nur hochrechnen. Falls sie nicht auf die Idee kommen, den Satz des Pythagoras zu verwenden, könnte man z.B. folgende Hilfestellungen geben:
Allgemein-strategische Hilfen Inhaltsorientierte-strategische Hilfen Inhaltliche Hilfen
Hast du schon mal eine ähnliche Aufgabe bearbeitet? Wie bist du dort vorgegangen? Was hat dir dort geholfen? Sie dir die Skizze genau an. Erkennst du Möglichkeiten, dir bekannte Sätze (über Dreiecke) anzuwenden? Welche Sätze kennst du über rechtwinklige Dreiecke? Kannst du diese hier anwenden?
Kannst du die Bearbeitung der Aufgabe in kleinere Teilschritte untergliedern? An welcher Stelle könnte man gegebene Informationen in der Skizze eintragen, um die Aufgabe leichter lösbar zu machen? Suche rechtwinklige Dreiecke, um den Satz des Pythagoras anzuwenden.
Wie sieht die Anfangssituation aus? Was ist zu tun? Was ist gegeben? Was ist gesucht?   Überlege, an welchen Stellen du den Durchmesser bzw. den Radius gewinnbringend einzeichnen könntest.
 
Veranschauliche dir die Situation.    
 
Weitere Schwierigkeit könnte sein, dass die SuS nicht wissen, wie sie den prozentualen Abfallanteil berechnen sollen. Es könnte auch sein, dass sie zum Beispiel gar nicht darauf kommen, dass es bei dieser prozentualen Berechnung keine Rolle spielt, ob man nun den kompletten Baumstamm (das Volumen) oder nur die Schnittfläche betrachtet. Folgende Hilfestellungen sind u.a. denkbar:
 
Allgemein-strategische Hilfen Inhaltsorientierte-strategische Hilfen Inhaltliche Hilfen
Hast du schon mal eine ähnliche Aufgabe bearbeitet? Wie bist du dort vorgegangen? Hast du alle nötigen Größen bereits berechnet? Ist es nötig, zunächst das Volumen des Baumstammes zu berechnen?
Kannst du die Bearbeitung der Aufgabe in kleinere Teilschritte untergliedern? Welche Größe musst du als Anteil welcher anderen Größe berechnen? Es genügt, den Anteil der Schnittfläche der Balken an der gesamten Schnittfläche der Baumscheibe zu berechnen.
Was ist gegeben? Was ist gesucht?   Wie berechnest du den Anteil der Schnittfläche der Balken bzw. die gesamten Schnittfläche der Baumscheibe?
Veranschauliche dir die Situation.    
Sozialformen: 

Vor allem die Ich-Du-Wir-Methode erscheint sinnvoll. Zunächst kann so individuell eine intensive Auseinandersetzung mit der Aufgabe stattfinden, dann im Partneraustausch die Ideen besprochen und verwirklicht werden. Schließlich können sich die Schüler in kleineren Gruppen besprechen und die Lösungen anschließend vorstellen.

Bei EA besteht die Gefahr, dass vor allem schwächere Schüler gar nicht erst auf Ideen kommen, wie die Aufgabe zielführend zu lösen ist und so die eigentlichen Berechnungen ausbleiben.

Bei reiner GA besteht die Gefahr, dass einzelne vor allem stärkere Schüler die Lösungsidee ihren Mitschülern präsentieren und diese gar nicht erst selbst über eine solche nachdenken.

Eine Besprechung der Aufgabe im Plenum ist sinnvoll, um Fehlvorstellungen zu vermeiden.

Differenzierungsmöglichkeiten: 
Hinweise für die Leistungsschwächeren Schülerinnen und Schüler
  • Schwächeren Schülern, die nicht eigenständig auf Lösungsideen kommen, könnte man an zielführenden Stellen  zum Beispiel den Radius oder den Durchmesser in die Skizze einzeichnen. Noch deutlicher wäre der Hinweis, den Satz des Pythagoras zu nutzen, wenn man rechtwinklige Dreiecke einzeichnet.
  • Weiterhin könnte man vor allem schwächeren Schülern die Möglichkeit geben in einem Konstruktionsprogramm (z.B. GeoGebra), die Skizze selbst nachkonstruieren und am Ende nachmessen zu lassen. Dabei sollten die SuS ihre Schritte erklären können.
Hinweise für die Leistungsstärkeren Schülerinnen und Schüler
  • Leistungsstärkeren Schülern, die schneller fertig sind, könnte man zusätzliche Aufgaben stellen wie beispielsweise:  Wieviel Abfall entsteht, wenn man solche Bretter aus einem 9 m langen Baumstamm heraussägt?
  • Außerdem könnte man ergebnisoffene Arbeitsaufträge formulieren, bei denen die Schüler z.B. das Schnittmuster sinnvoll erweitern sollen, sodass beispielsweise noch Kanthölzer oder ähnliches entstehen.

Die Aufgabe bietet sich an, die Anwendung des Satzes von Pythagoras produktiv zu üben. Als Einstiegsaufgabe ist sie nicht sinnvoll einzusetzen, da die Einsatzmöglichkeit des Satzes erst in der Aufgabe „gesucht“ werden muss. Da in der Aufgabe auch der Kreisinhalt berechnet werden muss, könnte man beispielsweise relativ zu Beginn der Unterrichtseinheit zu Kreisinhalten diese Aufgabe zur Wiederholung des Satzes von Pythagoras sowie zur Verknüpfung mit diesem anwenden.



Bearbeitet von: Ana Kuzle & Janike Wagener
nach oben
712 Nutzer/-innen haben abgestimmt.

Feedback

Wir freuen uns auf Ihre Anregungen und konstruktive Rückmeldung zum Material.