Doppelwürfel I

Fehlermeldung

Deprecated function: The each() function is deprecated. This message will be suppressed on further calls in FieldCollectionItemEntity->fetchHostDetails() (Zeile 313 von /www/htdocs/w0127817/beta.proffi-m.de/sites/all/modules/field_collection/field_collection.entity.inc).
Klasse Schulstufe Thema Themengebiet Schwierigkeit
3/ 4 Primarstufe Würfel Raum und Form **
Heuristsche Hilfsmittel Heuristische Prinzipien Heuristische Strategien
Informative Figur Zerlegungs- und Ergänzungsprinzip, Invarianzprinzip, Symmetrieprinzip Vorwärtsarbeiten, Analogieschlüsse

Aufgabenstellung

 

Aus Zahnstochern und Knetkugeln lassen sich Körper basteln, wie beispielsweise diese Pyramide:

 

 

Wie viele Zahnstocher, wie viele Knetkugeln brauchst du für einen Doppelwürfel?

 

 

 

Quellenangabe:

Original aus Rinkens, H., Rottmann, T., Träger, G. (Hrsg.). (2011). Welt der Zahl (3). Braunschweig: Schroedel. (S. 117)


Zunächst wird definiert, was ein Doppelwürfel ist:

Ein Doppelwürfel ist ein großer Würfel, der einen kleinen Würfel enthält. Dieser kleine Würfel befindet sich im Zentrum des großen Würfels.

 

 

 

 

Lösungsvariante 1 - Zeichnerische Lösung
 

 

Es wird eine Zeichnung von einem Doppelwürfel erstellt.

 

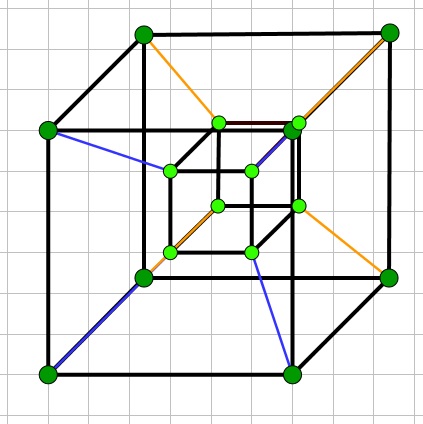
Konstruktionsbeschreibung:

Für den großen Würfel wird eine Kantenlänge von 6 cm gewählt. In das vordere Quadrat des großen Würfels wird dann mit einem Abstand von 2 cm zu allen Seiten ein kleines Quadrat mit der Seitenlänge 2 cm gezeichnet. Dieses kleine Quadrat wird um 1 cm schräg (im 45° Winkel) nach hinten versetzt und die restlichen Seiten des kleinen Würfels werden gezeichnet.
Damit der kleine Würfel im gebauten Modell in dieser Position bleibt, werden weitere Verstrebungen benötigt. Die Eckpunkte des kleinen Würfels werden dementsprechend mit jeweils einem Eckpunkt des großen Würfels verbunden, der in die gleiche Richtung zeigt. Die blauen Verstrebungen stellen die Verbindungen der Ecken der vorderen Quadratflächen  dar, die orangenen Strecken die Verbindungen der Ecken der hinteren Quadratflächen. Zuletzt werden um alle Ecken Kreise, die die Knetkugeln symbolisieren, gezogen. Die Knetkugeln, die die Kanten des großen Würfels zusammenhalten, sind hier dunkelgrün dargestellt, die Knetkugeln, die den kleinen Würfel zusammenhalten, hellgrün.

 

Ermittlung der benötigten Anzahl an Knetkugeln und Zahnstochern:

Im Schrägbild lässt sich nun erkennen, dass insgesamt 16 Knetkugeln benötigt werden. Die Anzahl der Zahnstocher lässt sich nicht einfach durch Abzählen der Kanten ermitteln, da die Kantenlängen des inneren Würfels kleiner sein müssen, als die Kantenlängen des äußeren Würfels.

Der äußere Würfel lässt sich durch 12 Streichhölzer zusammensetzen. Angenommen die Kantenlängen des inneren Würfels sind halb so lang wie die Kantenlängen des äußeren Würfels, dann kann ein innerer Würfel durch 6 Zahnstocher zusammengebaut werden, die jeweils in der Mitte durchgebrochen werden. Weitere 8 Zahnstocher werden für die Verstrebungen benötigt, diese können auf die benötigte Länge zurecht gestutzt werden. Insgesamt werden demnach für die Konstruktion eines Doppelwürfels 26 Zahnstocher benötigt.

 

 

 
 
Lösungsvariante 2 - Rechnerische Lösung

 

 

Ermittlung der Anzahl der Zahnstocher:

Ein Würfel hat 12 Kanten. Da ein Doppelwürfel aus zwei Würfeln besteht hat ein Doppelwürfel 24 Kanten. Die Kanten des inneren Würfel müssen jedoch kleiner sein als die Kanten des äußeren Würfels, da sich ansonsten kein Doppelwürfel basteln lassen würde. Der äußere Würfel lässt sich mit 12 Zahnstochern konstruieren, der innere Würfel würde sich durch Halbierung von 6 Zahnstochern konstruieren lassen.

Außerdem sind die Ecken des inneren Würfels mit der jeweils nächsten Ecke des äußeren Würfels verbunden, sodass sich der innere Würfel genau in der Mitte des äußeren Würfels befindet. Da ein Würfel 8 Ecken hat, gibt es auch 8 Verbindungsstrecken. Die Ecken der Würfel lassen sich durch jeweils einen Zahnstocher verbinden, der entsprechend verkürzt wird. Somit werden für die konstruktion eines Doppelwürfels 12 + 6 + 8 = 26 Zahnstocher benötigt.

 

 

Ermittlung der Anzahl der Knetkugeln:

Ein Würfel hat 8 Ecken. Da ein Doppelwürfel aus 2 Würfeln besteht, werden 2 \(\cdot \) 8 = 16 Knetkugeln benötigt.

 


Die Doppelwürfelaufgabe befindet sich in einem Mathematikbuch für die dritte Klasse. Durch die Analyse der inhaltsbezogenen Kompetenzen (siehe Geförderte Kompetenzen) wird deutlich, dass beim enaktiven Lösungsweg Kompetenzen der Nivaustufe C und beim ikonischen Lösungsweg - wenn es um das Zeichnen eines Schrägbildes geht - sogar Kompetenzen der Niveaustufe D gefördert werden. Laut LISUM (2015) werden Kompetenzen der Niveaustufe C und D von der dritten bis einschließlich zur sechsten Jahrgangsstufe in der Grundschule erworben. Bei der Lösung der Aufgabe soll jedoch nicht die exakte Erstellung eines Schrägbildes im Mittelpunkt stehen, was den Einsatz in der fünften oder sechsten Klasse rechtfertigen würde, sondern eine skizzenhafte Darstellung oder eine enaktive Modellierung genügt für die Aufgabenlösung. Es geht vor allem darum, die Eigenschaften eines Würfels anzuwenden. Demnach eignet sich die Aufgabe besonders für den Einsatz in der dritten oder vierten Klasse im Rahmen der qualitativen Behandlung von Würfeln.

 


Mit der Doppelwürfelaufgabe werden der inhaltsbezogene Kompetenzbereich [L3] Raum und Form sowie die prozessbezogenen Kompetenzbereiche [K2] Probleme mathematisch lösen und [K4] Mathematische Darstellungen verwenden aus dem brandenburgischen Rahmenlehrplan (Teil C) Mathematik für die Jahrgangsstufen 1-10 (LISUM (2015)), der ab dem Schuljahr 2017/18 gültig ist, gefördert. Die geförderten Kompetenzen variieren je nach genutztem Lösungsweg. Daher können und sollen nicht alle nachfolgenden Kompetenzen von jedem Schüler oder jeder Schülerin erreicht werden. Sie stellen nur eine Auswahl möglicher Kompetenzen dar.

 

 

Inhaltsbezogene Kompetenzformulierungen

 

Raum und Form [L3]

Kompetenz 1: Die Schülerinnen und Schüler können Würfel unter Nennung einzelner Merkmale beschreiben.

"Die Schülerinnen und Schüler können ausgewählte geometrische Objekte qualitativ bescheiben" (LISUM, 2015, Geometrische Objekte und ihre Eigenschaften beschreiben, Niveaustufe C, S.26)

Erläuterung: Diese Kompetenzformulierung bezieht sich darauf, dass sich die Schülerinnen und Schüler zur Lösung des Problems auf bekanntes Wissen über einen Würfel beziehen, um davon ausgehend den Doppelwürfel enaktiv, ikonisch oder symbolisch zu konstruieren. Sie benötigen Kenntnisse über Begriffe wie Kanten und Ecken eines Würfels sowie deren Anzahlen, um von diesen auf die Eigenschaften eines Doppelwürfels zu schließen.

 

Kompetenz 2: Die Schülerinnen und Schüler können Kantenmodelle von Würfeln herstellen.

"Die Schülerinnen und Schüler können Modelle ausgewählter Körper herstellen" (LISUM, 2015, Geometrische Objekte darstellen, Niveaustufe C, S.26)

Erläuterung: Wählen Schülerinnen und Schüler den enaktiven Weg und bauen selbst einen solchen Doppelwürfel mithilfe von Zahnstochern und Knete, so erwerben sie die Kompetenz, Kantenmodelle herzustellen.

 

Kompetenz 3: Die Schülerinnen und Schüler können ein Doppelwürfelschrägbild auf Rasterpapier zeichnen.

"Die Schülerinnen und Schüler können geometrische Körper [...] darstellen" (LISUM, 2015, Geometrische Objekte darstellen, Niveaustufe D, S.26)

Erläuterung: Andere (leistungsstärkere) Lernende wählen möglicherweise einen ikonischen Lösungsweg. Dabei können sie lernen und üben, ein Schrägbild eines geometrischen Körpers zu skizzieren.

 

 

Prozessbezogene Kompetenzformulierungen

 

Probleme mathematisch lösen [K2]

Kompetenz 4: Die Schülerinnen und Schüler können die Doppelwürfelaufgabe mithilfe von Kenntnissen über das geometrische Objekt "Würfel" und der Fähigkeit, einen solchen zu modellieren oder darzustellen, lösen.

"Die Schülerinnen und Schüler können mathematische Kenntnisse, Fähigkeiten und Fertigkeiten bei der Bearbeitung von Problemen anwenden" (LISUM, 2015, S.19)

 

Kompetenz 5: Die Schülerinnen und Schüler können Zeichnungen oder Modelle zum Problemlösen nutzen.

"Die Schülerinnen und Schüler [...] nutzen heuristische Hilfsmittel zum Problemlösen anwenden" (LISUM, 2015, S.19) 

 

Erläuterung: Da die Doppelwürfelaufgabe eine Problemlöseaufgabe ist, steht die Kompetenz des „Probleme mathematisch lösen[s]“ im Vordergrund. Die Schülerinnen und Schüler sollten dabei auf ihre eigenen bisherigen Kenntnisse zurückgreifen und sie zur Problemlösung verwenden können. Dabei können sie Lösungsstrategien und heuristische Hilfsmittel anwenden oder neu erlernen. Beispielsweise wäre das Erlernen neuer Strategien und Hilfsmittel durch den Austausch der erarbeiteten Lösungswege in einer Gruppe möglich.

 

Mathematische Darstellungen verwenden [K4]

Kompetenz 6: Die Schülerinnen und Schüler können aus ihren selbst gewählten Darstellungen relevante Aspekte für die Konstruktion eines Doppelwürfels in Hinblick auf die gesuchte Anzahl an Streichhölzern und Knetkugeln ableiten.

"Die Schülerinnen und Schüler können Darstellungen bewerten oder interpretieren." (LISUM, 2015, S.20)

Erläuterung: Bei der Modellierung oder Zeichnung eines Doppelwürfels wird deutlich, dass der innere Würfel kleiner sein muss als der äußere. Somit werden für den innerern Würfel weniger Zahnstocher benötigt als für den äußeren.


Heuristische Hilfsmittel: 
  • Die Aufgabe stellt eine Frage zu einem geometrischen Körper. Daher ist es ein automatischer Impuls sich den Doppelwürfel einmal visuell zu veranschaulichen. Das heuristische Mittel einer informativen Figur ist demnach naheliegend. Jedoch ist beim einfarbigen Skizzieren des Schrägbildes aufgefallen, dass mehrere Verbindungen zweier Ecken genau übereinander liegen, weshalb sie nicht mehr erkennbar waren. Durch farbige Hervorhebungen wurde das Schaubild ein wenig übersichtlicher und die Problematik ansatzweise gelöst. Dennoch lässt sich die richtige Anzahl der Verstrebungen weiterhin nicht auf einen Blick erkennen, sondern bedarf genauerer Betrachtung und richtiger Interpretation der Kanten.

 

 

Heuristische Strategien: 
  • Bei der Lösung der Aufgabe wird in beiden Lösungswegen zunächst das Gegebene betrachtet, nämlich der Doppelwürfel. Es wird geklärt was ein Doppelwürfel ist und überlegt, wie die gesuchten Anzahlen ermittelt werden können. Beim ersten Lösungsweg erfolgt dies letztendlich durch das Erstellen einer Informativen Figur und anschließendes Abzählen der gesuchten Anzahlen. Beim zweiten durch schrittweise Konstruktion eines Doppelwürfels im Kopf. In beiden Lösungswegen wird demnach ausgehend vom Gegebenen hin zum Gesuchten vorwärtsgearbeitet.

 

  • Auch der Analogieschluss ist von Bedeutung, vor allem wenn zuvor eine Aufgabe gestellt wird, in der ein einfaches Würfelmodell gebastelt werden soll (siehe Umsetzung im Mathematikunterricht, Differenzierungsmöglichkeiten). So wissen die Schülerinnen und Schüler das ein einfacher Würfel 8 Ecken hat und ein Doppelwürfel somit doppelt so viele, also 16 Ecken haben muss und damit 16 Knetkugeln benötigt werden. Außerdem hat ein Würfel 12 Kanten ein Doppelwürfel also mindestens doppelt so viele.

 

 

Heuristische Prinzipien: 
  • Bei beiden Lösungswegen wird ein einfacher Würfel zu einem Doppelwürfel ergänzt. Somit spielt das Ergänzungsprinzip eine Rolle. Beim ersten Lösungsweg wird der Doppelwürfel durch Betrachtung der Informativen Figur wieder in seine einzelnen Bestandteile zerlegt, wodurch auch das Zerlegungsprinzip relevant ist.

 

  • Auch das Symmetrieprinzip ist von Bedeutung, da ein Doppelwürfel aus zwei Würfeln besteht, die jeweils die gleiche Anzahl an Kanten und Ecken haben.

 

  • Daneben ist es möglich, dass auch das Invarianzprinzip angewendet wird, wenn die Lernenden den Doppelwürfel mit einem normalen Würfel vergleichen und überprüfen, was die beiden Objekte gemeinsam haben.

Die Doppelwürfelaufgabe hat nach Cohors-Fresenborg et al. unter Berücksichtigung der Lerngruppe einer dritten oder vierten Grundschulklasse eine Schwierigkeit von **.

 

 

Sprachlogische Komplexität: 

Die Sprachlogische Komplexität der Aufgabe lässt sich auf Stufe 1 einordnen, da die Aufgabenstellung aus einfachen Haupt- und Nebensätzen besteht und die Reihenfolge der Sätze und Satzteile keine Hinweise auf die Abfolge der Schritte der mathematischen Bearbeitung gibt.

 

 

Kognitive Komplexität: 

Bei beiden Lösungswegen sind Zusatzüberlegungen über die Länge der einzelnen Kanten eines Doppelwürfels notwendig, um zu einer möglichst realistischen und genauen Gesamtzahl der notwendigen Zahnstocher zu gelangen. Darüber hinaus müssen vor der Bearbeitung der Aufgabe Überlegungen gemacht werden, wie genau vorgegangen werden soll (beispielsweise zeichnerisch oder rechnerisch). In Hinblick auf den Einsatz in einer dritten oder vierten Grundschulklasse entspricht die Aufgabe damit bezüglich der Kognitiven Komplexität der Stufe 2.

 

 

Formalisierung von Wissen: 

Beim ersten Lösungsweg muss lediglich eine Skizze erstellt werden, aus der die gesuchten Anzahlen entnommen werden können, beim zweiten Lösungsweg erfolgt die Lösung rechnerisch. Somit lässt sich die Formalisierung von Wissen auf Stufe 0 ansiedeln.

 

 

Formelhandhabung: 

Die Formelhandhabung entspricht bezüglich beider Lösungswege ebenfalls der Stufe 0. So sind zwar beim rechnerischen Lösungsweg Additionen notwendig, die in Form von Termen aufgeschrieben werden können, Termumformungen sind aber nicht notwendig.

 

 

Stufenzuordnung: 
Formalisierung von Wissen
Stufe 0
Formelhandhabung
Stufe 0
Kognitive Komplexität
Stufe 2
Sprachlogische Komplexität
Stufe 1

Hilfestellungen: 

Bei der Doppelwürfelaufgabe lassen sich einige kritische Stellen identifizieren, bei denen die Schülerinnen und Schüler Schwierigkeiten haben könnten. Die hier aufgezeigten Schwierigkeiten beziehen sich jeweils auf die Bestimmung der Anzahl der für die Konstruktion des Doppelwürfels notwendigen Zahnstocher.

 

Die Schülerinnen und Schüler könnten bei dieser Aufgabe die Vorstellung von einem realen Spiel-Doppelwürfel haben:

                                                                                                                                                                                                 Foto: Marisa Pfläging

Dadurch könnten sie bei ihrer Lösung die Verbindungskanten zwischen den Ecken des inneren und äußeren Würfels vergessen, da diese bei einem realen Doppelwürfel auch nicht vorhanden sind und in einem Zahnstocher-Modell allein der Stabilisierung dienen. Eine solche Schwierigkeit tritt vermutlich eher bei der rechnerischen Lösung auf und es kann als Lehrkraft mit folgenden Hilfestellungen darauf eingegangen werden.

 

Allgemein-strategische Hilfen Inhaltsorientierte strategische Hilfen Inhaltliche Hilfen
Fertige eine Skizze von dem Zahnstocher-Modell an! Stell' dir vor, du bastelst ein solches Modell mit der Anzahl an Zahnstochern, die du berechnet hast! Hast du wirklich alle Verbinungsstrecken zwischen den Knetkugeln berücksichtigt?
Kannst du die Aufgabe auch nicht-rechnerisch lösen?/ Wie kannst du die Aufgabe noch lösen?

Falls die notwendigen Materialien vorhanden sind:

Bastle ein solches Modell mit den von dir herausgefundenen Anzahlen an Knetkugeln und Zahnstochern!

 Was ist ein Doppelwürfel? Welche Eigenschaften hat er?
Stelle dir das Gegebene genau vor! Wäre ein Modell mit der von dir ermittelten Anzahl an Zahnstochern stabil? Sind der äußere und innere Würfel miteinander verbunden?

 

 

Eine weitere Schwierigkeit könnte darin zum Ausdruck kommen, dass die Schülerinnen und Schüler nicht berücksichtigen, dass der innere Würfel eine kürzere Seitenlänge als der äußere Würfel haben muss und dies Einfluss auf die benötigte Anzahl an Zahnstochern haben kann. Kommt es zu diesem Problem, so kann als Lehrperson wie folgt darauf reagiert werden.

 

Allgemein-strategische Hilfen Inhaltsorientierte strategische Hilfen Inhaltliche Hilfen
Fertige eine Skizze an! Vergleiche die Eigenschaften des inneren Würfels mit denen des äußeren Würfels! Wie unterscheiden sich der innere und der äußere Würfel?
Beachte die Eigenschaften eines Doppelwürfels! Achte auf die Seitenlängen der zwei Würfel! Welche Seitenlängen kann der innere Würfel haben?
Es ist auch erlaubt, Zahnstocher durchzubrechen! Lässt sich das Modell basteln, indem nur ganze Zahnstocher verwendet werden? Benötigst du für den inneren Würfel genauso viele Zahnstocher wie für den äußeren Würfel?

 

 

Sozialformen: 
  • Einzelarbeit
  • Partnerarbeit/Gruppenarbeit (Vergleich der Lösungswege)

 

 

Differenzierungsmöglichkeiten: 

Dadurch, dass die Schülerinnen und Schüler den Lösungsweg selbst wählen müssen, lässt sich die Aufgabe gut an das jeweilige Leistungsniveau dieser anpassen. Vor der Bearbeitung der Aufgabe sollte allen Kindern nahegelegt werden, was ein Doppelwürfel ist (siehe Lösung).

 

Für leistungsschwächere Schülerinnen und Schüler können folgende Maßnahmen zur Erleichterung ergriffen werden:

  • Es kann vor dieser Aufgabe eine kleine Einstiegsaufgabe gestellt werden, mit der die Lernenden erste Erfahrungen im Basteln eines Kantenmodells sammeln:
"Baue eine Pyramide. Nimm Zahnstocher für die Kanten und Knetkugeln für die Ecken." (Rinkens, H., Rottmann, T., Träger, G. (Hrsg.). (2011). Welt der Zahl (3). Braunschweig: Schroedel, S. 117)

 

 

 

  • Die Aufgabe kann um einen Aufgabenteil a) ergänzt werden, durch welchen die Kinder zunächst aufgefordert werden, einen einfachen Würfel aus Zahnstochern und Knetkugeln zu basteln. In Aufgabenteil b) kann dann die eigentliche Aufgabe folgen.

 

  • Die Definition eines Doppelwürfels kann um die Information über die acht Verstrebungen ergänzt werden:

"Ein Doppelwürfel ist ein großer Würfel, der einen kleinen Würfel enthält. Der kleine Würfel befindet sich exakt in der Mitte des großen Würfels, wodurch sich bei einem Kantenmodell acht weitere Verstrebungen (Diagonalen) ergeben."

 

Um die Aufgabe an das Niveau leistungsstärkerer Schülerinnen und Schüler anzupassen, können folgende Veränderungen vorgenommen werden:

  • Den Lernenden kann die weitere Aufgabe gestellt werden, mehrere Lösungswege zu finden.

 

  • Die Kinder können den zusätzlichen Auftrag bekommen, weitere Kantenmodelle von Doppelkörpern zu erforschen und eine Regel für die Anzahl der Kanten und Ecken bei Doppelkörpern aufzustellen.

Die Doppelwürfelaufgabe kann vielfältig im Unterricht eingesetzt werden. Zum einen eignet sie sich für die Einführung von Kantenmodellen geometrischer Körper. In diesem Zusammenhang bietet die Doppelwürfelaufgabe eine motivierende und aktivierende Möglichkeit in diesen Bereich einzusteigen. Durch weiterführende Fragen können die Schülerinnen und Schüler auch zu anderen Kantenmodellen oder Regelmäßigkeiten forschen. Gleichzeitig werden dabei Strategien zum Problemlösen entwickelt und geübt. Zum anderen kann die Aufgabe aber auch im Rahmen des Themenbereichs "Geometrische Körper und ihre Eigenschaften" als Übungsaufgabe eingesetzt werden.

Da die Aufgabe einen halboffenen Charakter aufweist (eine Lösung, aber mehrere Lösungswege), können die Lernenden außerdem durch das Vorstellen ihrer Lösungswege das Präsentieren üben.



Bearbeitet von: Sarah Vogel, Michelle Zahn (ergänzt von Marisa Pfläging)
nach oben
584 Nutzer/-innen haben abgestimmt.

Feedback

Wir freuen uns auf Ihre Anregungen und konstruktive Rückmeldung zum Material.