Dreiecke finden

Klasse Schulstufe Thema Themengebiet Schwierigkeit
3/ 4/ 5 Primarstufe Dreiecke Raum und Form, Zahlen und Operationen **

Aufgabenstellung

Diese Figur besitzt ein Stockwerk.

In ihr findet man 6 Dreiecke.

Diese Figur besitzt zwei Stockwerke.

In ihr findet man 12 Dreiecke.
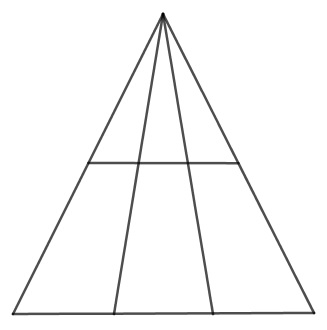
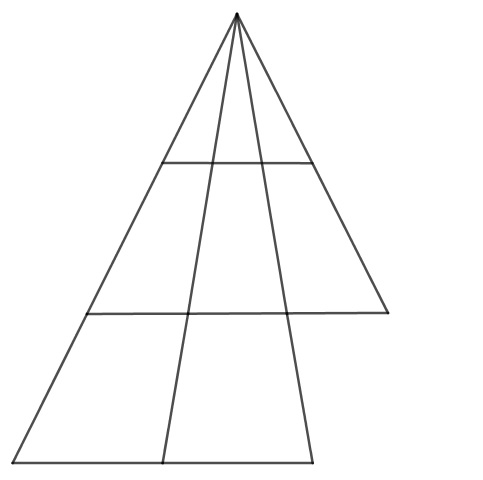
a) Zeichne eine solche Figur mit drei Stockwerken. Wie viele Dreiecke sind in ihr enthalten?

b) Wie viele Dreiecke sind in einer solchen Figur mit 10 Stockwerken zu finden? Begründe.

 

Quellenangabe:

Aufgabenausschuss des Mathematik Olympiaden e.V. (2014). 54. Mathematik-Olympiade 2. Stufe (Regionalrunde). Olympiadeklasse 3. Aufgaben. Abgerufen von http://www.mathematik-olympiaden.de/aufgaben/54/2/A54032.pdf


Lösungsvariante 1 - Lösung durch systematische Schraffierung
 
 
 
a) Es wird zunächst eine Figur mit drei Stockwerken gezeichnet.

 
Alle vorkommenden Dreiecke werden in Einzelskizzen eingezeichnet. Dabei werden die Dreiecke systematisch vom kleinsten zum größten Dreieck (also jeweils von der ersten zur dritten Etage) schraffiert:
 
Anzahl der be-trachteten Etagen

linksgerichtetes spitzes Innendreieck

mittiges spitzes Innendreieck

rechts-gerichtetes spitzes Innendreieck Kombination der linken zwei Innendreiecke Kombination der rechten zwei Innendreiecke Gesamtfläche als Dreieck
1

2

3

 
Es lassen sich somit 18 Dreiecke abzählen.
 
 
b) Bei Betrachtung der Abbildungen in Aufgabenteil a) lässt sich erkennen, dass pro zusätzlicher Etage sechs Dreiecke hinzukommen. Drei neue Dreiecke entstehen durch die Verlängerung der längsgerichteten spitzen Innendreiecke, zwei weitere Dreiecke entstehen aus der Kombination der linken zwei bzw. der rechten zwei längsgerichteten spitzen
Innendreiecke und ein sechstes Dreieck entsteht durch die neue Gesamtfigur. Somit ergibt sich als allgemeine Formel für die Gesamtzahl der Dreiecke \({ A }_{ D }\) für ein Dreieck mit \(x\) Etagen:
 
  \({ A }_{ D }(x)=6\cdot x=6x\)
\(\Rightarrow \) \({ A }_{ D }(10)=6\cdot 10\)
\(\Leftrightarrow \) \({ A }_{ D }(10)=60\)
 
 
In einer Figur mit 10 Stockwerken sind 60 Dreiecke zu finden.
 

 

 

Lösungsvariante 2 - Lösung durch systematische Ergänzung

 
 
a) Es wird von der Figur aus Aufgabenteil b) ausgegangen.

 

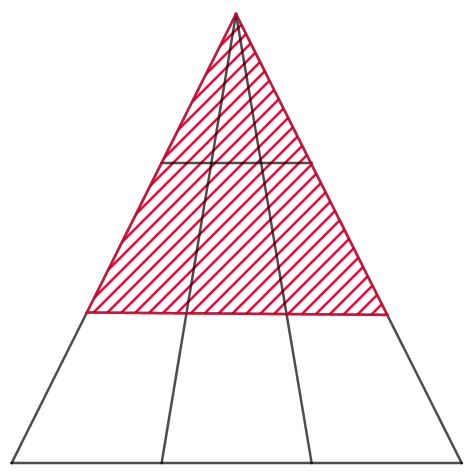
Dieses zweietagige Dreieck wird nun systematisch um Linien ergänzt, sodass letztendlich ein Dreieck mit drei Etagen entsteht:

  Ausgangsfigur Ergänzungsschritt 1 Ergänzungsschritt 2 Ergänzungsschritt 3
Figur

 

hinzuge-kommene Dreiecke -

      
Anzahl der Dreiecke 12 12+1=13 13+2=15 15+3=18
 
In einer dreistöckigen Figur sind somit 18 Dreiecke enthalten.
 
 
b) Aus den in der Aufgabenstellung gegebenen Dreiecksanzahlen der jeweiligen Figuren sowie der in Aufgabenteil a) ermittelten Anzahl an Dreiecken in einer dreistöckigen Figur lässt sich eine Tabelle anlegen:  
 
Anzahl der Stockwerke Anzahl der Dreiecke
1 6
2 12
3 18

 

Es lässt sich erkennen, dass pro Stockwerk eine Etage hinzukommt:
 
  Anzahl der Stockwerke Anzahl der Dreiecke  
  1 6  
2 12
3 18
 
 
Durch Weiterführen der Tabelle lässt sich auch die Anzahl an Dreiecken in einer zehnstöckigen Figur ermitteln:
 
  Anzahl der Stockwerke Anzahl der Dreiecke  
  1 6  
2 12
3 18
4 24

...

...
   
   
10 60

 

Es lässt sich erkennen, dass sich die Anzahl an Dreiecken \({ A }_{ { D }_{ 10 } }\) in einer zehnstöckigen Figur wie folgt berechnen lässt:

\({ A }_{ { D }_{ 10 } }=6+6+...+6=10\cdot 6\)
                                  

 

In einer Figur mit 10 Stockwerken sind also 60 Dreiecke zu finden.
 

Die Aufgabe kann ab der dritten Jahrgangsstufe eingesetzt werden, da dann bereits alle notwendigen Vorkenntnisse (Sachwissen über Dreiecke und Strecken, Beherrschen des kleinen 1x1, zeichnerische Fertigkeiten zur Erstellung geometrischer Figuren) vorhanden sein sollten. Die Herausforderung liegt in der Teilaufgabe b), die voraussichtlich nur leistungsstärkere Drittklässlerinnen und Drittklässler meistern dürften. Die Beschreibung und Begründung des Zusammenhangs zwischen der Anzahl der Stockwerke und der Anzahl der Dreiecke in der Figur erfordern Fähigkeiten des Problemlösens und der mathematischen Kommunikation, die eher in der vierten und fünften Klasse zu erwarten sind.


Die Aufgabe berührt die prozessbezogenen Kompetenzbereiche „[K1] mathematisch argumentieren“, „[K2] Probleme mathematisch lösen“, „[K5] mathematische Darstellungen verwenden“ und „[K6] mathematisch kommunizieren“ sowie die inhaltsbezogenen Kompetenzbereiche „[L3] Raum und Form“ und ferner auch „[L1] Zahlen und Operationen“ des brandenburgischen Rahmenlehrplans (Teil C) Mathematik für die Jahrgangsstufen 1-10 (LISUM (2015)), der ab dem Schuljahr 2017/18 gültig ist.

 

 

Inhaltsbezogene Kompetenzformulierungen

 

Raum und Form [L3]

Kompetenz 1: Die Schülerinnen und Schüler skizzieren eine komplexe ebene Figur mit vorgegebenen Eigenschaften.

"Zeichnen ebener Figuren frei Hand und mithilfe von Zeichengeräten (Lineal, Geodreieck, Zirkel) überwiegend auf Blankopapier" (LISUM (2015), Geometrische Objekte darstellen, Niveaustufe C, S.46)

 

Kompetenz 2: Die Schülerinnen und Schüler erkennen und benennen Dreiecke innerhalb einer komplexen ebenen Figur.

"Erkennen, Benennen und Beschreiben ebener Figuren (auch Parallelogramm, Trapez, Drachenviereck, Raute) in der Umwelt und am Modell [...]" (LISUM (2015), Geometrische Objekte und ihre Eigenschaften beschreiben, Niveaustufe C, S.46)

 

Zahlen und Operationen [L1]

Kompetenz 3: Die Schülerinnen und Schüler verknüpfen Additions- und Malaufgaben miteinander und setzen diese strategisch ein.

"Die Schülerinnen und Schüler können Rechenstrategien, -verfahren, -regeln und Gesetze der Grundrechenoperationen im Bereich der natürlichen Zahlen bis 1 Million situationsangemessen nutzen" (LISUM (2015), Rechenverfahren und -strategien anwenden, Niveaustufe C, S.23)

 

 

Prozessbezogene Kompetenzformulierungen

 

Mathematisch argumentieren [K1]

Kompetenz 4: Die Schülerinnen und Schüler erkennen die regelmäßige Zunahme der Dreiecksanzahl in der gegebenen geometrischen Figur in Abhängigkeit der Anzahl der Stockwerke dieser Figur.

"Die Schülerinnen und Schüler können Zusammenhänge und Strukturen erkennen und Vermutungen zu mathematischen Situationen aufstellen" (LISUM (2015), S. 19)

Erläuterung: Um Teilaufgabe b) lösen zu können, müssen die Schülerinnen und Schüler den regelhaften Zusammenhang zwischen der Zahl der Dreiecksstockwerke und der Zahl der Dreiecke erkennen und diese Struktur schriftlich beschreiben.

 

Probleme mathematisch lösen [K2]

Kompetenz 5: Die Schülerinnen und Schüler finden einen Lösungsweg, um die Anzahl der Dreiecke in einer komplexen geometrischen Figur zu ermitteln.

"Die Schülerinnen und Schüler können Aufgaben bearbeiten, zu denen sie noch keine Routinestrategie haben." (LISUM (2015), S.19)

Erläuterung: Das Aufgabenformat (insb. Teilaufgabe b) dürfte den meisten Lernenden unbekannt sein - wie es für die Aufgaben der Mathematikolympiade typisch ist. Sie verfügen also nicht über eine Routinestrategie beim Lösen. Gleichwohl ist ihnen das notwendige Wissen zur Lösung der Aufgabe, insbesondere Wissen über die Eigenschaften von Dreiecken, bekannt und sie sind nun gefordert, dieses Wissen strategisch anzuwenden.

 

Kompetenz 6: Die Schülerinnen und Schüler fertigen eine Skizze zur Aufgabe an.

"Die Schülerinnen und Schüler können heuristische Hilfsmittel zum Problemlösen anwenden." (LISUM (2015), S.19)

Erläuterung: Zur Lösung von Teilaufgabe b) bietet es sich an, mit Skizzen und/oder einer Tabelle zu arbeiten, um den Zusammenhang zwischen der Zahl der Stockwerke und Zahl der Dreiecke systematisch untersuchen zu können. Die Aufgabe dürfte nicht allein durch Nachdenken zu lösen sein, sodass sie für die Anwendung von Heurismen sehr geeignet ist.


Heuristische Hilfsmittel: 
  • Bei beiden Lösungswegen werden mehrere Skizzen der Dreiecksfigur gezeichnet und dahingehend verändert, dass eine Regelhaftigkeit für den Zuwachs an Dreiecken bei Hinzufügen eines Dreiecks deutlich wird. Das Anfertigen einer Skizze bietet sich bei dieser Aufgabe besonders an, weil es einerseits direkt gefordert wird und den Schüler, bzw. die Schülerin somit auf seine Sinnhaftigkeit aufmerksam macht, und Skizzen andererseits insbesondere bei Aufgaben der ebenen Geometrie sehr sinnvoll sind, weil sie die Schülerinnen und Schüler zeichnerisch meist noch nicht überfordern (wie etwa 3D-Abbildungen) und gleichzeitig bei der räumlichen Vorstellung sowie bei der Operation mit den ebenen Figuren helfen.

 

  • Beim zweiten Lösungsweg von Aufgabenteil b) wird eine Tabelle mit der Anzahl an Dreiecken in Abhängigkeit von der Anzahl an Stockwerken erstellt. Mithilfe dieser werden weitere Dreiecksanzahlen bestimmt und es wird vielleicht sogar ein allgemeiner Zusammenhang erkannt. 

 

  • Auch Gleichungen werden insbesondere bei der ersten Lösungsvariante genutzt: Hier wird eine allgemeine Formel zur Berechnung der Dreieckanzahl in Abhängigkeit von der Etage aufgestellt.

 

 

Heuristische Strategien: 
  • Insbesondere die Strategie des Systematischen Probierens ist für die Lösung von Bedeutung. So wird überlegt, wie systematisch alle Dreiecke in der dreistöckigen Figur identifiziert werden können. Dabei wird nach Zusammenhängen innerhalb des Problems (hier: zwischen Figuren mit einer unterschiedlichen Zahl an Stockwerken) gesucht und diese werden schließlich für die Lösung der Teilaufgabe b) genutzt.

 

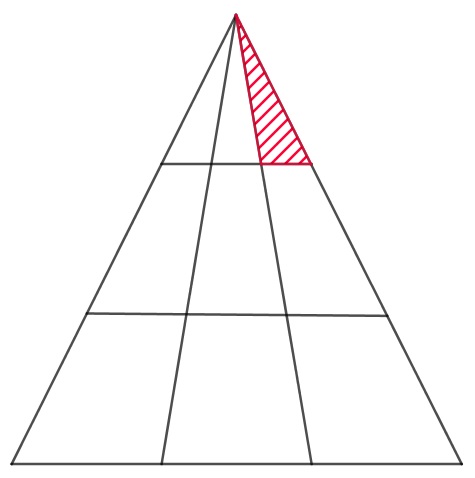
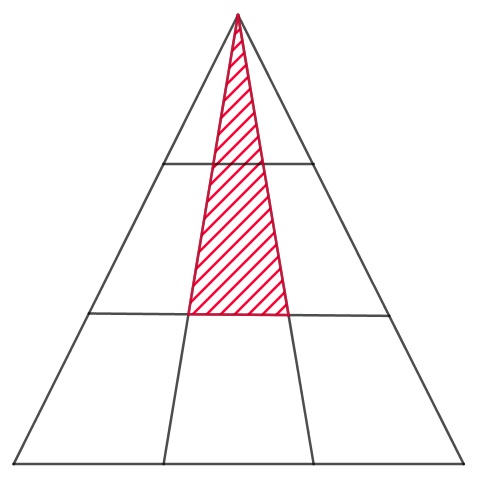
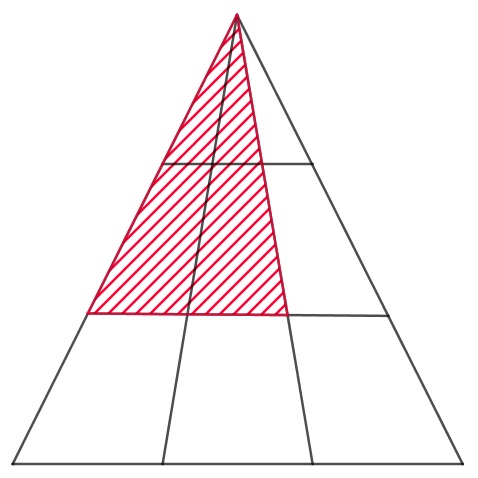
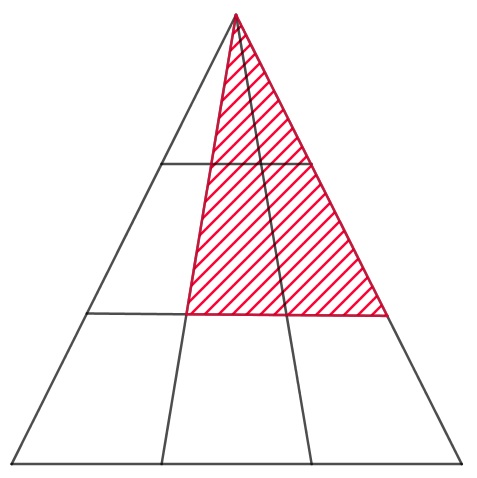
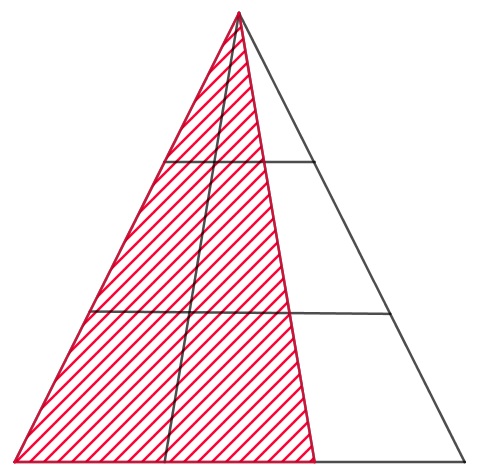
  • Dabei wird bei Teilaufgabe a) vorwärts gearbeitet: Beim ersten Lösungsweg wird die dreistöckige Figur betrachtet und es wird mithilfe von Skizzen, durch Schraffieren aller möglichen Dreiecke und schließlich durch das Abzählen dieser zum Gesuchten gelangt. Beim zweiten Lösungsweg wird die zweistöckige Figur betrachtet und durch Ergänzen dieser und paralleles Abzählen der hinzugekommenen Dreiecke wird die Gesuchte Anzahl an Dreiecken ermittelt. Auch hier wird demnach vorwärts gearbeitet. Bei der Lösung von Aufgabenteil b) wird beim zweiten Lösungsweg vorwärts gearbeitet (die Tabelle wird bis zur zehnstöckigen Figur ergänzt). Bei der ersten Lösungsvariante wird kombiniert vorwärts und rückwärts gearbeitet, so wird zunächst das Gesuchte betrachtet und das Teilziel gesetzt, eine allgemeine Berechnungsformel für die Anzahl der Dreiecke in Abhängigkeit von der Etagenzahl zu ermitteln. Beim Aufstellen dieser Formel wird vorwärts gearbeitet und dann wird wieder das Gesuchte betrachtet, die Stockwerkzahl 10 in die Formel eingesetzt und die gesuchte Dreiecksanzahl berechnet.    

 

 

Heuristische Prinzipien: 
  • Insbesondere bei der ersten Lösungsvariante von Teilaufgabe a) wird das Zerlegungsprinzip verwendet, da die Teildreiecke der dreistöckigen Figur schraffiert werden. Beim zweiten Lösungsweg dieser Aufgabe wird die zweistöckige Figur schrittweise ergänzt und somit das Ergänzungsprinzip angewandt.

 

  • Auch das Invarianzprinzip ist bei Teilaufgabe a) von Bedeutung. So wird beim ersten Stockwerk begonnen und von Stockwerk zu Stockwerk betrachtet, welche Dreiecke gleich bleiben und welche hinzukommen. Dies ist auch bei der zweiten Lösungvariante dieser Aufgabe der Fall: Es wird betrachtet, welche Dreiecke der zweistöckigen Figur existieren und durch welche diese Figur zur dreistöckigen Figur ergänzt wird.

 

  •  Ein weiteres relevantes Prinzip ist das Symmetrieprinzip. Dieses wird bei Teilaufgabe b) angewandt. So wird dort verglichen, welche Zusammenhänge zwischen den Dreieckszahlen von Figuren mit verschieden Stockwerkzahlen bestehen und die Schülerinnen und Schüler erkennen, dass es sich um einen konstanten Zuwachs von sechs Dreiecken handelt. Es besteht somit die Analogie, dass dieser Zuwachs von Stockwerk zu Stockwerk gleich ist.  

Die Aufgabe "Dreiecke finden" hat nach Cohors-Fresenborg et al. bezüglich beider dargestellten Lösungswege einen Schwierigkeitsgrad von **.

 

 

Sprachlogische Komplexität: 

Die Aufgabenstellung besteht aus einfachen Hauptsätzen. In Aufgabenteil a) entspricht die Reihenfolge der Sätze der mathematischen Bearbeitungsschritte, so ist es durch den Arbeitsauftrag naheliegend zunächst ein dreistöckiges Dreieck zu zeichnen und dann die vorhandenen Dreiecke abzuzählen. Aufgabenstellung b) gibt jedoch keine Hinweise auf die Bearbeitungsschritte. Somit entspricht die Sprachlogische Komplexität der Aufgabe der Stufe 1.

 

 

Kognitive Komplexität: 

Bei Aufgabenteil b) kann es sinnvoll sein das Heuristische Hilfsmittel der Tabelle zu nutzen, um einen Zusammenhang zwischen dem Stockwerk und der zugehörigen Anzahl der Dreiecke zu erkennen. Denkvorgänge müssen demnach der Bearbeitung der Aufgabe vorangehen und somit lässt sich die Aufgabe in Anbetracht einer dritten bis fünften Grundschulklasse auf Stufe 2 ansiedeln.

 

 

Formalisierung von Wissen: 

Beim ersten Lösungsweg ist das Aufstellen einer Gleichung erforderlich, um die Anzahl an Dreiecken bei zehn Stockwerken zu bestimmen. Beim zweiten Lösungsweg ist eine Gleichung ebenfalls sinnvoll, aber nicht zwingend notwendig, da die Aufgabe auch nur durch eine zehnzeilige Tabelle gelöst werden könnte. Somit lässt sich die Formalisierung von Wissen bezüglich des ersten Lösungsweges in Hinblick auf eine Grundschulklasse auf Stufe 1 einordnen und bezüglich des zweiten Lösungsweges auf Stufe 0.

 

 

Formelhandhabung: 

Bei beiden Lösungswegen muss lediglich addiert und/oder multipliziert werden. Beim ersten Lösungsweg muss eine Gleichung aufgestellt werden, in die für eine Variable eine Zahl eingesetzt wird. Beim zweiten Lösungsweg werden lediglich Rechenoperationen durchgeführt, die aber nicht in Form von allgemeinen mathematischen Gleichungen dokumentiert werden. Somit lässt sich auch die Formelhandhabung der Aufgabe "Dreiecke finden" bezüglich des ersten Lösungsweges in Hinblick auf eine Grundschulklasse auf Stufe 1 ansiedeln und bezüglich des zweiten Lösungsweges auf Stufe 0.

 

 

Stufenzuordnung: 
Formalisierung von Wissen
Stufe 0
Stufe 1
Formelhandhabung
Stufe 0
Stufe 1
Kognitive Komplexität
Stufe 2
Sprachlogische Komplexität
Stufe 1

Hilfestellungen: 

Bei der Bearbeitung der Aufgabe durch die Schülerinnen und Schüler können an einigen Stellen des Problemlöseprozesses Schwierigkeiten auftreten. Hier werden zwei dieser kritischen Stellen dargestellt und es wird aufgeführt, welche allgemein-strategischen, inhaltsorientierten strategischen und inhaltlichen Hilfen in solchen Fällen weiterhelfen können.

 

Die Lernenden könnten Probleme dabei haben, verschiedene sich überschneidende Dreiecke zu identifizieren, und daher nicht alle Dreiecke finden. In diesem Fall können folgende Hinweise gegeben werden.

Allgemein-strategische Hilfen Inhaltsorientierte strategische Hilfen Inhaltliche Hilfen
Markiere die verschiedenen Dreiecke in deiner Skizze mit verschiedenen Farben. Gibt es Linien die du "ausblenden" könntest? Es macht nichts, wenn ein Dreieck durch weitere Linien unterteilt wird.
Fertige ruhig mehrere Skizzen an. Welche Dreiecke könntest du aus der dreistöckigen Figur herausschneiden? Vielleicht hilft es dir, wenn du dir mehrere Ebenen vorstellst, in denen sich jeweils ein Dreieck befindet. Diese Ebenen und damit auch die Dreiecke können übereinander liegen.
Welche 12 Dreiecke lassen sich in der zweistöckigen Figur finden? Wie bist du dort vorgegangen? Welche Dreiecke aus einer Figur lassen sich durch Hinzufügen eines Stockwerkes an die Figur vergrößern? Welche Dreiecke überschneiden sich?

 

 

Des Weiteren könnten die Schülerinnen und Schüler bei der Bearbeitung von Aufgabenteil b) nicht auf die Idee kommen, dass es ihnen Arbeit erleichtern würde, wenn sie einen allgemeinen Zusammenhang zwischen der Anzahl der Stockwerke und der Anzahl der Dreiecke finden. Kann diese Barriere von den Kindern nicht eigenständig überwunden werden, so können folgende Hinweise weiterhelfen.

Allgemein-strategische Hilfen Inhaltsorientierte strategische Hilfen Inhaltliche Hilfen
Können dir die gegebenen Informationen und der in Aufgabenteil a) ermittelte Wert hilfreich sein? Vergleiche die Zahl der Dreiecke bei verschieder Zahl an Stockwerken. Was fällt dir auf? Wie verändert sich die Anzahl an Dreiecken, wenn ein Stockwerk hinzugefügt wird?
Nutze eine Tabelle! Wie hättest du die Anzahl an Dreiecken in der zweistöckigen und dreistöckigen Figur jeweils auch berechnen können? Finde eine Berechnungsformel zur Berechnung der Anzahl der Dreiecke bei 10 Stockwerken.
Du kannst Aufgabenteil b) auch rechnerisch lösen. Gibt es eine Regel für den Zuwachs an Dreiecken bei Erhöhung der Stockwerke? -

 

 

 

Sozialformen: 
  • Einzelarbeit
  • Vergleich der Aufgabe in Partnerarbeit möglich

 

 

Differenzierungsmöglichkeiten: 

Aufgabenteil a) ist deutlich einfacher zu lösen als b). Letzterer könnte daher als Zusatzaufgabe für leistungsstärkere Schülerinnen und Schüler gekennzeichnet werden. Neben dieser Differenzierung können weitere Maßnahmen ergriffen werden, damit der Anspruch der Aufgabe sowohl für leistungsschwächere als auch für leistungsstärkere Schülerinnen und Schüler angemessen ist.

 

Differenzierungsmöglichkeit für leistungsstärkere Schülerinnen und Schüler:

  • Es kann die Zusatzaufgabe gestellt werden: "Wie viele Vierecke sind in einer solchen Figur mit 10 Stockwerken zu finden?

 

Differenzierungsmöglichkeit für leistungsschwächere Schülerinnen und Schüler:

  • Es könnte ein heuristischer Lösungsweg vorgeschlagen und evtl. bereits auf dem Aufgabenblatt skizziert werden (z.B. Tabelle).

Die Aufgabe eignet sich zum produktiven Üben. Sie schult die logische Denkfähigkeit der Kinder, eignet sich zum Ausprobieren, Vergleichen und Üben heuristischer Strategien bei Problemlöseaufgaben und trainiert das räumliche Vorstellungsvermögen (insbesondere die Figur-Grund-Wahrnehmung).



Bearbeitet von: Friederike Michalek (ergänzt von Marisa Pfläging)
nach oben
441 Nutzer/-innen haben abgestimmt.

Feedback

Wir freuen uns auf Ihre Anregungen und konstruktive Rückmeldung zum Material.