Formen-Puzzle

Fehlermeldung

Deprecated function: The each() function is deprecated. This message will be suppressed on further calls in FieldCollectionItemEntity->fetchHostDetails() (Zeile 313 von /www/htdocs/w0127817/beta.proffi-m.de/sites/all/modules/field_collection/field_collection.entity.inc).
Klasse Schulstufe Thema Themengebiet Schwierigkeit
6 Primarstufe Kongruenzabbildungen (genauer: Parkettierung) Raum und Form **

Aufgabenstellung

In einem Puzzle gibt es acht verschiedene, rechtwinklige, flächengleiche Formen, die jeweils acht Kästchen umfassen. Von jeder Form sind ausreichend Teile vorhanden, die auch gedreht und umgeklappt verwendet werden dürfen.

 

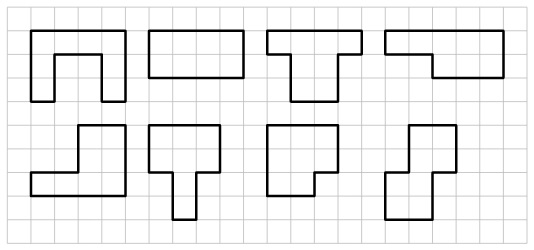
a) Ein Quadrat (8∙8 Kästchen) soll mit Teilen einer einzigen Form vollständig ausgelegt werden (Parkettierung).

Zeichne zwei verschiedene Möglichkeiten mit unterschiedlichen Formen.

 

b) Nun soll ein Quadrat (8∙8 Kästchen) mit Teilen zweier verschiedener Formen ausgelegt werden; sie müssen nicht in der gleichen Anzahl vorkommen.

Zeichne vier Möglichkeiten, die sich untereinander jeweils in mindestens einer der verwendeten Formen unterscheiden.

 

c) Schließlich soll ein Quadrat (8∙8 Kästchen) mit Teilen aus vier verschiedenen Formen ausgelegt werden; sie müssen nicht in der gleichen Anzahl vorkommen.

Zeichne zwei Möglichkeiten, die nicht in allen vier verwendeten Formen Übereinstimmen.

 

 

Quellenangabe:

Aufgabenausschuss des Mathematik-Olympiaden e.V. (2011). 50. Mathematik-Olympiade. 3. Stufe (Landesrunde). Klasse 6, Aufgaben - 1. Tag. (http://www.mathematik-olympiaden.de/archiv.html. Letzter Zugriff: 30. Dezember 2016.)


Ausgangsformen:

 

 

 

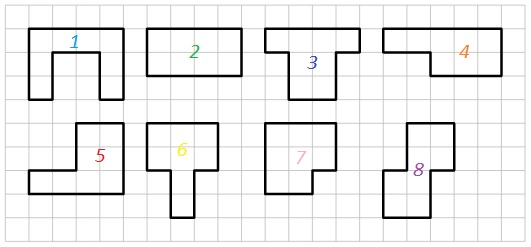
Lösungsvariante 1 - Lösung durch Systematisches Ausprobieren/Puzzeln im Kopf

 

Grundüberlegung: Die Formen werden der Reihe nach durchgegangen und es wird ausprobiert, ob sie sich zu einem 8∙8 Kästchen großen Quadrat zusammensetzen lassen.

 

Aufgabenteil a)

  • Es wird bei Form 1 begonnen. Durch Ausprobieren (ggf. Anfertigen von Skizzen) lässt sich feststellen, dass ein Quadrat mit 8∙8 Kästchen nicht vollständig durch die erste Figur parkettiert werden kann.

 

  • Mit der zweiten Figur gelingt dies allerdings:

 

 

 

  • Ein Auslegen des 8∙8 Kästchen großen Quadrats mit der dritten Form gelingt nicht.

 

  •  Mit der vierten Form lässt sich das Quadrat jedoch parkettieren:

 

 

 

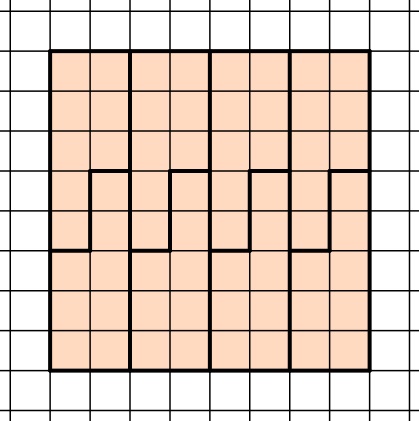
Somit wurden zwei Möglichkeiten, das 8∙8 Kästchen große Quadrat mit einer einzigen Form zu parkettieren, gezeichnet.

 

 

Aufgabenteil b)

  • Wähle Form 1 und Form 2. Es ergibt sich durch Ausprobieren folgende Parkettierung:

 

 

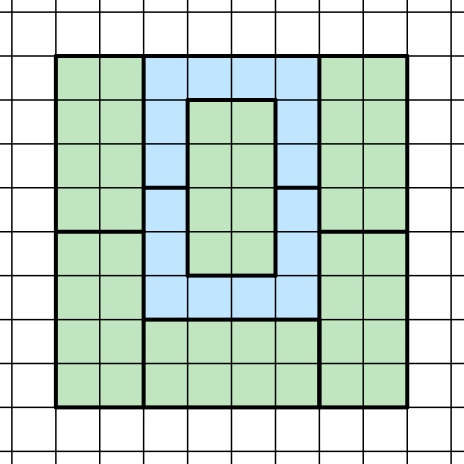
Die zwei Formen müssen laut Aufgabenstellung nicht in der gleichen Anzahl vorkommen, somit ist hiermit eine erste Möglichkeit der Parkettierung gefunden.

 

  • Die verwendeten Formen sollen sich laut Aufgabenstellung bei Angabe der Möglichkeiten in mindestens einer der Formen unterscheiden, wähle nun also die erste und die dritte Form. Es lässt sich direkt erkennen, dass sich die beiden Formen zu einem 4∙4 Kästchen großen Quadrat zusammensetzen lassen:

 

 

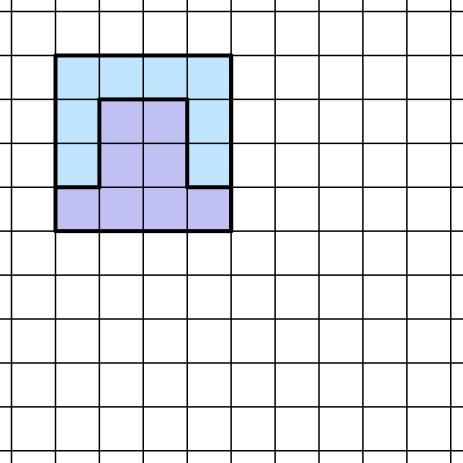
Somit lässt sich mit diesen Formen durch viermaliges Aneinanderreihen des 4∙4 Kästchen großen Quadrats auch ein 8∙8 Kästchen großes Quadrat parkettieren:

 

 

 

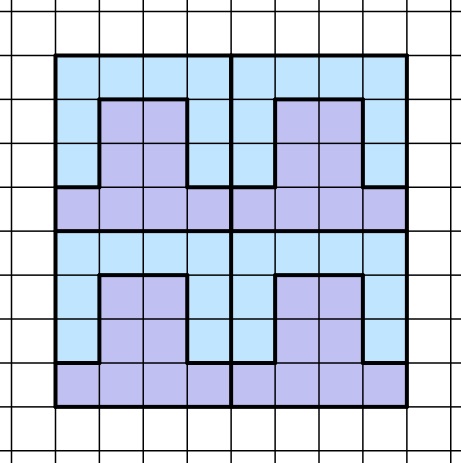
  • Bei der Wahl von Form 1 und Form 4, Figur 1 und Figur 5, Figur 1 und Figur 6 sowie von Form 1 und Form 7 lässt sich die 8∙8 Kästchen große Fläche jeweils nicht auslegen.

 

  • Mit der ersten und der achten Form gelingt dies jedoch wieder. Zunächst ist ersichtlich, dass sich mit diesen beiden Formen ein 4∙8 Kästchen großes Rechteck auslegen lässt:

 

 

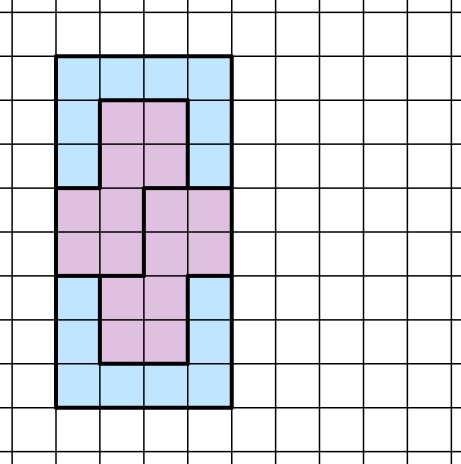
Durch zweimaliges Aneinanderlegen dieses Rechtecks lässt sich mit den beiden Formen also ein 8∙8 Kästchen großes Quadrat parkettieren:

 

 

 

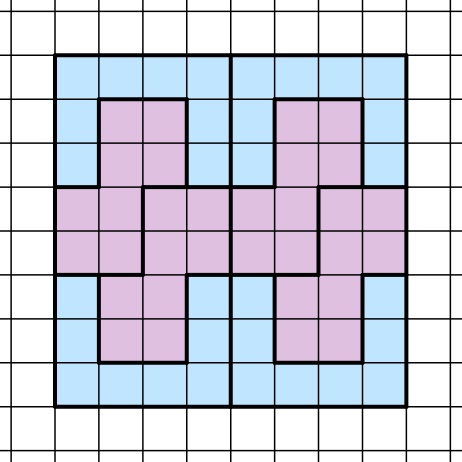
  • Wähle nun die zweite und die dritte Form. Eine Parkettierung gelingt damit nicht.

 

  • Mit der zweiten und vierten Form lässt sich das 8∙8 Kästchen große Quadrat aber wieder auslegen:

 

 

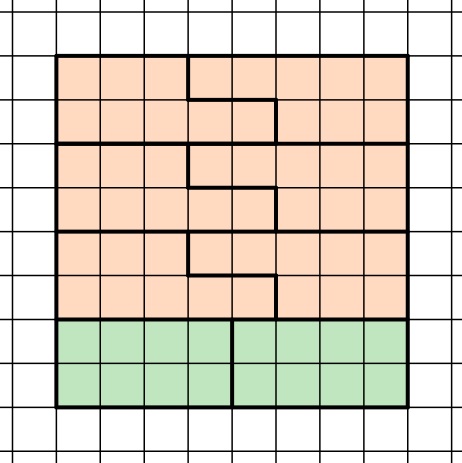
Bei dieser Möglichkeit kann die Anzahl der zweiten und vierten Form variiert werden. Es wären auch andere Parkettierung (4x Form 2 & 4x Form 4, 6x Form 2 &  2 x Form 4) möglich, da eine zweifache Auslegung jeder Form jeweils ein 2∙8 Kästchen großes Rechteck ergeben kann und sich diese Rechtecke jeweils durch einander ersetzen lassen.

 

Somit wurden vier verschiedene Möglichkeiten der Parkettierung des 8∙8 Kästchen großen Quadrats mit zwei verschiedenen Formen angegeben.

 

 

Aufgabenteil c)

  • Wähle die Figuren 1, 2, 3 und 4. Das 8∙8 Kästchen große Quadrat lässt sich durch einmaliges Auslegen der ersten Form, viermaliges Auslegen der zweiten Form, einmaliges Auslegen der dritten Form und zweimaliges Auslegen der vierten Figur parkettieren:

 

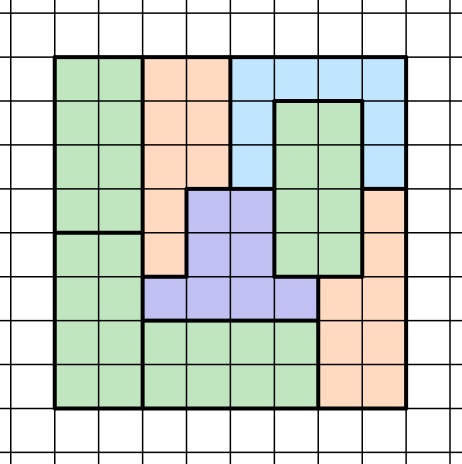
Auch in diesem Aufgabenteil müssen die Formen nicht in gleicher Anzahl vorkommen, somit ist hiermit eine erste Möglichkeit der Plakettierung mit vier verschiedenen Formen gefunden worden.

 

  • Eine weitere Möglichkeit ergibt sich durch vierfache Auslegung der zweiten Form, eine fünfte Form, eine sechste Form und zweifache Auslegung der siebten Form:

 

 

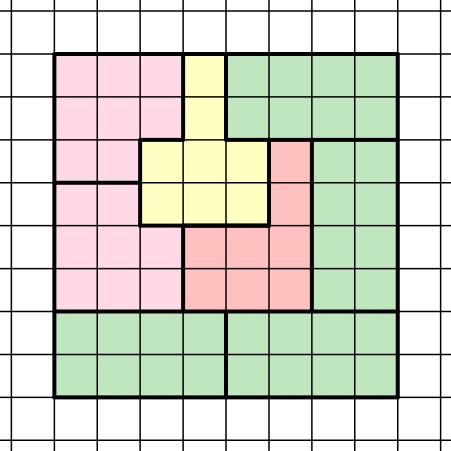
Laut Aufgabenstellung sollen die Lösungen nicht in allen vier Formen übereinstimmen. Da in den beiden Parkettierungen nur die zweite Form übereinstimmt, ist diese Bedingung erfüllt.

 

Somit wurden hier zwei verschiedene Möglichkeiten der Parkettierung des 8∙8 Kästchen großen Quadrats mit jeweils vier verschiedenen Formen angegeben.

 

 

 

Lösungsvariante 2 - Lösung durch genaue Untersuchung der Seitenlängen der Figuren

 

Grundüberlegung: Es wird das zu parkettierende Quadrat betrachtet, dessen Seiten jeweils einer Länge von acht aneinandergereihten Kästchen entsprechen.

Definiere: 1 Kästchen := 1 Längeneinheit (LE)

Die Teiler von 8 sind 1, 2, 4 und 8. Die Formen können also unter dem Gesichtspunkt betrachtet werden, ob sich die Formen so zu Rechtecken zusammensetzen lassen, dass die Seitenlängen dieser erzeugten Rechtecke einer dieser Teiler entsprechen, und sich das 8∙8 Kästchen große Quadrat wiederum aus diesen Rechtecken zusammensetzen lässt.

 
 
Aufgabenteil a)
 

I. Bei Betrachtung der Formen fällt direkt auf, dass die zweite Figur ein Rechteck der Seitenlängen 2 LE und 4 LE ist. Das 8∙8 Kästchen große Quadrat lässt sich somit aus acht dieser Figuren zusammensetzen, denn 8:2=4, 8:4=2 und 2∙4=8.

 

 

 

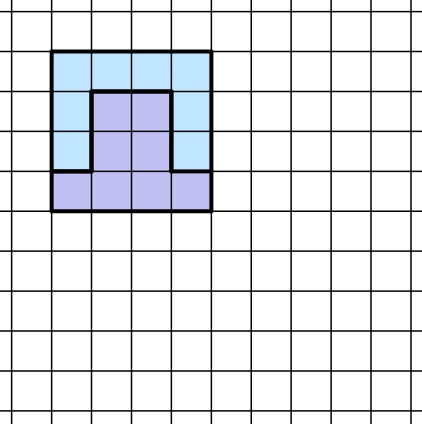
II. Bei weiterer Betrachtung aller Formen ist auffällig, das sich aus der Zusammensetzung der fünften Figur und der fünften Form um 180° gedreht ein 4∙4 Kästchen großes Quadrat ergibt:

 

 

Ein 8∙8 Kästchen großes Quadrat lässt sich jetzt durch Zusammensetzen von vier solcher 4∙4 Kästchen großen Quadrate parkettieren:

 

 

 

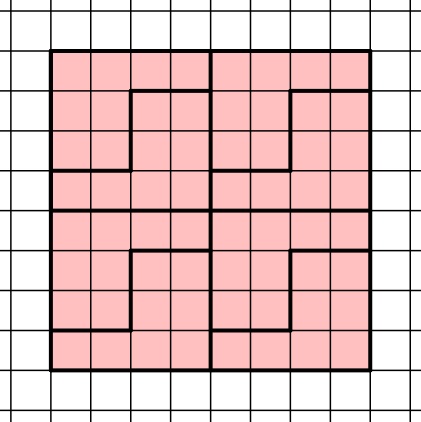
Somit sind zwei Möglichkeiten, das 8∙8 Kästchen große Quadrat mit einer einzigen Form zu parkettieren, angegeben.

 

 

Aufgabenteil b)

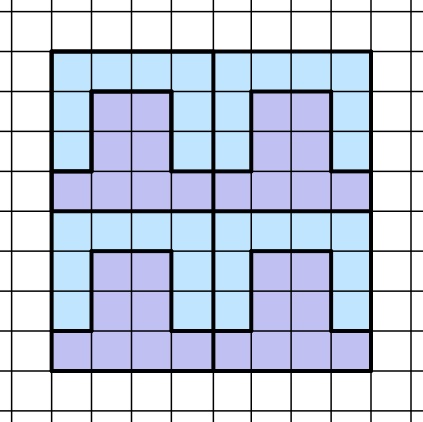
I. Blickt man auf Aufgabenteil a zurück, so lässt sich leicht erkennen, dass sich ein 8∙8 Kästchen großes Quadrat mit der zweiten und der fünften Form parkettieren lässt:

 

 

 

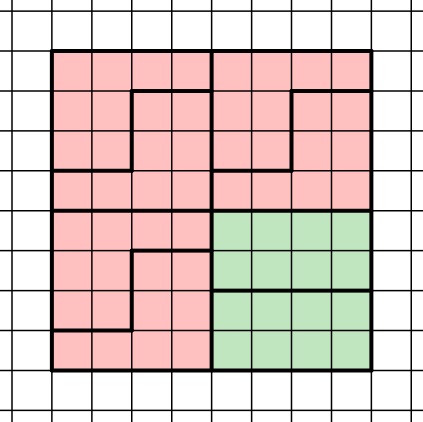
II. Sowohl zwei der zweiten Form als auch zwei der vierten Form lassen sich jeweils zu einem 2∙8 Kästchen großen Rechteck zusammensetzen.

 

                 

 

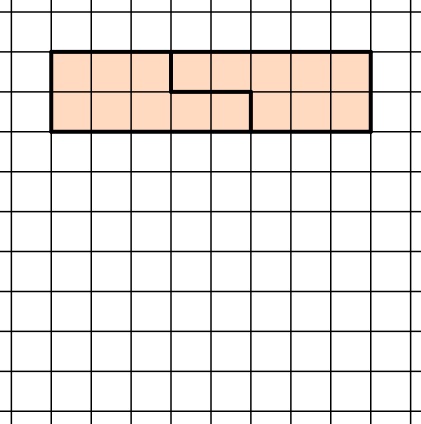
Vier dieser Rechtecke ergeben zusammengesetzt ein 8∙8 Kästchen großes Quadrat, denn 8:8=1, 8:2=4 und 1∙4=4. Bei der Zusammensetzung muss darauf geachtet werden, dass beide Rechtecke jeweils mindestens einmal auftreten. Es ergibt sich beispielsweise folgende Parkettierung:

 

 

 
III. Bei Rückblick auf die zweite Möglichkeit in Aufgabenteil a) und auf die zweite Möglichkeit in diesem Teil wird deutlich, dass eine Parkettierung durch die vierte und die fünfte Form ebenfalls möglich ist:
 

 

 
 
IV. Bei Betrachtung der Ausgangsformen lässt sich erkennen, dass sich durch die erste und die dritte Form ein 4∙4 Kästchen großes Quadrat zusammensetzen lässt:
 

 

Somit lässt sich aus diesen Formen auch ein 8∙8 Kästchen großes Quadrat auslegen:
 
 

 

 
 
 
Aufgabenteil c)
 

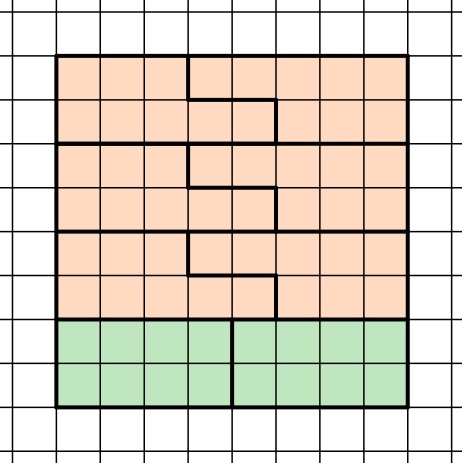
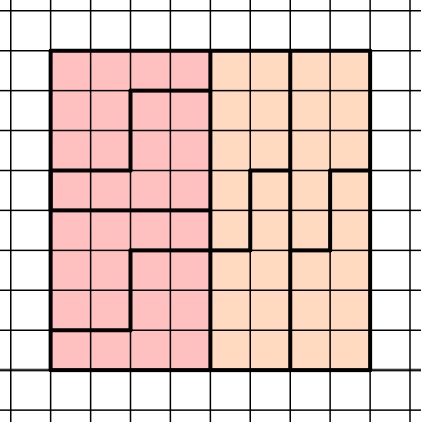
I. Durch Zusammensetzen des 4∙4 Kästchen großen Quadrats aus a)II. und des 4∙4 Kästchen große Quadrats aus b)IV. ergibt sich bereits ein 4∙8 Kästchen großes Rechteck aus drei unterschiedlichen Formen, nämlich der ersten, der dritten und der fünften Form:

 

 

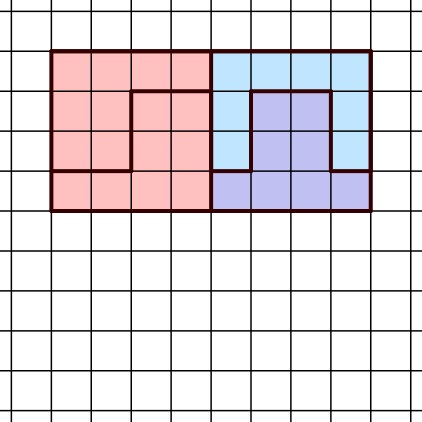
Dieses Rechteck lässt sich nun mit der zweiten Form zu einem 8∙8 Kästchen großen Quadrat ergänzen:

 

 
 
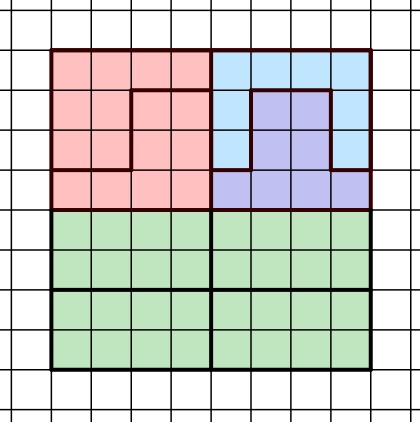
II. Das obige 4∙8 Kästchen große Rechteck lässt sich auch durch die vierte Form zu einem 8∙8 Kästchen großes Quadrat ergänzen. Die einzelnen Bestandteile aus den vorherigen Aufgabenteilen können dabei aus ästhetischen Gründen auch rotiert und verschoben werden, sodass das Parkett dem jeweiligen Geschmack entsprechend verlegt werden kann.

 

 
 
Diese beiden Möglichkeiten stimmen nicht in allen vier Formen überein und somit ist auch der Aufgabenteil c gelöst worden.
 

Die Aufgabe wurde für die sechste Klassenstufe entwickelt. Allerdings nehmen an der Mathematik-Olympiade größtenteils sehr leistungsstarke Schülerinnen und Schüler teil, weswegen sie in differenzierter Ausführung in die Klasse gegeben werden sollte (siehe Differenzierungsmöglichkeiten). Die geförderten inhaltlichen Kompetenzen (siehe Geförderte Kompetenzen) beziehen sich im Rahmenlehrplan auf die Niveaustufen C und D, wodurch die Formen-Puzzle-Aufgabe für den Einsatz in der sechsten Jahrgangsstufe in der Thematik Kongruenzabbildungen (Rotationen, Translationen, Achsenspiegelungen, Punktspiegelungen, etc.) geeignet ist.

 

 


In Hinblick auf den brandenburgischen Rahmenlehrplan Mathematik für die Jahrgangsstufen 1-10, der ab dem Schuljahr 2017/18 gültig ist (vgl. LISUM 2015), kann die Aufgabe unter folgenden Aspekten eingeordnet werden: Bei den Prozessbezogenen Kompetenzen werden primär die Bereiche [K4] Mathematische Darstellungen verwenden und [K2] Probleme mathematisch lösen angesprochen, während bezüglich der Inhaltsbezogenen Kompetenzen der Teilbereich [L3] Raum und Form im Mittelpunkt steht. Die Aufgabe entspricht dem Anforderungsbereich III, da die Kinder, die für die Aufgabe notwendigen Fähigkeiten und Kenntnisse erkennen müssen, um sie zu lösen. Dies entspricht einem Transfer des erworbenen Wissens auf eine neue Problemstellung.

 

 

Prozessbezogene Kompetenzformulierungen
 

Mathematische Darstellungen [K4]
Kompetenz 1: Die Schülerinnen und Schüler können die vorgegebenen Formen analysieren und setzen sie in Beziehung, um ein Quadrat mit 8∙8 Kästchen restlos auszufüllen.

"Mathematisches Arbeiten zeichnet sich durch Auswählen, Anfertigen und Interpretieren solcher [enaktiver, verbaler, numerischer, grafischer oder mathematisch-symbolischer] Darstellungen aus" (LISUM 2015, S. 7)

Begründung: Die Schülerinnen und Schüler erkennen, wie viele Kästchen jede Form besitzt. Sie wissen durch Multiplikation wie viele Kästchen ein 8∙8 Kästchen großes Quadrat besitzt. Daher können sie die Teilfiguren so zusammenfügen, das sie 8 Kästchen in der Länge nicht überschreiten, zusammengesetzt das vorgegebene Quadrat bilden und/oder kleinere Quadrate mit 4∙4 Kästchen zusammensetzen, die sich zum vorgegebenen Quadrat ergänzen lassen.

 

Probleme mathematisch lösen [K2]
Kompetenz 2: Die Schülerinnen und Schüler können das heuristische Ergänzungs-/Zerlegungsprinzip anwenden, indem sie die vorgegebenen Teilfiguren durch weitere Formen zu Quadraten mit 8∙8 Kästchen ergänzen bzw. Quadrate mit 8∙8 Kästchen in die vorgegebenen Teilfiguren zerlegen.

"Die Schülerinnen und Schüler können heuristische Hilfsmittel zum Problemlösen anwenden" (LISUM 2015, S.19)

Begründung: Die Aufgabe stellt verschiedene Teilfiguren zur Verfügung, aus denen diejenigen herausgesucht werden müssen, die sich nach Vorgabe zu einer Gesamtfigur ergänzen bzw. in die sich die vorgegebene Gesamtfigur zerlegen lässt. Das bedeutet, dass hier einige Teilfiguren vorliegen, mit denen die Lösung möglich ist. Die Kinder müssen auf Basis ihrer räumlichen Fähigkeiten geeignete Formen auswählen.

 

Kompetenz 3: Die Schülerinnen und Schüler können verschiedene Lösungsmöglichkeiten entwickeln.

"Die Schülerinnen und Schüler können Zusammenhänge erkennen und Lösungsstrategien auf ähnliche Sachverhalte übertragen." (LISUM 2015, S.19)

Begründung: Die Schülerinnen und Schüler müssen sich in Teilaufgabe a) überlegen, wie sie zu einer Lösung gelangen (beispielsweise durch das Zerlegungs-/Ergänzungsprinzip). Bei dieser Lösung soll das 8∙8 Kästchen große Quadrat mit einer einzigen Form parkettiert werden. Bei Teilaufgabe b) sollen zwei Formen genutzt werden und bei Teilaufgabe c) sogar vier Formen. Trotz der Zunahme der Nebenbedingungen und somit des steigenden Schwierigkeitsgrades können die Lernenden einen Zusammenhang zu Aufgabenteil a) erkennen und diese Aufgaben nach dem gleichen Prinzip lösen.

 

 

Inhaltsbezogene Kompetenzformulierungen

 

Raum und Form [L3]
Kompetenz 4: Die Schülerinnen und Schüler können vorgegebene Teilfiguren zu einem Quadrat mit 8∙8 Kästchen restlos ergänzen.

"Herstellen von Parketten durch Zeichnen und Legen von Figuren" (LISUM 2015, Geometrische Abbildungen ausführen, Niveaustufe D, S.49)

Begründung: Der Schwerpunkt der zu lösenden Aufgabe liegt darauf, die räumliche Fähigkeit der Figur-Grund-Unterscheidung (visuelle Wahrnehmung) anzuwenden (vgl. Franke, 2016, S.89). Die Lernenden müssen wissen, dass sich eine Gesamtfigur in Teilfiguren zerlegen lässt bzw. dass sich Teilfiguren zu einer Gesamtfigur ergänzen lassen, und sie müssen dies anwenden können.

 

Kompetenz 5: Die Schülerinnen und Schüler können die vorgegebenen Teilfiguren im Kopf veranschaulichen (Räumliches Vorstellungsvermögen nach Franke, 2016, S.67ff).

"Erkennen und Benennen gespiegelter, verschobener und gedrehter ebener Figuren" (LISUM 2015, Geometrische Abbildung und ihre Eigenschaften nutzen, Niveaustufe C, S.47), "Beschreiben von Lagebeziehungen" (LISUM 2015, Beziehung zwischen geometrische Objekten beschreiben, Niveaustufe D, S.48)

Begründung: Damit die Schülerinnen und Schüler gedanklich Teilfiguren bilden können, ist es notwendig sie gedanklich zu verändern (vgl. Franke, 2016, S.67). Diese räumliche Fähigkeit, mit den Objekten zu operieren, ist die Voraussetzung, um die Teilfiguren zu ermitteln, die zu den verschiedenen Lösungen führen.

 

Kompetenz 6: Die Schülerinnen und Schüler können Achsen-, Punkt- und Drehsymmetrie erkennen und für ihren Lösungsweg einsetzen.

"Zeichnen von Spiegelbildern auf Rasterpapier" (LISUM 2015, Geometrische Abbildung ausführen, Niveaustufe C, S.47)

Begründung durch einige Beispiele:

  • Um eine kongruente Figur (bis auf das Rechteck) zu erhalten, muss eine Dreh- bzw. Punktsymmetrie vorliegen.
  • Wenn die Lernenden eine Teilfigur verdoppelt haben, kann beispielsweise ein 4∙4 Quadrat entstanden sein.
    Wenn sie diese zum vorgegebenen Quadrat zusammensetzen, erhalten sie eine symmetrische Figur (Achsen-, Punktsymmetrie).
  • Haben die Schülerinnen und Schüler Aufgabe a) gelöst, könnten sie z.B. zwei 4∙4 Quadrate verschiedener Lösungen, die jeweils aus einer Teilfigur gebildet wurden, zu einem neuen vorgegebenen Quadrat zusammensetzen und hätten eine Lösung für b).

 

 

Literatur:

Franke, M., & Reinhold, S. (2016). Mathematik Primarstufe und Sekundarstufe I + II: Didaktik der Geometrie in der Grundschule (3. Auflage). Berlin: Springer Spektrum.


Heuristische Hilfsmittel: 
  • In beiden Lösungen werden Zeichnungen erstellt. Insbesondere beim zweiten Lösungsweg wird immer wieder auf vorherige Zeichnungen (Parkettierungen) zurückgegriffen und diese werden zum Teil abgewandelt. Somit stellen die Zeichnungen Informative Figuren dar.

 

 

Heuristische Strategien: 

Die beiden dargestellten Lösungswege unterscheiden sich grundsätzlich durch die unterschiedlichen angewandten Heuristischen Strategien.

 

Beim ersten Lösungsweg werden folgende Strategien genutzt:

  • Vorwärtsarbeiten: Die einzelnen Formen werden der Reihe nach durchgegangen und es wird ausprobiert, ob eine Parkettierung eines 8∙8 Kästchen großen Quadrats mit den jeweiligen Formen möglich ist. Es wird also vom Gegebenen ausgegangen und unter Berücksichtigung der durch die Aufgabenstellung gegebenen Bedingungen nach Lösungen gesucht.

 

  • Systematisches Probieren: Die einzelnen Formen und Kombinationen der Formen werden systematisch durchgegangen.

 

Der zweite Lösungsweg nutzt diese Strategien:

  • Kombiniertes Vorwärts- und Rückwärtsarbeiten: Es wird zunächst das Gesuchte betrachtet und in diesem Zusammenhang das 8∙8 Kästchen große Quadrat. Daraufhin folgt die Überlegung, welche Bedingungen die Seitenlängen der Formen (also das Gegebene) erfüllen müssen, damit das Quadrat mit diesen ausgelegt werden kann (Rückwärtsarbeiten). Außgehend vom Gegebenen werden dann unter Berücksichtigung der in der Aufgabenstellung festgelegten Bedingungen Lösungen gefunden (Vorwärtsarbeiten).

 

  • Analogieschlüsse: In allen Teilaufgaben wird auf die gleiche Art und Weise vorgegangen. Es wird nach Teilvierecken gesucht, deren Seitenlängen jeweils ein Teiler der Seitenlänge des zu parkettierenden Quadrats sind (bzw. eine gerade Zahl), sodass sich dieses aus den gefundenen Rechtecken, welche wiederum aus vorgegebenen Figuren bestehen, zusammensetzen lässt. Darüber hinaus werden bereits gefundene Rechtecke bei darauffolgenden Lösungen immer wieder verwendet.

 

 

Heuristische Prinzipien: 
  • Beim ersten Lösungsweg wird das Quadrat durch die gegebenen Formen zusammengesetzt, hier spielt also das Ergänzungsprinzip eine Rolle. Beim zweiten Lösungsweg ist sowohl das Ergänzungs- als auch das Zerlegungsprinzip von Bedeutung. So werden hier bereits gefundene Lösungen wieder in einzelne Bestandteile zerlegt, aus denen wiederum das 8∙8 Kästchen große Quadrat neu zusammengesetzt wird.

 

  • Bei beiden Lösungsvarianten wird das Invarianzprinzip verwendet. So verändert sich die zu parkettierende Fläche, nämlich das 8∙8 Kästchen große Quadrat, nicht. Auch die einzelnen gegebenen Formen müssen deckungsgleich bleiben, sie dürfen nur in ihrer Lage verändert werden.

 

  • Auch das Symmetrieprinzip ist von Bedeutung: Bei der Lösung des Aufgabenteils c) beim zweiten Lösungsweg wird die zweite Lösungsmöglichkeit gefunden, indem einfach das 2∙8 Kästchen große Rechteck, welches aus zwei der zweiten Form besteht, durch das 2∙8 Kästchen große Rechteck, welches aus zwei der vierten Form besteht, ausgetauscht wird. Hier wird also beispielsweise die gleiche Fläche der Rechtecke, welche aber aus unterschiedlichen Formen zusammengesetzt sind, genutzt.

Die Aufgabe "Formen-Puzzle" hat nach Cohors-Fresenborg et al. sowohl bezüglich des ersten dargestellten Lösungsweges mit 3 erreichten Punkten als auch bezüglich des zweiten Lösungsweges mit 4 erreichten Punkten einen Schwierigkeitsgrad von **.

 

 

Sprachlogische Komplexität: 

Die Aufgabenstellung ist in mehreren Haupt- und Nebensätzen formuliert. Die zusätzliche Informationen "sie müssen nicht in der gleichen Anzahl vorkommen" in Aufgabenteil b) und c), die mehr Freiraum für die Lösung lässt, ist durch ein Semikolon abgetrennt und somit übersichtlich dargestellt. Die Reihenfolge der Satzteile entspricht jeweils nicht den Schritten der mathematischen Bearbeitung und es sind auch für die Lösung unrelevante Informationen, wie "In einem Puzzle gibt es acht verschiedene, rechtwinklige, flächengleiche Formen, die jeweils acht Kästchen umfassen." enthalten. Somit lässt sich die Sprachlogische Komplexität der Aufgabe auf Stufe 1 einordnen. 

 

 

Kognitive Komplexität: 

Bei der Lösung von Aufgabenteil b) und c) sind Zusatzüberlegungen wie "Möglichkeiten, die sich untereinander jeweils in mindestens einer der verwendeten Formen unterscheiden" und "Möglichkeiten, die nicht in allen vier verwendeten Formen übereinstimmen" zu berücksichtigen. Darüber hinaus müssen bei beiden Lösungen vorher Überlegungen gemacht werden, wie vorgegangen wird bzw. welche Heurismen verwendet werden (vergleiche "Grundgedanke" bei den Lösungen). Somit hat die Aufgabe eine Kognitive Komplexität der Stufe 2.

 

 

Formalisierung von Wissen: 

Weder beim ersten noch beim zweiten Lösungsweg sind die Lösungen lediglich in zeichnerischer Form zu erstellen. Daher lässt sich die Aufgabe bezüglich der Formalisierung von Wissen auf Stufe 0 ansiedeln.

 

 

Formelhandhabung: 

Bei der ersten Lösung sind keine algebraischen Operationen erforderlich. Wird die Aufgabe auf diese Weise gelöst, so lässt sich die Formelhandhabung auf Stufe 0 einordnen. Bezüglich des zweiten Lösungsweges lässt sich die Formelhandhabung aber auf Stufe 1 ansiedeln. Bei dieser Lösung sind zwar auch keine Gleichungen oder Terme aufzuschreiben, es muss aber im Kopf die Zerlegung der Zahl 8 in Teiler erfolgen sowie Rechenoperationen beim Zusammensetzen verschiedener Rechtecke zu dem gesuchten Quadrat angewandt werden.

 

 

Stufenzuordnung: 
Formalisierung von Wissen
Stufe 0
Formelhandhabung
Stufe 0
Stufe 1
Kognitive Komplexität
Stufe 2
Sprachlogische Komplexität
Stufe 1

Hilfestellungen: 

Beim Bearbeiten der "Formen-Puzzle" - Aufgabe können vor allem Probleme dabei auftreten, eine sinnvolle Herangehensweise an die Aufgabe zu entwickeln. So kann es sein, dass die Schülerinnen und Schüler nicht auf die Idee kommen, aus den gegebenen Formen Rechtecke zusammenzusetzen, aus denen sie wiederum das zu parkettierende Quadrat auf unterschiedliche Weise "zusammenpuzzeln" können. In diesem Fall können folgende Hilfen gegeben werden:

Allgemein-strategische Hilfen Inhaltsorientierte strategische Hilfen Inhaltliche Hilfen
Was ist gegeben? Hilft es dir, das 8∙8 Kästchen große Quadrat in sinnvolle kleinere Teile zu zerlegen? Lassen sich Formen zu kleineren Rechtecken oder Quadraten zusammensetzen?
Untersuche die Formen genau! Vergleiche die Eigenschaften der Formen mit denen des zu parkettierenden Quadrats! Welche Eigenschaften der Formen sind bei der Parkettierung von Bedeutung?
Was fällt dir an den Formen auf?

Kannst du nützlichere kleinere Figuren mit den gegebenen Formen zusammensetzen?

Geben dir die Seitenlängen der einzelnen Formen Hinweise darauf, ob sich diese zum 8∙8 Kästchen großen Quadrat zusammensetzen lassen?

 

Außerdem kann es für die Lernenden problematisch sein bei der Bearbeitung von Aufgabenteil b) und c) auf den Gedanken zu kommen, bereits gefundene Lösungen wieder zu zerlegen und aus diesen Zerlegungen ein neues Quadrat zusammenzusetzen. Tritt diese Schwierigkeit auf, so können beispielsweise die im Folgenden dargestellten Hilfen gegeben werden.

Allgemein-strategische Hilfen Inhaltsorientierte strategische Hilfen Inhaltliche Hilfen

Arbeite mit deinen vorherigen Lösungen weiter!

 

 Kannst du vorherige Lösungsmöglichkeiten sinnvoll zerlegen? Welche Eigenschaften müssen Rechtecke haben, die sich zu dem gesuchten Quadrat zusammensetzen lassen? Kannst du solche Rechtecke in deinen bisherigen Lösungen finden?
Betrachte deine Lösungsmöglichkeiten aus den vorherigen Aufgabenteilen! - -
Welche Bedingungen müssen laut Aufgabenstellung erfüllt sein? Was ist dir freigestellt? Du darfst auch Formen verwenden, die du in vorherigen Aufgabenteilen verwendet hast! Kannst du Teile einer oder mehrerer vorheriger Lösungsmöglichkeiten wiederverwenden?

 

 

Sozialformen: 
  • Einzelarbeit
  • Gruppenarbeit ("Mathe-Konferenz")

 

 

Differenzierungsmöglichkeiten: 

Die Aufgabe weist, so wie sie gestellt ist, schon einen gewissen Differenzierungsgrad auf: Zum einen durch die gegebenen Formen, die mehr oder weniger komplex sind (vergleicht man Form 2 mit 6). Zum anderen unterscheiden sich auch die einzelnen Teilaufgaben in ihrer Komplexität. Bei Aufgabenteil a) muss sich nur für eine Form entschieden werden, bei b) dann für zwei, die zusammen das Quadrat füllen und bei c) sollen sogar vier verschiedene Flächen genutzt werden. Es müssen also von Teilaufgabe zu Teilaufgabe immer mehr Bedingungen berücksichtigt werden.

 

Die Aufgabenstellung kann aber noch weiter differenziert werden. Für leistungsschwächere Kinder könnten einige Formen gestrichen werden und die Aufgabe kann auf die Teilaufgabe a) und b) beschränkt werden. Werden die Formen 1 bis 5 ausgewählt, können immer noch alle Möglichkeiten für a) und b) gefunden werden. Durch die kleinere Auswahl wird die Aufgabe überschaubarer. Es könnte auch noch eine Übung vor a) gesetzt werden, in der ein 4∙4 Kästchen großes Quadrat gefüllt werden muss. So können auf kleinerem Raum schon viele Möglichkeiten erkundet werden, die dann auf das große Kästchen übertragen werden können. Des Weiteren kann den Schülerinnen und Schülern angeboten werden, die Formen auszuschneiden und sie zu legen, falls diese noch Schwierigkeiten mit der Rotation im Kopf haben.

 

Für die leistungsstarken Schülerinnen und Schüler kann noch eine zusätzliche Aufgabe angeboten werden, in der überprüft werden soll, ob das Kästchen mit allen acht Formen gefüllt werden kann.


Diese Aufgabe eignet sich für das Forschen. Sobald Kinder mit dem Thema des Zerlegens und Ergänzens vertraut sind, kann diese Aufgaben als Forschungsaufgabe gestellt werden. Da sie eine innere Differenzierung enthält, die sich erweitern lässt (siehe Differenzierungsmöglichkeiten), können alle Lernenden einer Klasse die Aufgaben auf verschiedenen Niveaustufen bearbeiten. Nach der Bearbeitungsphase kommen die Kinder in Konferenzen zusammen, um ihre Ergebnisse zu vergleichen. Durch diese Zusammenkünfte erhalten sie Einblicke in unterschiedliche Herangehensweisen und Lösungen für die Aufgabe. Als Abschluss werden in einer gemeinsamen Runde die Ergebnisse unter den Aspekten "So rechnen wir" und "Diese Rechenwege sind besonders schlau" mit den Kindern zusammengefasst und fixiert (in Anlehnung an die Methode "Mathe-Konferenz" von Pikas (https://pikas.dzlm.de/pikas-kompakt/mit-pikas-unterrichten/infoheft-um, S.11 (letzter Zugriff: 02. August 2017)). Dadurch erhalten die Kinder ein differenziertes Bild über verschiedene Lösungsansätze und -wege, die ihnen bei späteren Aufgaben helfen.



Bearbeitet von: Henrike Bohne, Linda Scheunemann (ergänzt von Marisa Pfläging)
nach oben
430 Nutzer/-innen haben abgestimmt.

Feedback

Wir freuen uns auf Ihre Anregungen und konstruktive Rückmeldung zum Material.