Garten-Deal

Fehlermeldung

Deprecated function: The each() function is deprecated. This message will be suppressed on further calls in FieldCollectionItemEntity->fetchHostDetails() (Zeile 313 von /www/htdocs/w0127817/beta.proffi-m.de/sites/all/modules/field_collection/field_collection.entity.inc).
Klasse Schulstufe Thema Themengebiet Schwierigkeit
5 Primarstufe Flächeninhalte von Rechtecken Größen und Messen, Raum und Form, Zahlen und Operationen *

Aufgabenstellung

Mareike und Julian dürfen ein rechteckiges Beet im Garten ihrer Eltern selber bepflanzen. Julian schlägt Mareike vor:
„Lass uns einfach jeweils die Breite und Länge des Rechtecks um die Hälfte verkürzen. Dann hast du deinen Teil und
ich nehme den Rest.“
Soll sich Mareike auf diesen Deal einlassen? Erkläre.
 

Quellenangabe:

Gebel, I. & Kuzle, A. (2016). MatheWelt. Problemlösetraining in der Geometrie. Velber: Friedrich Verlag GmbH. S.6.


ein reschteckiges Blumenbeet, bei dem die Breite und Länge um die Hälfte verkürzt werden soll; dieser Teil soll dann Mareike gehören, während Julian den Rest nimmt.
gegeben:
 
 
 
 
gesucht: 
Julians Fläche, Mareikes Fläche
 
 
 
 
 
Lösungsvariante 1 - Zeichnerische Lösung
 
Zunächst wird zur visuellen Verdeutlichung ein beliebiges Rechteck aufgezeichnet, an dem sowohl die Längenseite als auch die Breitenseite durch einen Strich in zwei gleich große Hälften geteilt wird.
 
 
Die beiden Striche werden dann jeweils verlängert, bis sie aufeinander treffen. Das dadurch entstandene Rechteck ist Mareikes Teil des Beets. Der Rest würde nach dem Deal Julian gehören.
 
 
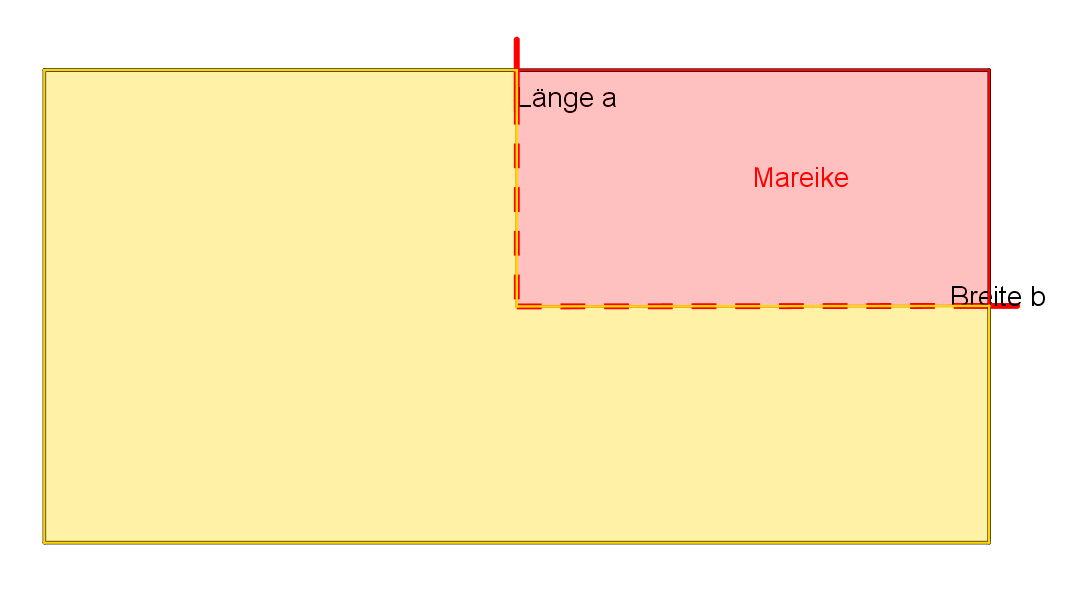
Um nun aber auch noch herauszufinden wie groß die jeweiligen Teile sind, wird das komplette Rechteck einmal waagerecht in zwei gleichgroße Teile geteilt, indem eine Mittelsenkrechte an einer der Breitenseiten konstruiert wird. Gleiches wird bei den Längenseiten gemacht. Wir erkennen, dass das Rechteck so in 4 gleich große kleinere Rechtecke geteilt werden kann und Julian drei davon bepflanzen kann, Mareike allerdings nur eins, nämlich das rot markierte. Demnach ist Julians Teil \(\frac { 3 }{ 4 } \) von der eigentlichen Rechteckfläche groß, und Mareikes nur \(\frac { 1}{ 4 } \).
 
 
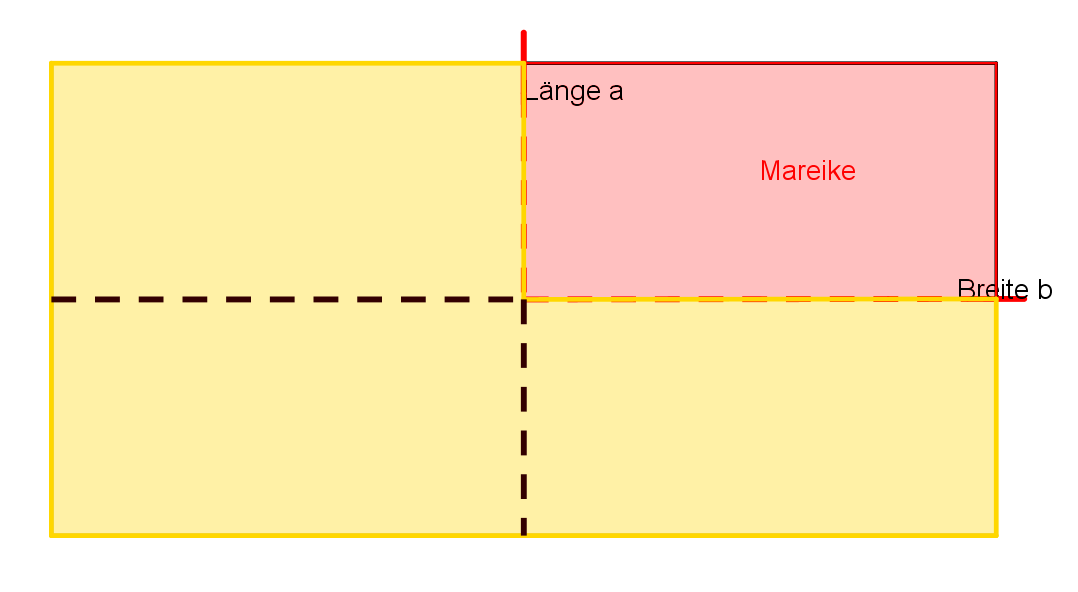
Somit sollte sich Mareike nicht auf den Deal einlassen, da sie mit diesem nur noch \(\frac { 1 }{ 4 } \) der Fläche zum Bepflanzen hat
und ihre Fläche dreimal so klein wäre wie die ihres Bruders.
 
 
 
Lösungsvariante 2 - Allgemeine rechnerische Lösung
 
Dieser Art von Lösung liegt die Rechteckflächenformel \(A=a\cdot b\) zugrunde. Anhand dieser Formel wird der Deal verdeutlicht, in welchem es ja darum ging, dass die Länge (a) und die Breite (b) um die Hälfte verkürzt werden. Diese gegebene Information wird in die eigentliche Rechteckflächenformel aufgenommen und daraus wird die Formel abgeleitet, mit der die Größe der Fläche bestimmt werden kann, die Mareike nach dem Deal bepflanzen dürfte:
 
  \({ A }_{ Rechteck,\quad gesamt }=a\cdot b\)
\(\Rightarrow \) \({ A }_{ Mareike,\quad Teil }=\frac { 1 }{ 2 } \cdot a\cdot \frac { 1 }{ 2 } \cdot b\)
\(\Leftrightarrow \) \({ A }_{ Mareike,\quad Teil }=\frac { 1 }{ 4 } \cdot a\cdot b\)
 
Hieraus ergibt sich, dass Mareike nur noch ein Viertel der eigentlichen Rechteckfläche bepflanzen könnte.
 
Dies lässt sich auch noch durch eine Probe der Formel anhand von Beispielwerten beweisen. Als Beispiel habe ich für die Länge \( 6 cm\) gewählt und für die Breite \(4 cm\). Dadurch ergibt sich für das gesamte Beet eine Fläche von \(24 cm²\) und durch einsetzen in die oben ermittelte Flächeninhaltsformel für Mareikes Teil eine Fläche von \(6 cm²\). Auch ohne die Berechnung von Mareikes Teil durch die Formel, würde \(6 cm²\) als Fläche resultieren, denn mit \(\frac { a }{ 2 } =3 cm\) und \(\frac { b }{ 2 } =2 cm\) ergibt sich \({ A }_{ Mareike}=3cm \cdot 2cm=6cm²\). Somit ist die Formel korrekt.
 
Durch diese Erkenntnis, kann nun auch sowohl anhand der Formel, als auch anhand der Beispielrechnung gesagt werden, dass für Mareike mit dem Deal nur noch \(\frac { 1 }{ 4 } \) der eigentlichen Beetfläche übrig bleiben würde, da \(6cm²\) der vierte Teil von \(24cm²\) ist, denn \(\frac { 24cm² }{ 6cm² } =4\). Ihr Bruder Julian hingegen könnte eine Fläche von \(18 cm² \) bepflanzen, was dreimal so viel wäre wie Mareikes Teil, denn \(6cm²\cdot 3=18cm²\). Aus diesem Grund würde ich Mareike von dem Deal abraten, da sie eine viel geringe Fläche bepflanzen könnte als ihr Bruder.
 
 
 
Lösungsvariante 3 - Zeichnerische Lösung mit Abmessungen
 
Zunächst zeichne ich ein beliebiges Rechteck.
 
 
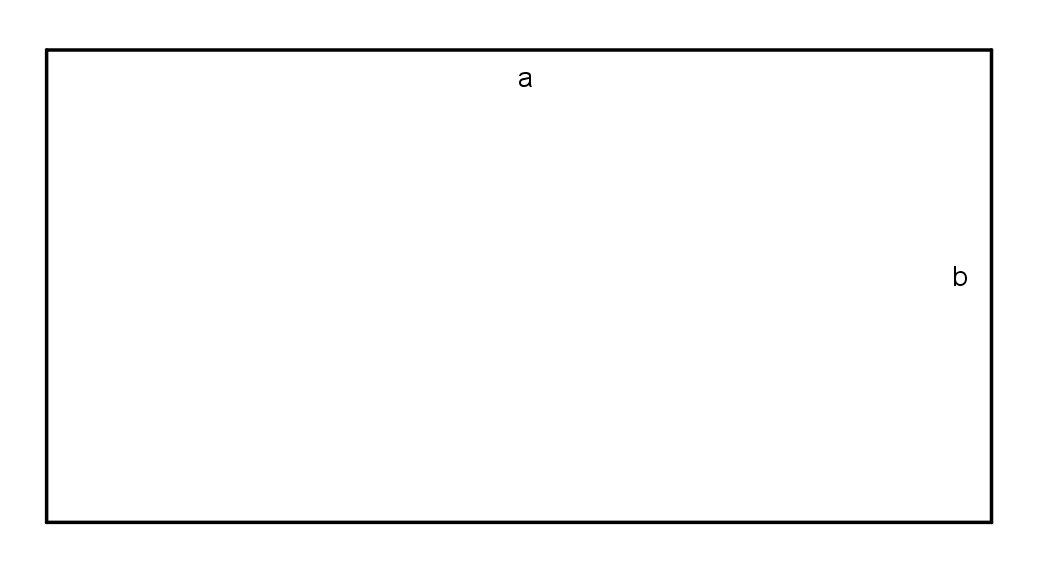
Durch Abmessungen mit dem Geodreieck, weiß ich, dass die Länge des Rechtecks \(a = 6 cm\) und die Breite \(b = 4 cm\) beträgt.
Um die Hälfte der Länge a und Breite b zu errechnen dividiere ich jeweils durch zwei:
\(\frac { a }{ 2 } =\frac { 6cm }{ 2 } =3cm\)
\(\frac { b }{ 2 } =\frac { 4cm }{ 2 } =2cm\)
 
Mit dem Geodreieck markiere ich die Hälfte von a und zeichne im rechten Winkel eine Strecke der Länge \(\frac { b }{ 2 } = 2 cm \) ein. An demjenigen Endpunkt dieser Strecke, welcher nicht auf der Seite a liegt, zeichne ich mit dem Geodreieck im rechten Winkel eine Länge der Strecke \(\frac { a }{ 2 } = 3cm\).
 
 
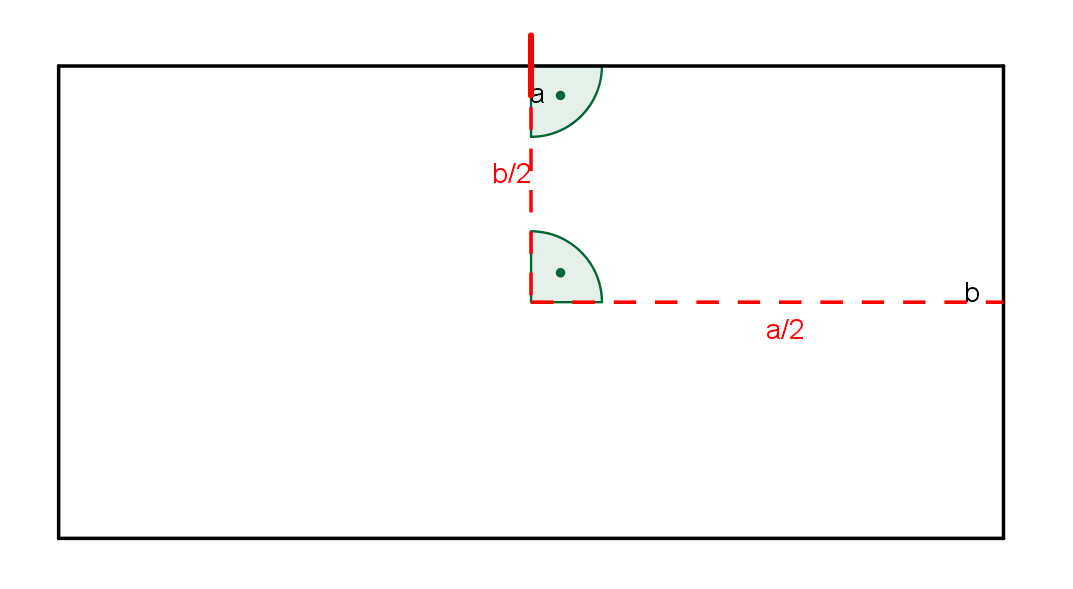
Aus der Zeichnung geht hervor, dass der Umpfang von Mareikes Beet nur ein Viertel des Gesamtumpfangs beträgt.
 
 
 
Lösungsvariante 4 - Rechnerische Lösung mit selbst gewählten Zahlen
 
Zunächst wird die Flächeninhaltsformel für ein Rechteck angewandt:
 
\(A=a \dot\ b\)
 
Wähle für das Beet ein Rechteck der Länge \(a = 6cm\) und der Breite \(b=4cm\).
Mit den Abmessungen folgt für den Flächeninhalt des gesamten Beets:
 
\(A=6cm \dot\ 4cm=24cm²\)
 
Julian schlägt Mareike vor ein Beet mit der Hälfte der Seitenlängen des Ursprungsbeets zu bepflanzen. Für die Fläche von Mareikes Teil würde dann gelten:
\(A_M=\frac { a }{ 2 } \dot\ \frac { b }{ 2 } =3cm \dot\ 2cm=6cm²\)
 
Der Flächeninhalt von Mareikes Teil würde mit dem Deal 6 cm² betragen, was ein Viertel der Fläche des Ursprungsbeetes wäre. Somit sollte man Mareike von dem Deal abraten.

Die Garten-Deal-Aufgabe wurde für eine fünfte Klasse konzipiert. Die Schülerinnen und Schüler müssen hierbei über Kompetenzen auf Niveaustufe C verfügen. Ein Beispiel hierfür ist das Berechnen des Flächeninhalts, welches zum inhaltsbezogen Kompetenzbereich „Größen und Messen“ gehört. Hier wird in der Niveaustufe C formuliert: „Die Schülerinnen und Schüler können Größen messen (auch Massen und Flächeninhalte).“ Im Kompetenzbereich „Raum und Form“ wird im Unterpunkt „geometrische Objekte“ in Niveaustufe C beschrieben, dass die Kinder ebene, geometrische Figuren zeichnen können. Dies stellt eine weitere Kompetenz dar, welche eine Voraussetzung für das Lösen der Aufgabe ist. Notwendiges Vorwissen für diese Aufgabe sind erweitertes Wissen über die Fläche eines Rechtecks und Kenntnisse über die Bruchrechnung oder andere vereinfachte Darstellungsformen der Multiplikation. Über diese Kenntnisse sollten Schülerinnen und Schüler der fünften Klasse verfügen.
 
Für besonders fitte Kinder kann die Aufgabe sicherlich auch vor der fünften Klasse eingesetzt werden, da sie zum Teil ein Gedankenexperiment ist und mit einer einfachen, logischen Überlegung lösbar ist. 

Mit der Garten-Deal-Aufgabe werden sowohl inhaltliche als auch prozessbezogene Kompetenzen gefördert. Diese werden im Folgenden genannt und erläutert sowie mit dem brandenburgischen Rahmenlehrplan "Teil C. Mathematik. Jahrgangsstufen 1-10. 2015", der ab dem Schuljahr 2017/18 gültig ist (im Folgenden als RLP bezeichnet), in Bezug gesetzt.
 
 
Inhaltsbezogene Kompetenzformulierungen
 
Zahlen und Operationen:
  • Die Schülerinnen und Schüler können die Rechenverfahren der Grundrechenoperationen anwenden.
"Die Schülerinnen und Schüler können die Rechenstrategien und Gesetze der Grundrechenoperationen im Bereich der natürlichen Zahlen bis 100 situationsangemessen nutzen" (RLP, Rechenverfahren und -strategien anwenden, Niveaustufe B, S.23)
Die Schülerinnen und Schüler können in dieser Aufgabe dividieren und multiplizieren.
 
 
Größen und Messen:
  • Die Schülerinnen und Schüler kennen die Maßeinheit Meter und können mit dieser rechnen.
"Die Schülerinnen und Schüler können die verschiedenen Größen und ihre Einheiten nutzen" (RLP, Vorstellungen zu Größen und ihren Einheiten nutzen, Niveaustufe C, S.24)
Beim rechnerischen Lösungsweg mit selbst gewähltem Zahlenbeispiel sowie beim allgemeinen rechnerischen Lösungsweg (bei der Proberechnung) legen die Schülerinnen und Schüler die Maße des Beetes fest und rechnen mit diesen.
 

Raum und Form:
  • Die Schülerinnen und Schüler können ein Rechteck zeichnen und an diesem arbeiten.
 "Die Schülerinnen und Schüler können ausgewählte geometrische Objekte herstellen und zeichnen" (RLP, Geometrische Objekte darstellen, Niveaustufe B, S.26)
Beim zeichnerischen Lösungsweg wird eine Skizze vom Beet angefertigt und die Aufgabe damit gelöst.
 
 
 
 
Prozessbezogene Kompetenzformulierungen
 
Mathematisch argumentieren:
  • Die Schülerinnen und Schüler können Begründungen selbstständig entwickeln.
"Die Schülerinnen und Schüler können Begründungen [...] zunehmend selbstständig entwickeln" (RLP, S.19)
In dieser Aufgabe müssen die Schülerinnen und Schüler ein Problem lösen und diese Lösung nachvollziehbar darstellen bzw. begründen.
 
 
Probleme mathematisch lösen:
  • Die Schülerinnen und Schüler wenden heuristische Hilfsmittel zum Problemlösen an.
"Die Schülerinnen und Schüler können Lösungsstrategien [...] entwickeln und nutzen heuristische Hilfsmittel zum Problemlösen anwenden" (ebd.)
Bei dieser Aufgabe kann mit einer Skizze des Beetes gearbeitet werden.
 
 
Mathematische Darstellungen verwenden:
  • Die Schülerinnen und Schüler können geeignete Darstellungen zum Lösen der Aufgabe auswählen und nutzen.
"Die Schülerinnen und Schüler können geeignete Darstellungen für das Bearbeiten mathematischer Sachverhalte und Probleme auswählen, nutzen und entwickeln" (RLP, S.20)
Die Schülerinnen und Schüler bearbeiten die Aufgabe anhand einer Skizze.

Heuristische Hilfsmittel: 
  • Bei der zeichnerischen Lösung hilft eine informative Figur weiter. Anhand dieser Figur kann man die Aufgabe eigentlich komplett lösen. Es wird von dem gegebenen rechteckigen Blumenbett ausgegangen, bei dem Länge und Breite um die Hälfte verkürzt werden. Von diesem Startpunkt wird das Blumenbeet mit der Strategie des Vorwärtsarbeitens mithilfe von Mittelsenkrechten aufgeteilt, um anschließend sehen zu können, wie groß die Fläche von Mareike und wie groß die Fläche von Julian ist. Um diese Flächen genauer definieren/bestimmen zu können und aussagekräftiger begründen zu können, warum Mareike sich nicht auf den Deal einlassen sollte, wurde eine zweite informative Figur angelegt. Auch beim rechnerischen Lösungsweg kann man eine Skizze zur Unterstützung der Rechnung erstellen.
 
  • Für die rechnerische Lösung wird auf das heuristische Hilfsmittel der Gleichungen zurückgegriffen. Die Formel der Flächeninhaltsberechnung von Rechtecken ist bekannt. Diese muss nur noch nach den Bedingungen des Deals umgeformt werden, damit die Größe von Mareikes Fläche bestimmt werden kann. Um sich zu vergewissern, ob die Umformung richtig gewesen ist, wird der Lösungsweg anhand von Beispielen - einmal mit umgestellter Gleichung und einmal ohne - Probe gerechnet. Auch hierbei wird wieder die Strategie des Vorwärtsarbeitens angewendet, denn es wird mit den gegebenen Startinformationen gearbeitet, um somit auf den Lösungsweg und das Ergebnis zukommen.
 
 
Heuristische Strategien: 
  • Für die Lösung der Aufgabe ist die heuristische Strategie des kombinierten Vor-und Rückwärtsarbeitens relevant. Zum einen geht man von den gegebenen Bedingungen aus, also der bestimmten Aufteilung des Beetes. Zum anderen aber auch vom Gesuchten, also der Größe des entstandenen Beetes und der Frage, ob es gerecht aufgeteilt wurde. Teilt man also erst das Beet so wie es in der Aufgabe formuliert wird und überlegt dann ob diese Aufteilung gerecht ist, erarbeitet man sich eine Lösung des gestellten Problems.
 
 
Heuristische Prinzipien: 
  • Insbesondere beim ersten Lösungsweg spielt das Zerlegungsprinzip sowie das Invarianzprinzip eine Rolle. So wird das Beet durch die Mittelsenkrechten in vier gleich große Teile geteilt. Somit kann Kenntnis über die Größe von Mareikes Teil erlangt werden. Genauer kann wegen der Tatsache, dass die vier Teilrechtecke gleich groß sind und Julians Teil drei solcher Rechtecke umfasst, Mareikes Teil hingegen nur Eines, gefolgert werden, dass Julians Teil mit dem Deal dreimal so groß ist wie Mareikes. 

Die Garten-Deal-Aufgabe hat nach Cohors-Fresenborg et al einen Schwierigkeitsgrad von *.
 
 
Sprachlogische Komplexität: 
Die Reihenfolge der Sätze entspricht den Schritte der mathematischen Bearbeitung: Zunächst muss Julians Aussage nachvollzogen werden und beim zeichnerischen Lösungsweg der Sachverhalt graphisch dargestellt werden, bzw. beim rechnerischen Lösungsweg das gesamte Beet und Mareikes Teil berechnet werden. Erst dann kann ein Urteil gebildet werden und die anschließende Frage, ob der Deal fair sei, beantwortet werden. Somit lässt sich der Garten-Deal-Aufgabe eine Sprachlogische Komplexität der Stufe 0 zuweisen. 
 
 
Kognitive Komplexität: 
Auch die Kognitive Komplexität entspricht der Stufe 0, da bei allen dargestellten Lösungswegen nur wenige Denkvorgänge nacheinander abzuarbeiten sind.
 
 
Formalisierung von Wissen: 
Bezüglich den zeichnerischen Lösungen ist die Formalisierung von Wissen auf Stufe 0 anzusiedeln, da lediglich graphische Darstellungen zur Lösung der Aufgabe genügen. Bezüglich den rechnerischen Lösungen erfolgt hingegen die Formalisierung von Wissen auf Stufe 1, da bei dieser Lösung mit der Anwendung der Flächeninhaltsformel für Rechtecke sehr einfache Gleichungen aufzustellen sind.  
 
 
Formelhandhabung: 
Die Formelhandhabung entspricht bei der zeicherischen Lösungsvariante der Stufe 0, da bei dieser keine algebraischen Operationen notwendig sind. Bei den rechnerischen Lösungen muss lediglich mit der Flächeninhaltsformel für Rechtecke umgegangen werden, somit entspricht die Formelhandhabung bei diesen Lösungswegen der Stufe 1. 
 
 
Stufenzuordnung: 
Formalisierung von Wissen
Stufe 0
Stufe 1
Formelhandhabung
Stufe 0
Stufe 1
Kognitive Komplexität
Stufe 0
Sprachlogische Komplexität
Stufe 0

Hilfestellungen: 
Aufgrund der offenen Fragestellung könnte es für die Schülerinnen und Schüler schwierig sein, auf die Idee zu kommen, nach welchen Kriterien sie entscheiden (Idee des Vergleichs der Größe von Mareikes Teil mit Julians Teil, bzw. mit dem Flächeninhalt des gesamten Beets), ob sich Mareike auf den Deal einlassen soll. Sollte dieses Problem auftreten, können die folgenden Hilfestellungen gegeben werden.
 
Allgemein-strategische Hilfen Inhaltsorientierte strategische Hilfen Inhaltliche Hilfen
Fertige erst einmal eine Situationsskizze an. Welche mathematische Größe gibt Auskunft über die Größe einer Fläche? Kannst du mithilfe dieser Größe die Aufgabe lösen? Wann hat Mareike Vorteile von dem Deal?
Welche Informationen sind gegeben? Vergleiche doch die Größe von Mareikes Teil und Julians teil. Wann sollte Mareike den Deal annehmen?
Was kannst du mit den gegebenen Informationen berechnen? Welchen Anteil vom gesamten Beet macht Mareikes Teil aus? Ist der Deal fair?
 
 
 
Sozialformen: 
  • Einzelarbeit
  • Partnerarbeit
 
 
Differenzierungsmöglichkeiten: 
Die Aufgabe bietet sowohl leistungsschwächeren Lernenden als auch leistungsstärkeren Schülerinnen und Schülern Differenzierungsmöglichkeiten.
 
So könnte man die Aufgabe für leistungsschwächere Schülerinnen und Schüler folgender Maßen vereinfachen:
  • Man könnte dem Blumenbeet Maße geben. Dies wäre für einige Schülerinnen und Schüler sicherlich schon eine Erleichterung, da sie nicht mit Variablen hantieren müssten, sondern genau wüssten, wie groß die verkürzten Längen und Breiten sind. Alternativ könnte man die Vorgabe der Flächeninhaltsformel anbieten.
 
  • Es könnten dieser Aufgabe ähnliche Aufgaben vorhergestellt werden. Hierbei könnte das Kind, die Lösung der Aufgabe auf eine bereits vorher gelöste Aufgabe, im Sinne eines Analogieschlusses, zurück führen.
 
  • Man könnte die Aufgabe leicht umdrehen. Also erfragen, was Julian für ein Angebot machen könnte, das fair erscheint. Die Kinder müssten also überlegen wie sie die Fläche am besten in zwei Hälften teilen könnten. Dabei würde man unter Umständen Abstand von der Lösung einer Gleichung nehmen, aber die theoretische Auseinandersetzung mit einer Fläche und ihren Eigenschaften fördern.
 
  • Eine andere Differenzierung bestände darin, dass die Schülerinnen und Schüler sich das rechteckige Blumenbeet auf Pappe ausschneiden können, oder sie dies erhalten. Mit einer Schere könnten sie dann die Forderungen des Deals aktiv ausführen und erhalten die Fläche von Mareike als ausgeschnittenes Rechteck, sowie Julians Fläche, in die das Rechteck dreimal hinein passt.
 
  • Allgemein ist es immer hilfreich einen Leitfaden für die Bearbeitung mit Problemlöseaufgaben im Raum hängen zu haben, auf den die Schülerinnen und Schüler bei Unsicherheiten und Problemen zurückgreifen können.
 
  • Eine Vereinfachung kann beispielsweise auch durch Veränderung des Kontextes erfolgen. Die Aufgabe könnte dann lauten:
Julian und Mareike wollen auf ihrem Beet Mohrüben pflanzen. Sie haben dafür eine Beetreihe, welche 100cm lang ist, zur Verfügung. Zwischen jeder Pflanze müssen 10cm frei sein. Wie viele Mohrüben können sie in einer Reihe pflanzen?
 
Lösungsweg 1: 
Rechnung: \(100cm:10cm= 10\)
Antwort: Sie können 10 Mohrüben pflanzen.
 
 
 

Lösungsweg 2:
Rechnung: 1cm auf dem Papier \(\cong \) 10cm auf dem Beet
Antwort: Es können 10 Mohrüben gepflanzt werden. 
 
 
 
 
 
 
 
 
Wird die Aufgabe in diesem Maße umgeformt, erfolgt eine Reduktion von der mathematischen Größe des Flächeninhalts auf die Länge. Es ist nicht mehr notwendig das die Schülerinnen und Schüler mit Einheiten für Flächen umgehen können, sondern nur noch mit Einheiten für Längen. Darüber hinaus müssen die Lernenden kein Urteil über die Fairness des Deals bilden.
 
 
 
Für leistungsstärkere Lernende können folgende Veränderungen bezüglich der Aufgabe vorgenommen werden:
  • Es können Ergänzungsaufgaben gestellt werden. So könnten sie sich nach erfolgreicher Lösung der Aufgabe überlegen, inwieweit der Deal geändert werden müsste, damit er für beide Kinder gerecht wäre. Eine andere Zusatzaufgabe für leistungsstärkere Schülerinnen und Schüler wäre es, wenn sie sich überlegen, wie viele Pflanzen Julian in seinen Teil und wie viele Pflanzen Mareike in ihren Teil pflanzen kann. Hierzu würde es eine Auflistung von unterschiedlichen Pflanzen geben, mit kreisrunder oder quadratischer Grundfläche. Die Lernenden müssten überlegen welche Kombinationen möglich sind, damit am wenigsten unbepflanzte Fläche übrig bleibt. Des Weiteren bietet sich an ergänzend zu fragen: „Gilt dies für alle Seitenlängen a und b?“ Eine Antwort auf diese Zusatzfrage könnte beispielsweise durch die Heuristische Strategie des Systematischen Probierens und im Heuristischen Hilfsmittel der Tabelle erlangt werden. 
 
  • Man könnte Werte für die Fläche vorgeben, die eine Berechnung interessanter machen.
 
  • Daneben könnte man die Schülerinnen und Schüler einen expliziten Gegenvorschlag für einen Deal formulieren lassen. Dieser kann fair sein, aber vielleicht finden sie ja einen Weg es ähnlich fair aussehen zu lassen, obwohl Mareike am Ende mehr bekommt?
 
  • Des Weiteren kann man untersuchen lassen, wie es sich mit einer komplizierteren Gartenform anstellen würde. Sagen wir mal das Gartenstück ist angelegt wie ein Rechteck, an dem an einer kurzen Seite ein Dreieck anliegt. Wie kann man hier gerecht teilen?  
 
  • Die Aufgabe könnte auch wie folgt durch Veränderung des Kontextes schwieriger gestaltet werden:
Julian und Mareike wollen ihr Beet mit Brettern eingrenzen. Das Beet ist 2 m lang und 1 m Breit. Um sich Bretter zu sägen, bekommen sie von ihrem Vater mehrere Holzblöcke zu Verfügung. Diese sind 20 cm lang, 10 cm tief und besitzen ein Volumen von 2000 cm³. Wie hoch ist ein Holzblock? Die Bretter sollen flach auf den Boden gelegt werden und 1 cm hoch sein. Wie viele Blöcke und wie viele Bretter benötigen die Kinder um ihr Beet zu umranden?
 
Beet : Länge = 2 m, Breite = 1 m;
Holzblock: Länge = 20 cm, Tiefe = 10 cm, Volumen = 2000 cm³;
Brett soll 1 cm hoch sein
Höhe des Blockes;
Anzahl der Bretter/Blöcke
gegeben:
 
 

gesucht:
 

Lösungsweg 1:
Rechnung: Umfang des Beetes: \(2+2+1+1=6m\)
Höhe des Blockes: \(2000:20=100, 100:10=10\)
Der Block ist 10 cm hoch.
Aus einem Block gewinnt man 10 Bretter welche 20cm lang sind.
\(600cm:20cm= 30\)
Man benötigt 30 Bretter um das Beet zu umranden.
\(30:10=3\)
Antwort: Für die Bretter benötigt man 3 Blöcke.
 
 
 
 
 
 
 
 
 
 
 
Lösungsweg 2:
Rechnung:
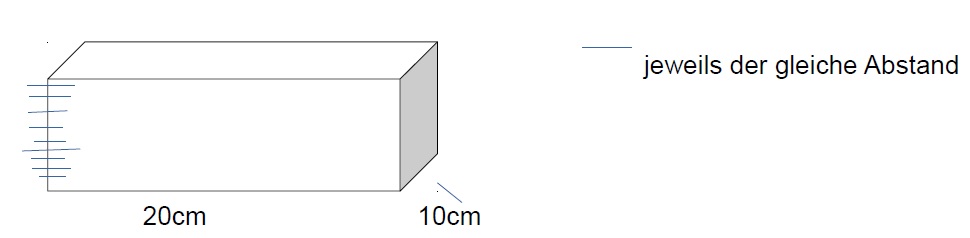Der Block ist 10cm hoch.
Danach folgt eine Rechnung wie bei Lösungsweg 1.
Antwort: Für die Bretter benötigt man 3 Blöcke.
 
 
 
 
 
 
 
 
 
 
 
 
Mit dieser Veränderung der Aufgabe werden von den Schülerinnen und Schüler zusätzlich Kenntnisse über das Volumen eines Quaders abverlangt.

Diese Aufgabe kann in mehrere Lernsituationen eingebettet werden. Am besten eignet sie sich als Aufgabe, mit der produktives Üben gewährleistet werden kann. Die Schülerinnen und Schüler können zum einen die Flächeninhaltsformel des Rechtecks üben und somit ihr Wissen verfestigen. Zum anderen können sie erkennen, dass diese Formel nicht immer nur so zu verwenden ist, wie sie im Formelbuch geschrieben steht. Hierzu sollte der Flächeninhalt und seine Berechnung aber wenigstens schon einmal thematisiert worden sein, weswegen sich ein Einstieg mit Hilfe dieser Aufgabe als schwierig gestaltet, wenn die Schülerinnen und Schüler alleine an ihr arbeiten sollen. Besteht die Möglichkeit, die Aufgabe im Klassenverband zu besprechen, so kann man sie aber auch in der Einstiegsphase nutzen. Dann könnten die Schülerinnen und Schüler versuchen die Aufgabe zu lösen, was viele sicherlich zeichnerisch tun würden, um auf dieser Grundlage im weiteren Stundenverlauf zu thematisieren, wie man die Aufgabe auch rechnerisch hätte lösen können, und welches Verfahren/welche Formel dabei zum Einsatz kommt.
 
Darüber hinaus kann die Aufgabe auch verwendet werden, damit die Schülerinnen und Schüler auf leichtem Niveau Beweisen üben können, indem sie durch Proben und Gegenrechnungen zeigen, dass ihre aufgestellte Gleichung zur Berechnung von Mareikes Teil wiederspruchsfrei das gleiche Ergebnis liefert. Außerdem könnte das Beweisen dadurch geübt werden, dass man den Lernenden die Aufgabe gibt, aus der Sicht von Mareike zu argumentieren und eine bessere Lösung zu finden. Diese müsste dann natürlich auch bewiesen werden. 


Bearbeitet von: Josephine Crome, Lele Lucas, Chantalle Mundt, Tobias Ruderer, Elisa Schmidt (überarbeitet von Marisa Pfläging)
nach oben
397 Nutzer/-innen haben abgestimmt.

Feedback

Wir freuen uns auf Ihre Anregungen und konstruktive Rückmeldung zum Material.