Geometrische Denkaufgabe Raute

Klasse Schulstufe Thema Themengebiet Schwierigkeit
8/ 9/ 10 Sekundarstufe I Begründen in der ebenen Geometrie Raum und Form **

Aufgabenstellung

 
Das Rechteck ABCD hat folgende Eigenschaften: \(\overline { AB }=111, \overline{DA} = \overline{PB}=\overline{QD}=70\)
Ist PRQS eine Raute?
Claudia und Claus diskutieren. Claudia meint: „ Klar ist das eine Raute, das sieht man doch.“
Claus: „Ich bin mir da nicht so sicher, vielleicht sollten wir es mal versuchen auszurechnen.“
 
 

Quellenangabe:

Original aus Eigenmann, P. (1981). Geometrische Denkaufgaben. Stuttgart: Klett.


Lösungsvariante 1
 
Zuerst werden die gegebenen Informationen aus der Aufgabenstellung entnommen:
  • ABCD ist ein Rechteck, d.h. alle Innenwinkel sind rechte Winkel (90°).
  • Die Strecke \(\overline { AB } \)  ist 111 lang.
  • Die Strecken \(\overline { AD }, \overline {BP} \) und \(\overline{DQ}\)  sind 70 lang.
 Um zu erkennen, welche Strecken für die Lösung relevant sind, ist es von Vorteil die Streckenlängen in der Skizze zu ergänzen.
 
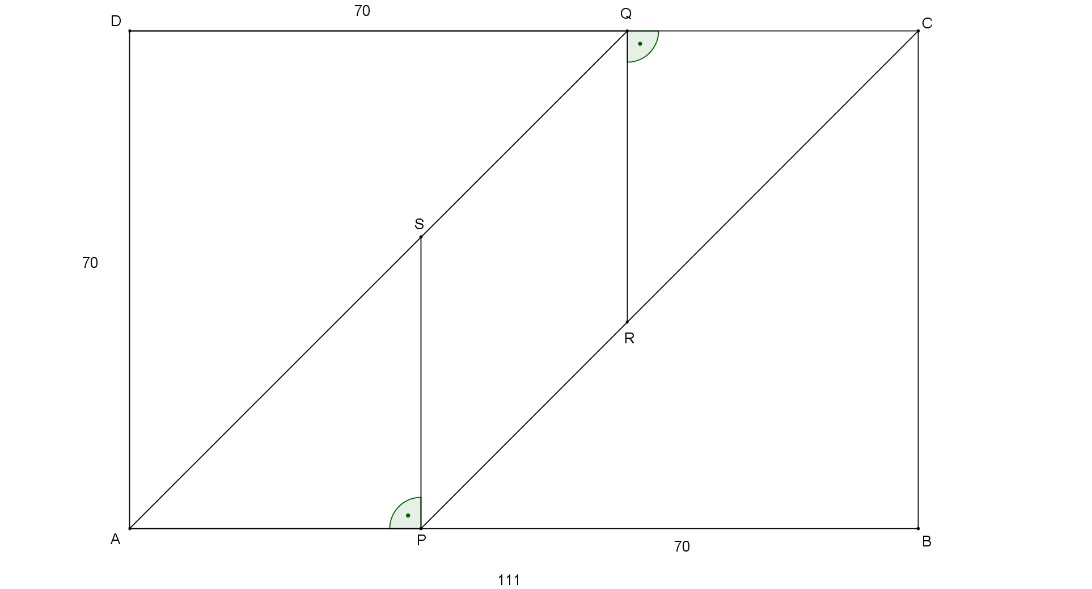
Die Streckenlänge \(\overline { AB } \) ergibt sich aus der Summe \(\overline { AP } \) und \(\overline { PB } \). Daraus ergibt sich für \(\overline { AP } =\overline { AB } -\overline { PB } =111-70=41\).
Analog ergibt sich für \(\overline { CQ } =41\), da \(\overline {CD}\) ebenfalls 111 lang ist. Dies wiederum ergibt sich aus der Eigenschaft eines Rechtecks, dessen gegenüberliegende Seiten gleich lang sind.
 
Eine Raute ist ein gleichseitiges Viereck, bei dem die gegenüberliegenden Seiten parallel und die gegenüberliegenden Winkel gleich groß sind. Diese Eigenschaften sind nun also beim Viereck PRQS zu überprüfen.
 
 
 
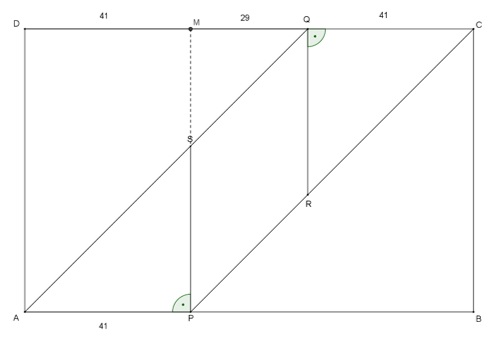
Erzeuge einen Hilfspunkt M durch Verlängerung der Strecke \(\overline { PS } \). Mit \(\overline { PM } \) senkrecht auf \(\overline { AP } \)(und auf \(\overline { QD } \)) ergibt sich \(\overline { MD }=41 \). Somit ist \(\overline { QM } =\overline { QD } -\overline { MD } =29\) lang. Da \(\overline { DA } =\overline { QD } \) und \(\sphericalangle QDA=90°\) ergibt sich wegen \(\triangle AQD\) rechtwinklig- gleichschenklig \(\sphericalangle AQD=45°\). Mit der Innenwinkelsumme im Dreieck ergibt sich für \(\sphericalangle MSQ=45°\). Somit ist \(\triangle MSQ\) rechtwinklig-gleichschenklig und \(\overline { MS } =29\) und \(\overline { PS } =\overline { DA } -\overline { MS } =41\). Zur Ermittlung der Streckenlänge \(\overline { SQ } \) kann nun der Satz des Pythagoras genutzt werden. Damit ergibt sich \({ \overline { SQ } }^{ 2 }={ \overline { MS } }^{ 2 }+{ \overline { QM } }^{ 2 }=29²+29²=1682\). Somit ist \(\overline { SQ } \approx 41,01219331\) lang. Da \(\overline { SP } \neq \overline { SQ } \) ist PRQS keine Raute.
 
 
 
 
Lösungsvariante 2
 
Eine zweite Möglichkeit die Lösung der Aufgabe zu finden, wäre eine Modellierung mittels dynamischer Geometriesoftware.
Dabei liegt dann allerdings nicht mehr der Fokus auf dem schlüssigen Argumentieren, sondern eher auf dem Üben der Nutzung von dynamischer Geometriesoftware. Nachdem die Skizze mit allen erforderlichen Maßen zum Beispiel in Geogebra erstellt wurde, lässt sich schnell durch das Messen der verschiedenen Seitenlängen herausfinden, dass diese nicht alle gleich lang sind. Vorraussetzung für ein korrektes Ergebnis ist jedoch eine korrekte Konstruktion. Mittels GeoGebra ist diese mithilfe der vorhandenen Werkzeuge nicht immer trivial zu erhalten. Hier müssen zum Beispiel parallele Geraden erzeugt werden, oder bestimmte Schnittpunkte gesetzt werden. Auch ist die Interpretation des Ergebnisses wichtig. So ist eben das Ergebnis 41,01 kein Resultat von gerundeten Werten. Bei dieser Lösungsvariante müsste sich eine sinnvolle Disskussion des Ergebnisses anschließen. Möglicherweise führt diese dann zum ersten Lösungsweg und der Erkenntnis, dass eine lückenlose Argumentation zu gleichem Ergebnis führt. Eine Anwendung des Satzes des Pythagoras ist bei der Lösung mittels dynamischer Geometriesoftware nicht gleich ersichtlich. Intern wird die Software diesen jedoch vermutlich nutzen.

Die geometrische Denkaufgabe Raute kann im Rahmen der Unterrichtssequenz zur Satzgruppe des Pythagoras in der siebten Klasse an Gymnasien thematisiert werden. Denn die erforderlichen Kompetenzen der Schülerinnen und Schüler zur Lösung dieser Aufgabe liegen höchstens auf der Niveaustufe E (vgl. Abschnitt "Geförderte Kompetenzen"), was der siebten Jahrgangsstufe an Gymnasien entspricht.
 
Für die Bearbeitung sind Kenntnisse über den Umgang mit Skizzen, über allgemeine Winkelbeziehungen und über die Winkelsumme im Dreieck sowie Kenntnisse über spezielle Dreiecke erforderlich. Der Satz des Pythagoras sollte bereits eingeführt worden sein, sodass die Schülerinnen und Schüler diesen in der Aufgabe anwenden und üben können.
 
Mit der Aufgabe kann bereits erlerntes Wissen über Rechtecke, Rauten sowie Winkelbeziehungen mit dem neu erlerntem Wissen über den Satz den Pythagoras verknüpft werden. Die geometrische Denkaufgabe hat demnach auch eine Wiederholungsfunktion. Außerdem kann verdeutlicht werden, dass der Satz des Pythagoras nicht nur in Bezug auf direkte Berechnungen an rechtwinkligen Dreiecken von Bedeutung ist, sondern darüber hinaus auch sinnvoll sein kann, um andere Sachverhalte in der Mathematik zu beweisen. Den Schülerinnen und Schüler kann somit ein Ausblick über die Mathematik als Wissenschaft gegeben werden. (Sätze und Definitionen werden angewandt, um weitere Sätze zu verifizieren/ Mathematik als abstraktes Konstrukt aus Sätzen und Definitionen) Dies kann allerdings besser verdeutlicht werden, wenn die Aufgabe als Beweisaufgabe formuliert wird und wenn für die Seiten allgemeine Bezeichnungen verwendet werden und keine Zahlen.

Inhaltsbezogene Kompetenzen
 
Raum und Form
  • Die Schülerinnen und Schüler kennen die Eigenschaften eines Rechtecks und beschreiben diese.
Um die Aufgabe lösen zu können, benötigen die Schülerinnen und Schüler genaue Kenntnisse über die Eigenschaften der geometrischen Figur Rechteck. So ist es für den Lösungsweg unerlässlich zu wissen, dass alle Innenwinkel des Rechtecks rechte Winkel sind. Daraus abgeleitet ergibt sich ebenfalls noch die Eigenschaft, dass die gegenüberliegenden Seiten eines Rechtecks gleich lang und parallel sind.
 
  • Die Schülerinnen und Schüler kennen die Eigenschaften einer Raute und beschreiben diese.
Um eine Idee zu bekommen, welche Strecken die Lernenden untersuchen müssen, ist es ebenfalls notwendig die geometrische Figur Raute in der Zeichnung zu erkennen. Weiterhin müssen die Schülerinnen und Schüler wissen, welche Eigenschaften eine Raute besitzt. Denn dies mündet in den zu untersuchenden Sachverhalt. Es ist zu prüfen, ob alle vier Seiten der Raute gleich lang sind.
 
Diese Kompetenzen sollten die Schülerinnen und Schüler laut brandenburgischem RLP spätestens in der 6. Klasse an Gymnasien erlangt haben.
Raum und Form, Niveaustufe D "Die Schülerinnen und Schüler können weitere geometrische Objekte qualitativ beschreiben"(RLP, S.26), sie können "[...] ebene geometrische Figuren zeichnen" (ebd), wobei beispielsweise Kenntnisse über die Eigenschaften einer Raute Voraussetzung sind.

Eine weitere Kompetenz, die bei der Lösung der Aufgabe von Bedeutung ist und in der siebten Gymnasialjahrgangsstufe erworben werden sollte, ist die folgende:
  • Die Schülerinnen und Schüler kennen den Innenwinkelsummensatz bezüglich eines Dreiecks.
Raum und Form, Niveaustufe E "Die Schülerinnen und Schüler können Beziehungen zwischen geometrischen Objekten beschreiben (auch Sätze über Dreiecke)" (RLP, S.26)
 
 
Größen und Messen
  • Die Schülerinnen und Schüler verwenden den Satz des Pythagoras zur Berechnung von Streckenlängen in rechtwinkligen Dreiecken.
Zur Lösung der Aufgabe müssen die Lernenden den Satz des Pythagoras anwenden. Um dies tun zu können, müssen sie die Vorrausetzungen für die Anwendung überprüfen. So müssen sie erst begründen, dass das Dreieck rechtwinklig ist, um dann den Satz anwenden zu können. Dies setzt voraus, dass die Schülerinnen und Schüler die Bedingungen kennen und wissen, dass diese im Vorfeld zu prüfen sind.
Raum und Form, Niveaustufe E "Die Schülerinnen und Schüler können Beziehungen zwischen geometrischen Objekten beschreiben (auch Sätze über Dreiecke)" (RLP, S.26);
Größen und Messen, Niveaustufe E "Die Schülerinnen und Schüler können Größen messen und Maße aus ausgewählten
Darstellungen entnehmen" (RLP, S.24)
 
 
 
Prozessbezogene Kompetenzen
 

Mathematische Darstellungen verwenden

  • Die Schülerinnen und Schüler verändern die Zeichnung in der Aufgabenstellung zielgerichtet.
Um auf eine Lösungsidee zu kommen, ist es notwendig, dass die Schülerinnen und Schüler die in der Aufgabenstellung gegebene mathematische Darstellung zielgerichtet verändern. Dazu zählt das Ergänzen der Streckenlängen an den jeweiligen Strecken. Außerdem müssen die Lernenden erkennen, dass sie für die Berechnung der einen Seite der Raute ein Hilfsdreieck benötigen. Dieses erhalten sie nur, wenn sie die Zeichnung durch eine weitere Strecke ergänzen. Dabei muss die Ergänzung so gewählt werden, dass sie auch zielführend ist.
Mathematische Darstellungen verwenden [K4] "Die Schülerinnen und Schüler können geeignete Daratellungen [...] nutzen und entwickeln" (RLP, S.20), sie können "Darstellungen zielgerichtet verändern" (ebd.)
 
 
Mathematisch argumentieren
  • Die Schülerinnen und Schüler erbringen eine mehrschrittige Argumentation zur Begründung ihrer Lösung.
Die Lernenden begründen jeden ihrer Lösungsschritte durch mathematische Sachverhalte. Sie erstellen dabei eine lückenlose Folgerungskette. So muss zum Beispiel erst begründet werden, warum ein Teildreieck rechtwinklig ist, bevor der Satz des Pythagoras genutzt werden kann. Hierbei ist es wichtig auch augenscheinlich eindeutige Sachverhalte mathematisch zu begründen.
Mathematisch argumentieren [K1] "Die Schülerinnen und Schüler können Begründungen [...] zunehmend selbstständig ermitteln" (RLP, S.19), sie können "mehrschrittige Argumentationen zur Begründung und zum Beweisen mathematischer Aussagen entwickeln" (ebd.)
 
 
Probleme mathematisch lösen
  • Die Schülerinnen und Schüler wenden eine informative Figur zum Problemlösen an.
Um auf eine Lösungsidee zu kommen, ist es notwendig die Zeichnung aus der Aufgabenstellungen so zu verändern, dass daraus bereits erahnt werden kann, welche Strecken für die Lösung des Problems relevant sind. So kann durch das Ergänzen der Streckenlängen in der Skizze bereits abgeleitet werden, welche Strecken gesucht bzw. zu berechnen sind.
Probleme mathematisch lösen [K2] "Die Schülerinnen und Schüler können heuristische Hilfsmittel zum Problemlösen anwenden" (RLP, S.19), sie können "mathematische Kenntnisse, Fähigkeiten und Fertigkeiten bei der Bearbeitung von Problemen anwenden" (ebd.) sowie "Zusammenhänge erkennen undLösungsstrategien auf ähnliche Sachverhalte übertragen" (ebd.)

Heuristische Hilfsmittel: 
  • Den Schülerinnen und Schülern ist bereits mit der Aufgabenstellung eine Skizze gegeben, welche darstellt, um was es in der Aufgabe geht. Durch Veränderung dieser Skizze wird immer anschaulicher, wie die Lernenden zur Lösung gelangen können. Es handelt sich dabei um eine Informative Figur.   
 
  • Mithilfe von Gleichungen berechnen die Schülerinnen und Schüler die jeweils gesuchten Strecken. Außerdem wird der Satz des Pythagoras und der Innenwinkelsummensatz des Dreiecks verwendet. Somit spielen Gleichungen bei der Lösung des Problems eine Rolle.
 
 
Heuristische Strategien: 
  • Bei der Lösung der Aufgabe wird zunächst vom Gegebenen ausgegangen und durch Ergänzung dieser Informationen in der Skizze wird versucht eine Lösung zu finden. Gleichzeitig wird die Skizze aber auch ausgehend vom Gesuchten betrachtet, da ja überhaupt erst einmal herausgestellt werden muss, welche Bedingungen genau erfüllt sein müssen, damit das Rechteck eine Raute ist. Somit handelt es sich beim Lösen des Problems um ein Kombiniertes Vorwärts- und Rückwärtsarbeiten.
 
  • Durch Konstruktion des Hilfspunktes M wird das Anwenden des Satzes des Pythagoras ermöglicht. Durch diese Konstruktion wird von Unbekanntem auf Bekanntes rückgeführt und Analogieschlüsse werden ermöglicht.
 
 
Heuristische Prinzipien: 
  • Durch Ergänzung des Hilfspunktes M wird das gleichschenklige rechtwinklige Dreieck \(\triangle AQD\) in das gleichschenklige rechtwinklige Dreieck \(\triangle SQM\) und das Viereck ASMD zerlegt. Außerdem wird dadurch die Strecke \(\overline { QD } \) in die Strecken \(\overline { QM } \) und \(\overline {MD}\) zerlegt sowie die Strecke \(\overline {DA}\) in \(\overline {MS}\) und \(\overline {SP}\). Dies ist für die weitere Lösung hilfreich. Somit wird das Zerlegungs- und Ergänzungsprinzip verwendet.
 
  • Das Invarianzprinzip ist bei der Berücksichtigung gleichlanger Streckenabschnitte und bei Argumentation mit gleichschenkligen Dreiecken von Bedeutung.
 
  •  Das Transformationsprinzip wird beim algebraischen Formalisieren der Strecken angewandt.

Die Geometrische Denkaufgabe Raute wird aufgrund der 4 vergebenen Punkte nach Cohors-Fresenborg der Stufe ** zugeordnet.
 
 
Sprachlogische Komplexität: 
Die Aufgabenstellung besteht aus mehreren Haupt- und Nebensätzen, wobei nur zwei Hauptsätze die eigentliche Fragestellung beinhalten. Der Rest der Aufgabenstellung dient lediglich dazu klarzumachen, dass eine intuitive Beantwortung nicht ausreichend ist. Im ersten Satz werden weitere Informationen zur Zeichnung gegeben. Insgesamt entspricht die Reihenfolge der Satzteile nicht unmittelbar den Schritten der mathematischen Bearbeitung, da der Lösungsweg nicht vorgegeben wird. Eine Vorstellung von dem, was in der Aufgabe gefordert ist, ist jedoch relativ leicht verständlich. Aufgrund dieser Beobachtungen kann man die Aufgabenstellung hinsichtlich der sprachlogischen Komplexität der Stufe 1 zuordnen.

 

 

Kognitive Komplexität: 
Zur Lösung der Aufgabe muss die Auswahl der Denkvorgänge der Durchführung einzelner Schritte vorausgehen, da zu überlegen ist, welche Größen zunächst ermittelt werden müssen, um zu entscheiden, ob PRQS eine Raute ist. Dazu sind heuristische und strategische Überlegungen (vgl. Abschnitt "Heurismen") notwendig. Darum wird die Aufgabe bezüglich ihrer kognitiven Komplexität der Stufe 2 zugeordnet.

 

 

Formalisierung von Wissen: 
Zur Lösung der Aufgabe müssen einfache formale Darstellungen verstanden werden. So muss zum Beispiel verstanden werden, dass \(\overline {AB} = 111\) \(\overline{AB}=111\)für die Streckenlänge der Strecke \(\overline{AB}\)\(\overline {AB}\) steht. Weiterhin ist das Symbol für den rechten Winkel (Punkt im Viertelkreis) zu interpretieren als eine Winkelangabe von 90°. Aufgrund der einfachen Darstellungen, die in der 7/8 Jahrgangsstufe bereits bekannt sein sollten, wird die Aufgabe hinsichtlich der Formalisierung von Wissen in Stufe 1 eingestuft.
 
 
Formelhandhabung: 
Für eine rechnerische Lösung der Aufgabe müssen die Subtraktion sowie das Quadrieren beherrscht werden, was mindestens der Stufe 1 hinsichtlich des Aspektes der Formelhandhabung entspricht. Allerdings sind die durchzuführenden Rechnungen naheliegend und weisen nicht viele Schritte auf, sodass eine Vergabe der Stufe 2 zu hoch gegriffen wäre. Folglich wird für diese Aufgabe bezüglich der Formelhandhabung aus der Perspektive einer rechnerischen Lösung die Stufe 1 vergeben.
 
 
Stufenzuordnung: 
Formalisierung von Wissen
Stufe 1
Formelhandhabung
Stufe 1
Kognitive Komplexität
Stufe 2
Sprachlogische Komplexität
Stufe 1

Hilfestellungen: 
Zu erkennen, dass für die Lösung der Aufgabe eine Hilfsgerade eingezeichnet werden muss, aus der man einen Hilfspunkt M erhält, ist vermutlich die größte Hürde bei dieser Aufgabe. Um die Schülerinnen und Schüler bei der Findung dieser Idee zu unterstützen, können folgende Hilfestellungen angeboten werden.
 
allgemein-strategische Hilfestellungen inhaltsorientierte-strategische Hilfestellungen inhaltliche Hilfestellungen
Unterstreiche das Wichtige. Gibt es Hilfslinien, die dir weiterhelfen könnten? Welche Eigenschaften hat eine Raute?
Wie beginnen wir bei Problemlöseaufgaben? Welche Größen kannst du in die Skizze eintragen, die dir helfen, die Aufgabe zu lösen? Suche dir gleichschenklig rechtwinklige Dreiecke. Was weist du über deren Seitenlängen?
Was ist gegeben und was wird gesucht? Kannst du bekannte Sätze über Dreiecke anwenden? Verlängere die Strecke \(\overline {PS}\) \(\overline {PS}\) um einen Hilspunkt zu erhalten.
 
 

Neben der vorangegangen erwähnten Problematik der Hilfslinie, könnte auch bereits das Finden eines Lösungsansatzes problematisch sein. Um den Schülerinnen und Schülern hier einen Anstoß zu geben, wären folgende Hilfestellungen möglich.
 
allgemein-strategische
Hilfestellungen
 inhaltsorientierte-strategische Hilfestellungen inhaltliche Hilfestellungen
Erinnere dich an ähnliche Aufgabenstellungen. Welche Winkel kannst du in die Skizze eintragen? Welche Eigenschaften hat ein Rechteck?
Wie beginnen wir bei Problemlöseaufgaben? Welche Größen kannst du in die Skizze eintragen? Was weißt du über die Innenwinkelsumme von Dreiecken?
Was ist gegeben? Kannst du bekannte Sätze über Dreiecke anwenden? Welche Streckenlängen kannst du berechnen?
 
 
 
Sozialformen: 
Die Aufgabe kann in Einzelarbeit bearbeitet werden, oder wie die Aufgabenstellung bereits nahelegt auch in Partnerarbeit diskutiert werden.
 
 
 
Differenzierungsmöglichkeiten: 
Für leistungsschwächere Schülerinnen und Schüler kann die Geometrische Denkaufgabe Raute wiefolgt verändert werden:
 
Vereinfachung durch Ergänzung einer Lösungsidee im Dialog:
 
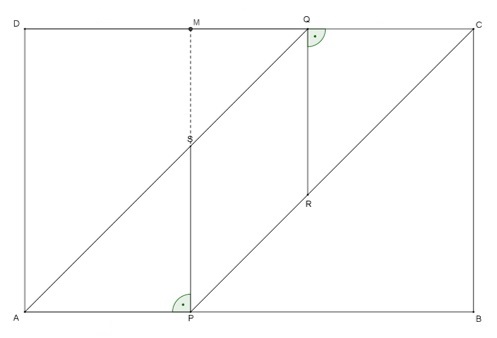
Das Rechteck ABCD hat folgende Eigenschaften: \(\overline { AB }=111, \overline{DA} = \overline{PB}=\overline{QD}=70\)\(\overline { AB }=111, \overline{DA} = \overline{PB}=\overline{QD}=70\)
Ist PRQS eine Raute?
Kim und Claus diskutieren. Kim meint: „Klar ist das eine Raute, das sieht man doch.“
Claus: „Ich bin mir da nicht so sicher, vielleicht sollten wir es mal versuchen
           auszurechnen.“
Kim: „Hmm, und wie willst du das machen?“
Claus: „Wir können doch den Hilfspunkt M einzeichnen und dann überprüfen, ob die   
          Seitenlängen des Vierecks PRQS gleich lang sind.“
 
Hier wird der Lösungsansatz im Dialog gegeben, wodurch die oben genannte Schwierigkeit auf die Idee zu kommen eine Hilfslinie einzuzeichnen, aus dem man einen Hilfspunkt erhält, umgangen wird. Den leistungsschwächeren Schülerinnen und Schülern wird somit ein Zugang zur Aufgabe geschaffen.
Bei dieser Änderung wurde auch der Name für Claudia geändert, da sonst der Eindruck erweckt werden könnte, dass Claudia als Mädchen weniger Ahnung als Claus hat. Der Name Kim kann sowohl einen Mann als auch eine Frau darstellen.
 
Vereinfachung durch Hinweise im Dialog:
Das Rechteck ABCD hat folgende Eigenschaften: \(\overline { AB }=111, \overline{DA} = \overline{PB}=\overline{QD}=70\)\(\overline { AB }=111, \overline{DA} = \overline{PB}=\overline{QD}=70\)
Ist PRQS eine Raute?
Kim und Claus diskutieren. Kim meint: „Klar ist das eine Raute, das sieht man doch.“
Claus: „Ich bin mir da nicht so sicher, vielleicht sollten wir es mal versuchen
           auszurechnen.“
Kim: „Na gut, dann lass uns das überprüfen. Wir werden ja sehen.“
Claus lacht: „Ok, die rechtwinkligen Dreiecke helfen uns bestimmt bei der Lösung.  
                  Wir könnten den Satz des Pythagoras anwenden.“
 
Hier wird den Schülerinnen und Schülern der zusätzliche Hinweis gegeben, dass der Satz des Pythagoras angewandt werden kann.
 
 
Für leistungsstärkere Schülerinnen und Schüler kann die Aufgabe wiefolgt geändert werden:
 
Veränderung durch Entkleidung (Weglassen des Dialoges):
Das Rechteck ABCD hat folgende Eigenschaften: \(\overline { AB }=111, \overline{DA} = \overline{PB}=\overline{QD}=70\)\(\overline { AB }=111, \overline{DA} = \overline{PB}=\overline{QD}=70\)
Ist PRQS eine Raute?
 
Hier müssen die Schülerinnen und Schüler zusätzlich erkennen, dass sie ein Ergebnis nicht aus der Skizze erkennen können, sondern nachrechnen müssen.
 
Veränderung durch Ersetzen der Frage und Entkleidung:
Das Rechteck ABCD hat folgende Eigenschaften: \(\overline { AB }=111, \overline{DA} = \overline{PB}=\overline{QD}=70\)\(\overline { AB }=111, \overline{DA} = \overline{PB}=\overline{QD}=70\)
Was ist PRQS für eine geometrische Figur? Begründe dies.
 
Durch diese Verallgemeinerung der Frage, müssen sich die Schülerinnen und Schüler zunächst die verschiedenen Arten von Rechtecken und die jeweiligen Eigenschaften in Erinnerung rufen. Wie bei der vorherigen Änderung müssen die Schülerinnen und Schüler auch hier darauf kommen, dass eine genaue Lösung nur rechnerisch erfolgen kann.
 
Veränderung durch Verallgemeinerung:
Im Rechteck ABCD sind \(\overline { AB }, \overline{DA} = \overline{PB}=\overline{QD}\)\(\overline {AB}\) und \(\overline {DA} = \overline {PB} \) gegeben.
Ist PRQS eine Raute?
Kim und Claus diskutieren. Kim meint: „Klar ist das eine Raute, das sieht man doch.“
Claus: „Ich bin mir da nicht so sicher, vielleicht sollten wir es mal versuchen
           auszurechnen.“
 
Die Lösung dieser Aufgabe erfordert Abstraktionsvermögen der Schülerinnen und Schüler. Darüber hinaus benötigen sie hier Kompetenzen im Umformen von Gleichungen, diese vermutlich in der siebten Klasse noch nicht haben.

Die Aufgabe lässt sich als Problemlöseaufgabe in Klasse 7, nachdem der Satz des Pythagoras behandelt wurde, durchführen. Durch den unmittelbaren Einsatz dieser Übungsaufgabe in diesem Themengebiet haben die Schülerinnen und Schüler direkt einen Anhaltspunkt, welchen Sachverhalt sie dabei nutzen müssen. Gleichzeitig werden die Bedeutung und die Verwendbarkeit des Satzes des Pythagoras geübt.
 
Möglich wäre auch der Einsatz als Hausaufgabe, bei der anschließend die Lösung im Unterricht diskutiert wird. Dabei könnte man dann gesteigerten Wert auf die korrekte und lückenlose Argumentationsweise legen.
 

 


Bearbeitet von: Sebastian Wählt (überarbeitet von Marisa Pfläging)
nach oben
516 Nutzer/-innen haben abgestimmt.

Feedback

Wir freuen uns auf Ihre Anregungen und konstruktive Rückmeldung zum Material.