Geometrische Denkaufgabe: Winkeldetektiv 1

Fehlermeldung

Deprecated function: The each() function is deprecated. This message will be suppressed on further calls in FieldCollectionItemEntity->fetchHostDetails() (Zeile 313 von /www/htdocs/w0127817/beta.proffi-m.de/sites/all/modules/field_collection/field_collection.entity.inc).
Klasse Schulstufe Thema Themengebiet Schwierigkeit
5/ 6/ 7/ 8 Sekundarstufe I Winkel in ebenen Figuren bestimmen Größen und Messen *, **

Aufgabenstellung

Quellenangabe:

Eigenmann, P. (1981). Geometrische Denkaufgaben. Stuttgart: Klett.


Zeichnerische Lösung:

Zeichne einen Kreis mit dem Mittelpunkt A.
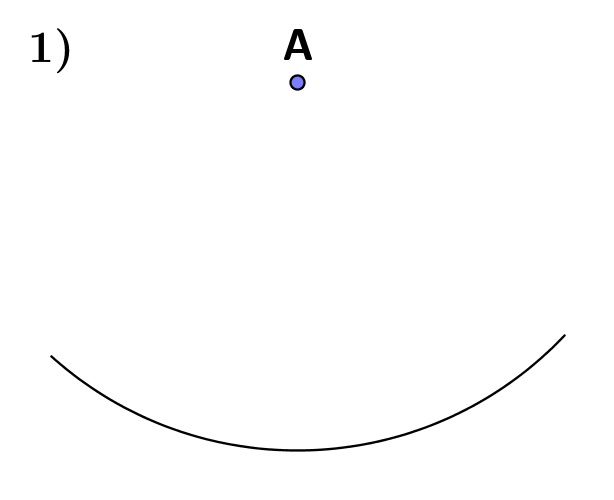Verbinde den Mittelpunkt des Kreises A mit einem Punkt B auf der Kreislinie.
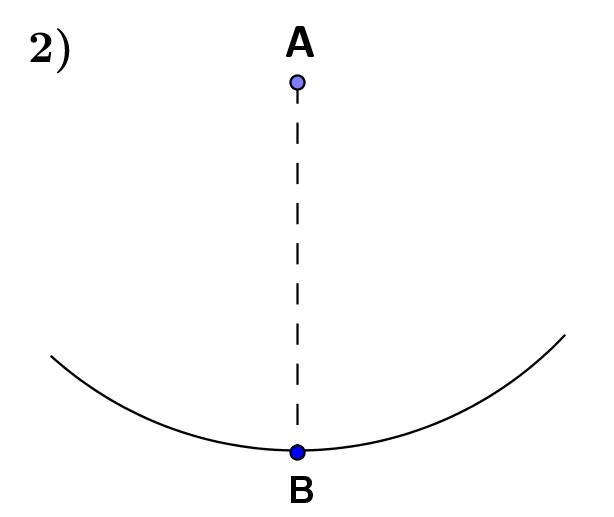Zeichne am Punkt A von beiden Seiten an die Strecke \(\overline{AB}\) jeweils einen Winkel von 22° ein und verbinde den Punkt A in diesem Winkel auf beiden Seiten mit zwei Punkten C und D auf der Kreislinie.

Entferne nun die Strecke \(\overline{AB}\), sodass sich am Punkt A der Winkel \(\gamma\) mit  \(\gamma=44°\) ergibt.
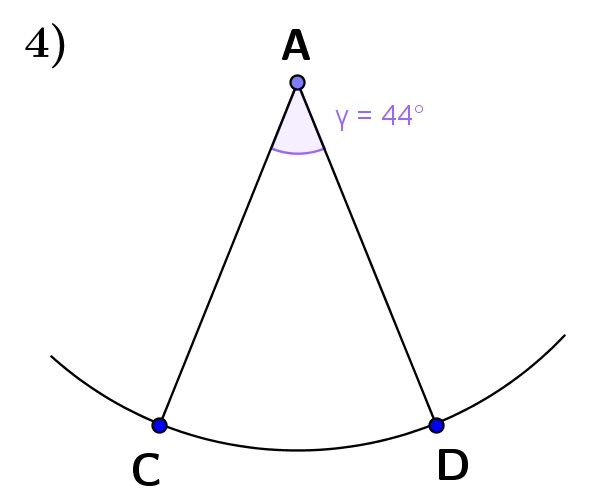Verbinde die Punkte C und D.
Verbinde den Punkt C mit dem Schnittpunkt, der auf der Strecke \(\overline{AD}\) entsteht, wenn man eine zur Strecke \(\overline{AD}\) senkrechte Gerade durch den Punkt C zeichnet.
Zeichne die Winkelhalbierende des Winkels ACD ein.
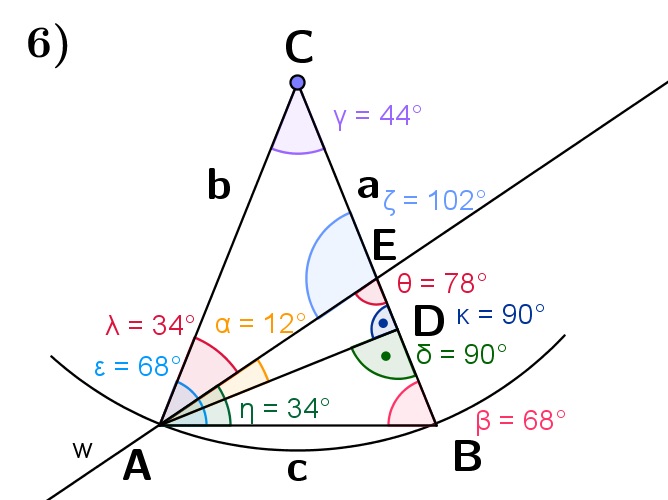
Die Konstruktion führt zu der vorgegebenen Figur. Die gesuchte Größe des Winkel \(\varepsilon\) kann deswegen durch Nachmessen ermittelt werden. Der Winkel \(\alpha\) ist 12° groß.

Rechnerische Lösung 1:

Die Seiten a und b des Dreiecks ABC sind gleich lang, da beide Radien des angedeuteten Kreises darstellen. Demnach handelt es sich bei dem Dreieck ABC um ein gleichschenkeliges Dreieck, woraus folgt, dass die beiden Winkel \(\varepsilon\) und \(\beta\) gleich groß sein müssen.

Aus dem Satz über die Summe der Innenwinkel eines Dreiecks folgt für die Größe der beiden Winkel \(\varepsilon\) und \(\beta\):

\(\varepsilon=\beta=\frac{180°-\beta}{2}=\frac{180°-44°}{2}=\frac{136°}{2}=68°\)

Die Winkelhalbierende w teilt den Winkel \(\varepsilon\), für den gilt: \(\varepsilon=68°\), in die beiden Winkel \(\lambda\) und \(\eta\), wobei gilt:

\(\lambda=\eta=\frac{\varepsilon}{2}=\frac{68°}{2}=34°\)

Für den Winkel \(\zeta\) im Dreieck ABD gilt wegen des Satzes über die Summe der Innenwinkel in einem Dreieck:

\(\zeta=180°-\delta-\beta=180°-90°-68°=22°\)

Mit dem Wissen über die Größen der Winkel \(\eta\) und \(\zeta\) kann die gesuchte Größe des Winkels \(\alpha\) ermittelt werden:

\(\alpha=\eta-\zeta=34°-22°=12°\)

Rechnerische Lösung 2:

Die Seiten a und b des Dreiecks ABC sind gleich lang, da beide Radien des angedeuteten Kreises darstellen. Demnach handelt es sich bei dem Dreieck ABC um ein gleichschenkeliges Dreieck, woraus folgt, dass die beiden Winkel \(\varepsilon\) und \(\beta\) gleich groß sein müssen.

Aus dem Satz über die Summe der Innenwinkel eines Dreiecks folgt für die Größe der beiden Winkel \(\epsilon\) und \(\beta\):

\(\varepsilon=\beta=\frac{180°-\gamma}{2}=\frac{180°-44°}{2}=\frac{136°}{2}=68°\)

Die Winkelhalbierende w teilt den Winkel \(\varepsilon\), für den gilt: \(\varepsilon=68°\), in die beiden Winkel \(\lambda\) und \(\eta\), wobei gilt:

\(\lambda=\eta=\frac{\varepsilon}{2}=\frac{68°}{2}=34°\)

Wegen des Satzes über die Summe der Innenwinkel in einem Dreieck gilt für den Winkel \(\zeta\) im Dreieck AEC:

\(\zeta=180°-\gamma-\lambda=180°-44°-34°=102°\)

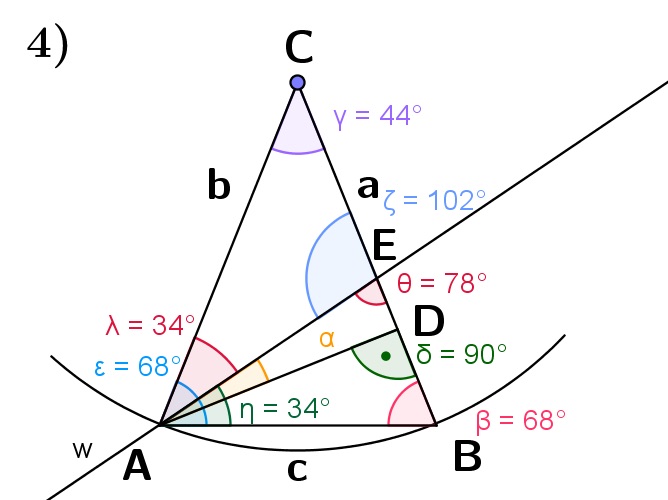
Da der Winkel \(\theta\) der Nebenwinkel zu dem Winkel \(\zeta\) ist, für den gilt: \(\zeta=102°\), gilt für den Winkel \(\theta\):

\(\theta=180°-\zeta=180°-102°=78°\)

Da der Winkel \(\kappa\) der Nebenwinkel zu dem Winkel \(\delta\) ist, für den gilt: \(\delta=90°\), gilt für den Winkel \(\kappa\):

\(\kappa=180°-\delta=180°-90°=90°\)

Wegen des Satzes über die Summe der Innenwinkel eines Dreiecks gilt für den Winkel \(\alpha\) im Dreieck ADE:

\(\alpha=180°-\kappa-\theta=180°-90°-78°=12°\)

Kommentar

Bei der zeichnerischen Variante geht es für die Schüler darum, ein Konstruktionsproblem zu lösen. Anhand der Zeichnung müssen die Schüler eine Konstruktion „herauslesen“ bzw. entwickeln. Es ist zunächst zu erkennen, wie man die Konstruktion beginnt und welche Konstruktionsschritte sich anschließen müssen, um das Konstruktionsproblem lösen zu können und abschließend den Winkel \(\alpha\) ausmessen zu können. Die zeichnerische Variante fördert also anhand eines geometrischen Konstruktionsproblems die Problemlösefähigkeit der Schüler.

Für die rechnerische Variante spricht im Vergleich zur zeichnerischen Variante, dass hier, ausgehend vom Gegebenen durch geeignete Überlegungen ein exakter Wert für den Winkel gefunden werden kann. Zudem werden verschiedene grundlegende Kenntnisse in dieser Aufgabe benötigt, die vertieft und flexibel zur Anwendung gebracht werden. Grundvoraussetzung zur Bearbeitung dieser Aufgabe ist die Kenntnis über den Winkelsummensatz im Dreieck. Außerdem wird das Verständnis über die Konstruktion und die Eigenschaften von rechtwinkligen und gleichschenkligen Dreiecken und über die Winkelhalbierende gefordert. Die Eigenschaften eines Kreises, insbesondere des Kreisradius und des Kreisbogens werden problemorientiert wiederholt. Zum Teil müssen diese Eigenschaften in der Zeichnung erkannt werden. Auch diese Variante trainiert die Problemlösefähigkeit der Schüler (geometrische Objekte „ansehen“ und Eigenschaften von Figuren ausnutzen). Die Schüler erhalten in diesem Zusammenhang eine tiefere Einsicht in geometrische Zusammenhänge, da diese für das Lösen ihres Problems erkannt und anschließend benutzt werden können. Bei dieser Lösungsvariante ergeben sich allerdings auch einige Schwierigkeiten für die Schüler. Die wohl größte Schwierigkeit besteht darin, dass die Schüler das gleichschenklige Dreieck ABC direkt am Anfang nicht erkennen und entsprechend die aufgeführte Argumentation nicht führen können. Darüber hinaus müssen grundlegende Eigenschaften geometrischer Objekte bekannt sein. Fehlen diese, ist ein erfolgreiches Lösen dieser Aufgabe im Gegensatz zur zeichnerischen Variante nicht möglich.


Im Kerncurriculum für das Gymnasium, Jahrgänge 5–10 findet man auf S. 29 bezüglich der Erwartungen zum inhaltsbezogenen Kompetenzbereich Größen und Messen am Ende von Schuljahrgang 6 die folgenden beiden Äußerungen: Die Schülerinnen und Schüler

"schätzen, messen und zeichnen Winkel" und "berechnen Winkelgrößen mit Hilfe von Neben-, Scheitel- und Stufenwinkelsatz und dem Winkelsummensatz für Dreiecke".

Da die Lösungsmöglichkeiten der Aufgabe verdeutlichen, dass die Aufgabe sowohl zeichnerisch durch die Konstruktion der Figur und das Ausmessen des gesuchten Winkels als auch rechnerisch durch die Verwendung des Winkelsummensatzes für Dreiecke und das Wissen über die Beziehungen verschiedener Winkel zueinander gelöst werden kann, beschreiben die beiden aus dem Kerncurriculum zitierten Erwartungen an Schülerinnen und Schüler am Ende einer 6. Klasse die in dieser Aufgabe geforderten Teilkompetenzen aus dem Kompetenzbereich Größen und Messen. Zur Abgrenzung der Erwartungen in diesem Kompetenzbereich an Schülerinnen und Schüler höherer Klassenstufen sei bemerkt, dass Schülerinnen und Schüler am Ende von Schuljahrgang 8 Winkelgrößen mit Hilfe des Thalessatzes und am Ende von Schuljahrgang 10 mit Hilfe von Ähnlichkeitsbeziehungen und trigonometrischen Beziehungen berechnen können sollen (vgl. S. 29). Da diese Hilfsmittel zur Lösung der Aufgabe nicht erforderlich sind, kann gefolgert werden, dass die Aufgabe in Klasse 5 oder Klasse 6 unterrichtet werden kann.

Anzumerken bleibt, dass das Wissen über die Bedeutung einer Winkelhalbierenden im Kerncurriculum erst am Ende von Klasse 8 festgeschrieben steht (vgl. S. 32), was obiger Einordnung zu widersprechen scheint. Dennoch ist es möglich, dass auch Schüler einer 5. oder 6. Klasse nach einer Erklärung den Begriff bereits adäquat verwenden können, sodass das Auftreten einer Winkelhalbierenden demnach keinen Grund darstellen soll, die Aufgabe für eine höhere Klassenstufe anzusetzen.


Versuch man die betrachtete Aufgabe einer Kompetenzstufe nach Blum, Roppelt und Müller zuzuordnen, so sollte dieser der Kompetenzstufe II zugesprochen werden. Die rechnerische Lösung dieser Aufgabe hat gezeigt, dass es an mehreren Stellen nötig ist, "bei zwei gegebenen Winkeln im Dreieck den dritten bestimmen" (Blum S.69), was der Kompetenzstufe Ib angehört und dem Mindeststandard für den Hauptschulabschluss entspricht. Zusätzlich sind zur Lösung der Aufgabe aber auch weitere Kompetenzen erforderlich, die der Kompetenzstufe II zugerechnet werden müssen. Dazu gehören die Fähigkeiten, "einfache geometrische Konstruktionen durchzuführen (wie das Zeichnen von Dreieck) und Winkelgrößen in solchen Figuren zu bestimmen" (S. 66) und "Winkelgrößen in Dreiecken unter Verwendung von Winkelsätzen zu bestimmen" (S. 69). Diese Kompetenzen entsprechen nach Blum, Roppelt und Müller dem Mindeststandard für den mittleren Schulabschluss und dem Regelstandard für den Hauptschulabschluss. Wenn man die untersuchte Aufgabe folglich aus gymnasialer Perspektive einordnen soll, so ist sie dem Mindeststandard zuzurechnen.


Heuristische Hilfsmittel: 
  • Das Einführen zweckmäßiger Bezeichnungen ist vor allem bei einer rechnerischen Lösung der Aufgabe sinnvoll. So sollten sinnvollerweise einige Punkte, Seiten und Winkel benannt werden, um sich konkret auf verschiedene Dreiecke in der Figur, vor allem aber auf gewisse zur Hilfe berechneten Winkel zu beziehen. Dieses Hilfsmittel wurde auch erkennbar in dem vorliegenden Lösungsvorschlag umgesetzt.
  • Zudem ist es gerade bei einer geometrischen Denkaufgabe unerlässlich, informativen Figuren zu verwenden, da Informationen aus der vorgegebenen geometrischen Denkfigur entnommen und weiter verarbeitet werden müssen.
  • Informativen Figuren inkl. Gleichungen wurden in dem Lösungsvorschlag vor allem im Rahmen der rechnerischen Lösungsmöglichkeiten genutzt, um zu verdeutlichen, welche Winkelgrößen bereits bekannt sind, und um davon ausgehend neue zu erschließen.
Heuristische Strategien: 
  • Sowohl ein Vorwärtsarbeiten als auch ein Rückwärtsarbeiten als auch eine Kombination aus beidem erscheinen bei dieser Aufgabe möglich. Gerade bei der rechnerischen Lösung kann es sinnvoll sein, sich rückwärts zu überlegen, welche Größen man bräuchte, um die Größe des Winkels \(\varepsilon\) zu berechnen, welche Größen man wiederum bräuchte, um diese Hilfsgröÿen zu ermitteln usw. bis man auf bereits gegebene Größen zurückgreifen und die Rechnungen dann vorwärts ausführen kann.
  • Je nachdem, zu welchem Zeitpunkt einer Unterrichtseinheit die Aufgabe konkret eingesetzt wird, können auch Analogieschlüsse bezogen auf früher gelöste Aufgaben sinnvolle Hilfen darstellen.
Heuristische Prinzipien: 
  • Das Nutzen der bereits eingezeichneten Zerlegung des Dreiecks in kleinere Dreiecke ist bei der Aufgabe zwingend erforderlich.

Da dieser Aufgabe zwischen 2 und 3 Punkten vergeben wurden, wurde diese Aufgabe mit * bzw. ** gekennzeichnet. Hier die Analyse:

Sprachlogische Komplexität: 

Die vorliegende Aufgabe ist eine sogenannte geometrische Denkaufgabe, der eine geometrische Konstruktion zugrunde liegt. Die Erklärung "w ist Winkelhalbierende" ist ein einfacher, verkürzter Hauptsatz, zum Verständnis des Ausdrucks "\(\alpha=?\)" sind keine sprachlichen Kompetenzen gefordert. Da keine explizite Aufgabenstellung vorgegeben ist, sondern die Aufgabe lediglich durch die formelhaft ausgedrückte Aufforderung zur Ermittlung der Winkelgröße \(\alpha\) gestellt wird, wird dieser Aufgabe die Stufe 0 hinsichtlich ihrer sprachlogischen Komplexität zugeordnet.

Kognitive Komplexität: 

Zur Lösung der Aufgabe muss die Auswahl der Denkvorgänge der Durchführung einzelner Schritte vorausgehen, da zu überlegen ist, in welcher Reihenfolge die Konstruktionsschritte vorgenommen (zeichnerische Lösung) oder welche Größen zunächst ermittelt werden müssen (rechnerische Lösung), um die Winkelgröße \(\alpha\) messen oder berechnen zu können. Dazu sind mitunter heuristische und strategische Überlegungen notwendig. Aus diesem Grund wird die vorliegende Aufgabe der Stufe 2 bezüglich ihrer kognitiven Komplexität zugeordnet.

Formalisierung von Wissen: 

Für die Lösung muss lediglich der Ausdruck "\(\alpha=?\)" richtig verstanden werden, wobei \(\varepsilon\) eine gängige Bezeichnung für einen Winkel oder seine Größe darstellt, sodass die Aufgabe der Stufe 0 zugeordnet werden kann. Eine Vergabe der Stufe 1 wäre an dieser Stelle zu hoch gegrien, da diese bei einfachen formalen Darstellungen wie z. B. bei Funktionstermen vergeben wird, die als deutlich komplexer als der Ausdruck "\(\alpha=?\)" einzustufen sind.

Formelhandhabung: 

Für eine zeichnerische Lösung der Aufgabe sind keinerlei algebraische Operationen erforderlich, sodass die Aufgabe unter diesem Gesichtspunkt der Stufe 0 zugeordnet werden muss.
Für eine rechnerische Lösung der Aufgabe müssen die Subtraktion sowie die Division durch 2 beherrscht werden, was mindestens der Stufe 1 hinsichtlich des Aspektes der Formelhandhabung entspricht. Allerdings sind die durchzuführenden Rechnungen naheliegend und weisen nicht viele Schritte auf, sodass eine Vergabe der Stufe 2 zu hoch gegrien wäre. Folglich wird für diese Aufgabe bezüglich der Formelhandhabung aus der Perspektive einer rechnerischen Lösung die Stufe 1 vergeben.

Stufenzuordnung: 
Formalisierung von Wissen
Stufe 0
Formelhandhabung
Stufe 0
Stufe 1
Kognitive Komplexität
Stufe 2
Sprachlogische Komplexität
Stufe 0

Hilfestellungen: 

Für den Fall, dass Schüler nicht wissen, wie sie ansetzen sollen, um die vorliegende Aufgabe zu lösen, könnten die folgenden Hilfestellungen hilfreich sein:

Allgemein-strategische Hilfen Inhaltlich-strategische Hilfen Inhaltliche Hilfen
Was ist in der Aufgabe gegeben? Diese Aufgabe ist sowohl zeichnerisch als auch rechnerisch lösbar. Welche dieser Lösungsmöglichkeiten erscheint dir am besten für dich geeignet? Wende ausgehend von den gegebenen Winkelgrößen Winkelsätze zur Berechnung fehlender Winkelgrößen an, bis du schließlich die gesuchte Winkelgröße angeben kannst.
Was ist in der Aufgabe gesucht? Wähle einen rechnerischen Lösungsweg. Überlege dir konkret, welche Winkelgrößen du wissen musst, um die gesuchte Winkelgröße zu berechnen. Überlege dann, welche von diesen du mit den gegebenen Winkelgrößen zuerst berechnen kannst.  
Sozialformen: 

Einzelarbeit mit anschließender Besprechung der Aufgabe im Plenum, Partnerarbeit mit anschließender Besprechung im Plenum oder die "Ich-Du-Wir-Methode" sind denkbar. Da Schüler sich selbst in die Aufgabe hineindenken müssen, um diese eigenständig zu lösen, ist eine Gruppenarbeit weniger sinnvoll, da sich dort einzelne (vor allem leistungsschwächere) Schüler von der Aufgabe ausnehmen können, wenn nur die leistungsstarken Schüler Lösungsideen äußern. Eine Besprechung der Aufgabe im Plenum erscheint wegen der niedrigen Jahrgangsstufe angemessen.

Differenzierungsmöglichkeiten: 
Hinweise für die Leistungsschwächeren Schülerinnen und Schüler
  • Um leistungsschwächeren Schülern die Aufgabe zu vereinfachen, könnten mehrere zur Lösung nützliche Winkel bereits markiert werden, damit diese Schüler sich einfacher durch die Aufgabe hangeln können. Alternativ könnte man Hinweise anfertigen, die schwächere Schüler bei Bedarf benutzen können, auf denen Hilfestellungen schriftlich oder anhand einer informativen Figur gegeben werden.
Hinweise für die Leistungsstärkeren Schülerinnen und Schüler
  • Man könnte leistungsstarke Schüler, die eine zeichnerische bzw. rechnerische Lösung gefunden haben, nach einer rechnerischen bzw. zeichnerischen Lösung suchen lassen, während im Allgemeinen von den Schülern nur eine mögliche Lösung erwartet wird.

Die Aufgabe scheint am sinnvollsten in einer produktiven Übungsphase einsetzbar, da für eine zeichnerische Lösung bereits erworbenes Wissen über die Konstruktion von Dreiecken und Kreisen und für eine rechnerische Lösung der Aufgabe verschiedene bekannte Winkelsätze vermischt angewendet werden sollen.



Bearbeitet von: Ana Kuzle & Sandra Pölking
nach oben
1078 Nutzer/-innen haben abgestimmt.

Feedback

Wir freuen uns auf Ihre Anregungen und konstruktive Rückmeldung zum Material.