-
Email : info(at)proffi-m.de
Geometrische Denkaufgabe: Winkeldetektiv 4
| Klasse | Schulstufe | Thema | Themengebiet | Schwierigkeit |
|---|---|---|---|---|
| 6/ 7/ 8 | Primarstufe, Sekundarstufe I | Winkelsätze (am Dreieck) | Größen und Messen, Raum und Form | *, ** |
| Heuristsche Hilfsmittel | Heuristische Prinzipien | Heuristische Strategien |
|---|---|---|
| Informative Figur, Gleichungen | Zerlegungs- und Ergänzungsprinzip, Invarianzprinzip | Vorwärtsarbeiten, Rückwärtsarbeiten, Kombiniertes Vorwärts- und Rückwärtsarbeiten, Systematisches Probieren, Analogieschlüsse |
Aufgabenstellung
|
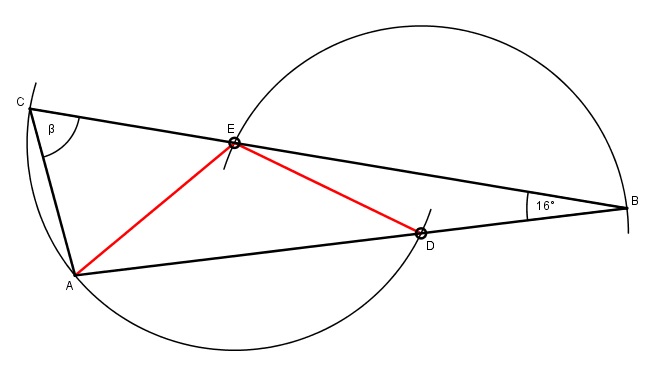
Wie groß ist der Winkel \(\beta \)? |
Quellenangabe:
Original aus Gebel, I., & Kuzle, A. (2016). Geo-Tricks: Ein Problemlösetraining in der Geometrie. MatheWelt, 196, 1–16.
Lösungsvariante 1 - Zeichnerische Lösung 1
Die Figur wird mit selbst gewählten Größen nachgezeichnet, sodass der Winkel \(\beta \) mit dem Geodreieck abgemessen werden kann.
|
1. In der Abbildung aus der Aufgabenstellung ist zu erkennen, dass das Dreieck \(\triangle ADE\) gleichschenklig ist, da die beiden Kreisbögen den gleichen Radius der Strecke \(\overline { DE } \) haben. Zeichne also zunächst ein beliebiges stumpfwinkliges gleichschenkliges Dreieck. Wähle für die Basis \(\overline { AD } =4cm\) und für die beiden Schenkel \(\overline { EA } =\overline { DE } =2,5cm\). Konstruiere nun das entsprechende Dreieck; zeichne dazu zuerst die Basis und im nächsten Schritt mit einem Zirkel Kreisbögen um die Mittelpunkte \(A\) und \(D\) mit einem Radius von jeweils \(2,5cm\). Der Schnittpunkt der beiden Kreisbögen bildet den Punkt \(E\). Verbinde diesen mit den Punkten \(A\) und \(D\) .
|
 |
|
|
2. Der Kreisbogen um \(D\) hat den Radius \(\overline { DE } =2,5cm\). Somit hat auch die Strecke \(\overline { DB } \) diese Länge, da \(B\) auf dem Kreisbogen liegt. Verlängere die Strecke \(\overline { AD } \) also entlang ihrer Ausrichtung um \(2,5cm\) nach rechts. Der Endpunkt der neuen Strecke bildet den Punkt \(B\).
|
 |
|
|
3. Zeichne eine Strecke ausgehend vom Punkt \(B\) im \(16°-Winkel\) zur Strecke \(\overline { AB } \) (in mathematisch negativem Drehsinn) zum Punkt \(E\).
|
 |
|
|
4. Der Kreisbogen um \(E\) hat den Radius \(\overline { EA } = \overline {DE} =2,5cm\), somit hat auch die Strecke \(\overline {EC}\) diese Länge, da \(C\) auf dem Kreisbogen liegt. Verlängere nun also die Strecke \(\overline { BE } \) um \(2,5cm\) nach links entlang ihrer Ausrichtung. Dort liegt der Punkt \(C\).
|
 |
|
|
5. Verbinde den Punkt \(C\) mit dem Punkt \(A\). Das vollständige Dreieck aus der Aufgabenstellung ist damit gezeichnet.
|
 |
|
|
6. Messe nun den Winkel \(\sphericalangle ACE=\beta \) mit dem Geodreieck ab. Dieser ist \(66°\) groß.
|
 |
Lösungsvariante 2 - Zeichnerische Lösung 2
Die Figur wird mit selbst gewählten Größen nachgezeichnet, sodass der Winkel ß mit dem Geodreieck abgemessen werden kann.
|
1. Zeichne den Punkt \(B\) und ausgehend von diesem zwei Strahlen, die einen \(16°-Winkel\) umschließen.
|
 |
|
|
2. In der Abbildung der Aufgabenstellung ist zu erkennen, das die beiden Kreisbögen den gleichen Radius \(\overline { ED } \) haben. Lege \(\overline { ED } =3cm\) fest. \(B\) liegt auf dem Kreisbogen um \(D\) und somit gilt \(\overline { ED } =\overline {DB}=3cm\). Trage daher den Punkt \(D\) auf \(Strahl 1\) in einem Abstand von \(3cm\) vom Punkt \(B\) ab.
|
 |
|
|
3. Zeichne mit einem Zirkel den Kreisbogen um den Mittelpunkt \(D\) durch den Punkt \(B\). Der Schnittpunkt dieses Kreisbogens mit \(Strahl 2\) bildet nun \(E\).
|
 |
|
|
4. Ziehe mit den gleichen Zirkeleinstellungen (da die beiden Kreisbögen den gleichen Radius \(\overline {ED}\) haben) einen weiteren Kreisbogen mit einem Radius von \(3cm\) um den Mittelpunkt \(E\) und durch die Punkte \(D\) und \(A\). Der Schnittpunkt dieses Kreisbogens mit \(Strahl 2\) bildet den Punkt \(C\).
|
 |
|
|
5. Verbinde die Punkte \(C\) und \(A\).
|
 |
|
|
6. Messe den Winkel \(\sphericalangle ACE=\beta \) mit dem Geodreieck ab. Es ergibt sich für \(\beta\) eine Größe von \(66°\).
|
 |
Lösungsvariante 3 - Rechnerische Lösung 1
gegeben:
gesucht: \(\beta\)
Lösung:
|
1.
|
Das Dreieck \(\triangle DBE\) ist gleichschenklig mit \(\overline {ED} = \overline {DB}\), da \(B\) und \(E\) auf demselben Kreis mit dem Mittelpunkt \(D\) liegen. Mit dem Basiswinkelsatz für gleichschenklige Dreiecke folgt: \(\alpha = \alpha' = 16°\) (1). Ebenso sind die Dreiecke \(\triangle AEC\) und \(\triangle ADE\) gleichschenklig, weil \(D\), \(A\), und \(C\) auf demselben Kreis mit dem Mittelpunkt \(E\) liegen und somit \(\overline {DE}= \overline {EA} = \overline {EC}\) gilt. Daher folgt wieder mit dem Basiswinkelsatz für gleichschenklige Dreiecke \(\beta =\beta'\) (2) und \(\varepsilon = \varepsilon'\) (3).
|
||||
|
2.
|
Weiterhin gilt nach dem Innenwinkelsummensatz für Dreiecke, dass die Summe der Innenwinkel eines beliebigen Dreiecks 180° beträgt. Somit gilt für die Dreiecke \(\triangle {DBE}\), \(\triangle {ADE}\) und \(\triangle {AEC}\) :
Mit (1), (2) und (3) folgt:
|
||||
|
3.
|
Um nun mit Gleichung (9) \(\beta\) berechnen zu können, muss noch \(\gamma\) ermittelt werden.
Mit dem Nebenwinkelsatz gilt: \(\gamma + (\sigma + \alpha') = 180°\) (10)
Ermittle \(\sigma\) mit Gleichung (8): \(2 \varepsilon + \sigma = 180°\) \(\Leftrightarrow \) \(\sigma = 180° - 2 \varepsilon\) (9)
Mit dem Nebenwinkelsatz gilt: \(\delta + \varepsilon = 180°\) (10) Durch Einsetzten von (7) in (10) ergibt sich: \(148° + \varepsilon = 180° \) \(\Leftrightarrow \) \(\varepsilon = 32°\) (11)
Durch Einsetzen von (11) in (9) folgt: \(\sigma = 180°-64°=116°\) (12)
Durch Einsetzen von (12) in (10) kann nun \(\gamma\) berechnet werden: \(\gamma + 116° + 16° = \gamma + 132° = 180°\) \(\Rightarrow\) \(\gamma = 48°\) (13) |
||||
|
4.
|
Nun lässt sich \(\beta\) durch Einsetzen von (13) in (9) ermitteln:
\(\beta =\frac { 180°-48° }{ 2 } =\frac { 132° }{ 2 } =66°\)
\(\beta\) beträgt somit \(66°\). |
Lösungsvariante 4 - Rechnerische Lösung 2
gegeben:
gesucht: \(\beta\)
Lösung:
|
1.
|
Mit dem Innenwinkelsummensatz für Dreiecke gilt für das Dreieck \(\triangle {ABC}\): \(\beta + (\beta' + \varepsilon') + \alpha = 180°\) (1) |
|||||||||||||||
|
2.
|
Die Dreiecke \(\triangle {AEC}\), \(\triangle {ADE}\) und \(\triangle {DBE}\) sind jeweils gleichschenklig, da \(C\), \(A\) und \(D\) auf einem Kreis mit dem Mittelpunkt \(E\) liegen und \(B\) und \(E\) auf einem Kreis mit dem Mittelpunkt \(D\). Somit gilt \(\overline {CE} = \overline {AE} = \overline {DE} = \overline {BD}\). Mit dem Basiswinkelsatz für gleichschenklige Dreiecke folgt also:
|
|||||||||||||||
|
3.
|
Durch Einsetzen von (2) und (3) in (1) ergibt sich:
|
|||||||||||||||
|
4.
|
Mit dem Nebenwinkelsatz gilt:
Durch Einsetzen von (6) in (5) folgt:
|
|||||||||||||||
|
5.
|
Mit dem Innenwinkelsummensatz für Dreiecke gilt für das Dreieck \(\triangle {DBE}\):
|
|||||||||||||||
|
Setze (4) in (8) ein:
|
||||||||||||||||
|
6.
|
Einsetzen von (9) in (7) ergibt:
Mit \(\alpha = 16°\) folgt:
\(\beta\) beträgt damit 66°. |
Die Winkeldetektivaufgabe eignet sich für den Einsatz in der sechsten Klasse, da sich die inhaltsbezogenen Kompetenzen der zeichnerischen Lösungen an den Standards der Niveaustufe D orientieren. Die rechnerischen Lösungen erfordern jedoch bei den Gleichungsumformungen auch Kompetenzen der Stufen E und F, weshalb auch ein Einsatz in der siebten und achten Klasse denkbar wäre.
Mit der geometrischen Denkaufgabe werden die inhaltsbezogenen Kompetenzbereiche [L2] Größen und Messen, [L3] Raum und Form und [L4] Gleichungen und Funktionen sowie die prozessbezogenen Kompetenzbereiche [K2] Probleme mathematisch lösen, [K4] Mathematische Darstellungen verwenden und [K6] Mathematisch kommunizieren aus dem brandenburgischen Rahmenlehrplan Mathematik für die Jahrgangsstufen 1-10 (LISUM (2015)), der ab dem Schuljahr 2017/18 gültig ist, gefördert.
Inhaltsbezogene Kompetenzformulierungen
Größen und Messen [L2]
Kompetenz 1: Die Schülerinnen und Schüler ermitteln die Größe eines gesuchten Winkels aus einer gegebenen Zeichnung, indem sie mit den in der Abbildung enthaltenen Winkelgrößen in Gradmaß rechnen.
"Die Schülerinnen und Schüler können Größen messen (auch [...] Winkelgrößen)" (LISUM (2015), Größenangaben bestimmen, Niveaustufe D, S.24), "Die Schülerinnen und Schüler können mit Größenangaben rechnen (auch mit [...] Winkelgrößen)" (LISUM (2015), Größen in Sachzusammenhängen berechnen, Niveaustufe D, S.25)
Erläuterung: Diese Kompetenz bezieht sich auf die beiden rechnerischen Lösungen. So beschriften die Lernenden bei diesen Lösungswegen zunächst die in der Abbildung enthaltenen Winkel und berechnen fehlende Winkelgrößen schrittweise mit dem Innenwinkelsummensatz für Dreiecke, mit dem Nebenwinkelsatz oder dem Basiswinkelsatz für gleichschenklige Dreiecke bis sie schließlich den gesuchten Winkel ermitteln können. Dabei rechnen sie mit dem Gradmaß.
Raum und Form [L3]
Kompetenz 2: Die Schülerinnen und Schüler erkennen gleichschenklige Dreiecke, indem sie Beziehungen zwischen geometrischen Objekten (hier zwischen Punkten, Strecken, Kreisbögen und Radien) beschreiben.
"Die Schülerinnen und Schüler können [...] geometrische Objekte qualitativ beschreiben" (LISUM (2015), Geometrische Objekte und ihre Eigenschaften beschreiben, Niveaustufe D, S.26), "Die Schülerinnen und Schüler können Beziehungen zwischen geometrischen Objekten (auch Winkel) beschreiben und zur Systematisierung nutzen" (LISUM (2015), Beziehungen zwischen geometrischen Objekten beschreiben, Niveaustufe D, S.26)
Erläuterung: Sowohl bei den zeichnerischen als auch bei den rechnerischen Lösungen erkennen die Kinder in der Abbildung, dass die Strecken , , und jeweils dem Radius der beiden Kreise entsprechen. Durch die Identifikation der Radien und der Folgerung aus dem identischen Radius der beiden Kreisbögen, dass , können in der Abbildung schließlich drei gleichschenklige Dreiecke identifiziert werden. Dafür ist es notwendig, dass die Schülerinnen und Schüler die Eigenschaften gleichschenkliger Dreiecke kennen.
Kompetenz 3: Die Schülerinnen und Schüler beschreiben Zusammenhänge zwischen Winkeln mit den entsprechenden Winkelsätzen (hier dem Innenwinkelsummensatz für Dreiecke, dem Basiswinkelsatz für gleichschenklige Dreiecke und dem Nebenwinkelsatz).
"Die Schülerinnen und Schüler können Beziehungen zwischen geometrischen Objekten beschreiben (auch Sätze über Dreiecke)" (LISUM (2015), Beziehungen zwischen geometrischen Objekten beschreiben, Niveaustufe E, S.26)
Erläuterung: Die Lernenden können die Winkelsätze (für Dreiecke) anwenden, um Zusammenhänge zwischen Winkeln zu beschreiben und letztendlich den gesuchten Winkel zu ermitteln.
Gleichungen und Funktionen [L4]
Kompetenz 4: Die Schülerinnen und Schüler lösen Gleichungen nach einer Variablen auf.
"Die Schülerinnen und Schüler können lineare Gleichungen und Verhältnisgleichungen lösen (auch mit Äquivalenzumformungen)" (LISUM (2015), Gleichungen und Gleichungssysteme lösen, Niveaustufe E, S.28), "Die Schülerinnen und Schüler können Gleichungen und lineare Gleichungssysteme lösen" (LISUM (2015), Gleichungen und Gleichungssysteme lösen, Niveaustufe F, S.28)
Erläuterung: Diese Kompetenz wird durch die beiden rechnerischen Lösungen gefördert, bei denen die Lernenden durch Anwenden der Winkelsätze Gleichungen aufstellen und diese lösen.
Prozessbezogene Kompetenzformulierungen
Probleme mathematisch lösen [K2]
Kompetenz 5: Die Schülerinnen und Schüler lösen eine Aufgabe unter Verwendung der heuristischen Strategien des Vorwärtsarbeitens, Rückwärtsarbeitens und des kombinierten Vorwärts- und Rückwärtsarbeitens sowie mithilfe von heuristischen Hilfsmitteln wie der Informativen Figur und der Gleichung.
"Die Schülerinnen und Schüler können Lösungsstrategien [...] entwickeln und nutzen" (LISUM (2015), S.19), "Die Schülerinnen und Schüler können heuristische Hilfsmittel zum Problemlösen anwenden" (LISUM (2015), S.19)
Erläuterung: Bei den beiden zeichnerischen Lösungen wird die gegebene Skizze betrachtet und nach Informationen gesucht, die für die Konstruktion notwendig sind. Durch das Nachzeichnen der Figur und schließlich das Abmessen des Winkels wird vorwärts gearbeitet. Es wird dabei eine informative Figur erstellt. Bei den rechnerischen Lösungswegen wird jeweils kombiniert vorwärts und rückwärts gearbeitet. Hier wird die Figur unter dem Gesichtspunkt des gesuchten Winkels betrachtet und darunter, wie das Gesuchte mithilfe des Gegebenen ermittelt werden kann. Es werden Zusammenhänge erkannt und einzelne Winkel mithilfe der entsprechenden Winkelsätze ermittelt. Diese Winkel stellen Teilziele dar, zu denen hin jeweils vorwärts gearbeitet wird. Dabei werden die Winkelsätze in Form von Gleichungen angewendet.
Mathematische Darstellungen verwenden [K4]
Kompetenz 6: Die Schülerinnen und Schüler dokumentieren die Winkelsätze in Form von Gleichungen.
"Die Schülerinnen und Schüler können [...] Gleichungen [...] zur Beschreibung von Sachverhalten nutzen" (LISUM (2015), S.20)
Erläuterung: Bei den rechnerischen Lösungswegen wenden die Lernenden den Basiswinkelsatz für gleichschenklige Dreiecke, den Innenwinkelsummensatz für Dreiecke sowie den Nebenwinkelsatz an, um einzelne Winkel zu ermitteln.
Mathematisch kommunizieren [K6]
Kompetenz 7: Die Schülerinnen und Schüler dokumentieren den Lösungsweg einer Aufgabe nachvollziehbar.
"Die Schülerinnen und Schüler eigene Problembearbeitungen und Einsichten dokumentieren und darstellen" (LISUM (2015), S.21)
Erläuterung: selbsterklärend
Heuristische Hilfsmittel:
Beim Lösen der Aufgabe ist zunächst als heuristisches Hilfsmittel das Erstellen einer informativen Figur bzw. die erneute Konstruktion der geometrischen Figur hilfreich. Dabei werden den SuS auf handelnde Weise die Zusammenhänge zwischen den verschiedenen Winkelgrößen bewusst. Durch das Zeichnen der Kreise wird deutlich, dass es sich bei den Dreiecken , und jeweils um gleichschenklige Dreiecke handeln muss. Auch die Aufstellung der entsprechenden Gleichungen anhand der verschiedenen Winkelsätze als weiteres heuristisches Hilfsmittel haben dem Lösungsfindungsprozess Struktur und Übersichtlichkeit geschenkt.
Heuristische Strategien:
Bei den beiden zeichnerischen Lösungen wird das Gegebene betrachtet und überlegt, wie die Figur damit konstruiert werden kann, sodass der Winkel schließlich abgemessen werden kann. Es handelt sich demnach um Vorwärtsarbeiten.
Für die beiden dargestellten Lösungswege werden verschiedene Heuristische Strategien verwendet. Während die erste rechnerische Lösungsweg zunächst mit Vorwärtsarbeiten angegangen wird und dann ein testendes kombiniertes Vorwärts- und Rückwärtsarbeiten zum Ziel führt, wird beim zweiten Lösungsweg ein stringentes Rückwärtsarbeiten angewendet. Für die erste rechnerische Lösung wird außerdem ein Analogieschluss als wesentliches Element der Lösungsfindung angewandt. Anhand des bekannten Nebenwinkelsatzes wird ermittelt, dass ist. Dieser Satz wird analog für drei sich schneidende Geraden verwendet, indem erkannt wird, dass zwei Winkel zu einem zusammengefasst werden können und dieser als Nebenwinkel zu angesehen werden kann, sodass folgender Zusammenhang ermittelt wird: . Der zweite rechnerische Lösungsweg ist noch mehr von der Aufstellung von Gleichungen geprägt, anhand derer stringent rückwärts in dem Innenwinkelsatz Schritt für Schritt die gesuchte Größe auf die gegebene Größe zurückgeführt wird. Während die erste rechnerische Lösung durch ein testendes Probieren und zusammenschreiben der aufgefallenen Zusammenhänge geprägt ist, kennzeichnet den zweiten rechnerischen Lösungsweg ein streng systematisches Vorgehen.
Heuristische Prinzipien:
Für alle Lösungen spielt das Zerlegungsprinzip eine Rolle, so wird das gegebene Dreieck in gleichschenklige Dreiecke unterteilt. Außerdem ist insbesondere bei den zeichnerischen Lösungen das Invarianzprinzip von Bedeutung, da die SuS erkennen müssen, dass die beiden in der Figur gegebenen Kreisbögen den gleichen Radius haben.
Die Winkeldetektivaufgabe hat nach Cohors-Fresenborg et al. bezüglich der zeichnerischen Lösungsvarianten einen Schwierigkeitsgrad von * und bezüglich der rechnerischen Lösungswege von **.
Sprachlogische Komplexität:
Die Sprachlogische Komplexität der Winkeldetektivaufgabe entspricht der Stufe 1, da es sich bei der Aufgabenstellung um einen einfachen Hauptsatz handelt, der allerdings keine Hinweise auf die Schritte bei der mathematischen Bearbeitung gibt.
Kognitive Komplexität:
Auch die Kognitive Komplexität lässt sich auf Stufe 1 ansiedeln, da Denkvorgänge parallel abzuarbeiten sind und Zusatzüberlegungen, wie beispielsweise die Gleichheit der Strecken , , und zu machen sind.
Formalisierung von Wissen:
Bezüglich der zeichnerischen Lösungswege entspricht die Formalisierung von Wissen der Stufe 0, da die Lösung lediglich grafisch und durch Abmessung erfolgt. Die rechnerischen Lösungswege lassen sich bezüglich der Formalisierung von Wissen dahingegen auf Stufe 1 ansiedeln, da sehr einfache Gleichungen aufzustellen sind.
Formelhandhabung:
Aus dem gleichen Grund wie bei der Formalisierung von Wissen lässt sich auch die Formelhandhabung bezüglich der zeichnerischen Lösungswege auf Stufe 0 einordnen. Die rechnerischen Lösungen lassen sich unter Berücksichtigung der Lerngruppe einer sechsten Klasse auf Stufe 2 ansiedeln, da eine höhere Anzahl algebraischer Schritte durchgeführt wird.
Stufenzuordnung:
Formalisierung von Wissen
Stufe 0
Stufe 1
Formelhandhabung
Stufe 0
Stufe 2
Kognitive Komplexität
Stufe 1
Sprachlogische Komplexität
Stufe 1
Hilfestellungen:
Bei der Bearbeitung der Winkeldetektivaufgabe durch die SuS können an einigen Stellen Probleme auftreten. Hier werden zwei solcher kritischer Stellen beschrieben und Möglichkeiten der Reaktion von Lehrpersonen dargestellt.
Eine erste Schwierigkeit könnte darin liegen, dass die SuS nicht auf die Idee kommen, das gegebene Dreieck in Teildreiecke zu unterteilen, um dann mithilfe der zuvor kennen gelernten Winkelsätze einzelne Winkel und letztendlich zu bestimmen. Tritt dieses Problem zu Beginn der Aufgabenlösung auf, so können die folgenden Hilfestellungen gegeben werden.
| Allgemein-strategische Hilfen | Inhaltsorientierte strategische Hilfen | Inhaltliche Hilfen |
| Was ist gegeben? Was ist gesucht? | Können dir bereits eingezeichnete Hilfslinien weiterhelfen? | Welche Winkel der gegebenen Figur kannst du bereits berechnen? |
| Wie gehen wir bei Problemlöseaufgaben mit einer gegebenen Figur vor? | Kannst du die Skizze um hilfreiche Objekte ergänzen? | Welche Winkelsätze kennst du? Wie lauten diese? |
| Wie gehen wir vor, wenn wir einen unbekannten Winkel in einer gegebenen Figur berechnen? | Kannst du bekannte Sätze über Winkel anwenden? | Suche gleichschenklige Dreiecke in der gegebenen Figur! |
Ein weiteres Problem, das insbesondere auch für die zeichnerische Lösung relevant ist, kann darin bestehen, dass die SuS nicht erkennen, dass die beiden Kreisbögen den gleichen Radius haben. In diesem Fall kann die Lehrperson den jeweiligen Schüler bzw. die jeweilige Schülerin mit folgenden Hinweisen auf eine "richtige Fährte" bringen.
| Allgemein-strategische Hilfen | Inhaltsorientierte strategische Hilfen | Inhaltliche Hilfen |
| Wie willst du bei der Aufgabe vorgehen? | Was weißt du über die eingezeichneten Hilfslinien? Warum? | Welche Strecken in der Planfigur kannst du zeichnen? |
| Was ist gegeben? | Welcher Zusammenhang besteht zwischen den eingezeichneten Hilfslinien und den Kreisbögen? | Welche Eigenschaften hat ein Kreis bzw. ein Kreisbogen? |
| Was weißt du über das Gegebene? | Gibt es Bestandteile der Figur, die in bestimmten Eigenschaften gleich sind? Welche und warum? | Was kannst du über die Strecken und sagen? |
Sozialformen:
- Einzelarbeit
- Partnerarbeit
Differenzierungsmöglichkeiten:
Die Winkeldetektivaufgabe lässt sich sowohl an leistungsschwächere als auch an leistungsstärkere Schülerinnen und Schüler anpassen.
Für leistungsschwächeren Schülerinnen und Schüler kann die Aufgabe wie folgt verändert werden:
- Es können mehrere Winkel und deren Maße vorgegeben werden (beispielsweise der Winkel ), sodass die Anzahl der zu berechnenden Winkel reduziert wird.
Für leistungsstärkere Schülerinnen und Schüler gibt es beispielsweise die folgenden Veränderungsmöglichkeiten:
- Die in der Aufgabenstellung gegebene Abbildung kann reduziert werden, indem nur noch das Dreieck , die Punkte und sowie die beiden und der vorgegeben sind, die beiden roten Strecken und jedoch nicht mehr enthalten sind. Dadurch wird es notwendig, dass sich die Lernenden selbstständig überlegen, warum die beiden Kreisbögen gleich groß sind, und sie müssen sich zusätzliche Hilfslinien einzeichnen.
- Alternativ könnte auch nur ein Kreisbogen, der durch die Punkte und , weggelassen werden und dafür nur angegeben werden, dass der Betrag der Strecken und gleich lang ist.
- Außerdem kann die Zusatzaufgabe gestellt werden, weitere unterschiedliche Lösungswege zu finden.
Da die Aufgabe komplex ist, eignet sie sich nicht zum Einstieg ins Thema "Winkelberechnungen".
Zum Produktiven Üben kann sie aber genutzt werden, um das Wissen über die unterschiedlichen Winkelsätze und Rechengesetze zu vertiefen und auch das Arbeiten mit Geodreieck und Zirkel zu üben. Den Schülerinnen und Schülern sollte genügend Zeit zur Bearbeitung der Aufgabe gegeben werden und vielleicht hilft es einigen Kindern auch, die Aufgabe in Partnerarbeit zu lösen. Bei der Besprechung der Lösung der Aufgabe sollten unterschiedliche Lösungswege beachtet werden.
Bearbeitet von: Simon Fromm, Nora Noltenius (ergänzt von Marisa Pfläging)
Feedback
Wir freuen uns auf Ihre Anregungen und konstruktive Rückmeldung zum Material.
Copyright © 2014-2017 - Ana Kuzle