-
Email : info(at)proffi-m.de
Geometrische Denkaufgabe: Winkeldetektiv 7
Fehlermeldung
Deprecated function: The each() function is deprecated. This message will be suppressed on further calls in FieldCollectionItemEntity->fetchHostDetails() (Zeile 313 von /www/htdocs/w0127817/beta.proffi-m.de/sites/all/modules/field_collection/field_collection.entity.inc).| Klasse | Schulstufe | Thema | Themengebiet | Schwierigkeit |
|---|---|---|---|---|
| 5/ 6/ 7 | Primarstufe, Sekundarstufe I | Winkelberechnungen | Größen und Messen, Raum und Form, Zahlen und Operationen | **, *** |
| Heuristsche Hilfsmittel | Heuristische Prinzipien | Heuristische Strategien |
|---|---|---|
| Informative Figur, Gleichungen | Zerlegungs- und Ergänzungsprinzip | Vorwärtsarbeiten, Kombiniertes Vorwärts- und Rückwärtsarbeiten, Systematisches Probieren |
Aufgabenstellung
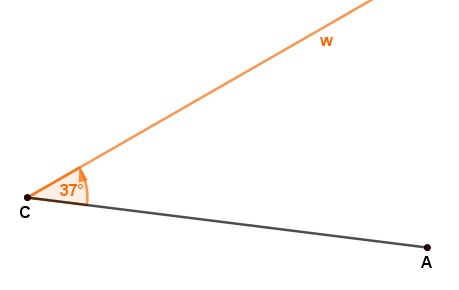
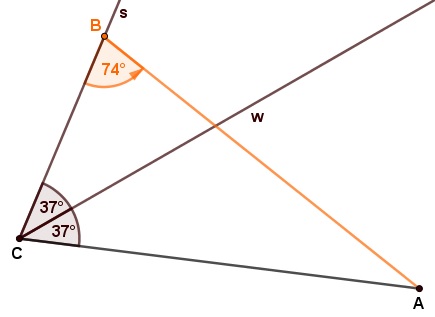
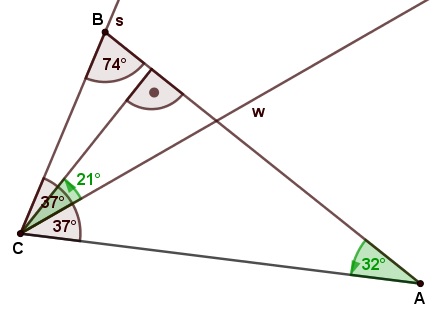
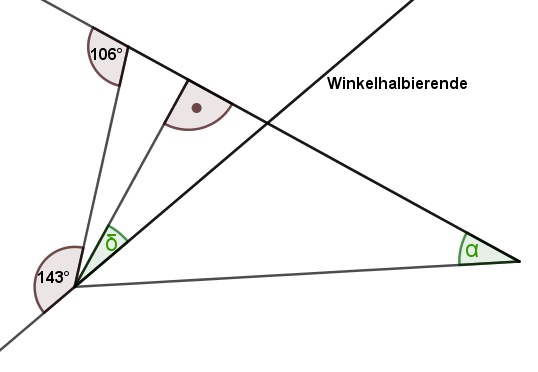
Gegeben ist die folgende Figur. Bestimme die Winkel α und δ. Dokumentiere deinen Lösungsweg in übersichtlicher und gut nachvollziehbarer Form (u.a. bezeichne deine Figur). Begründe deine Schritte!
Quellenangabe:
Gebel, I., & Kuzle, A. (2016). MatheWelt. mathematik lehren, 196, 1–16.
Für die rechnerischen Lösungswege werden die Winkel und Punkte der gegebenen Skizze zunächst beschriftet:
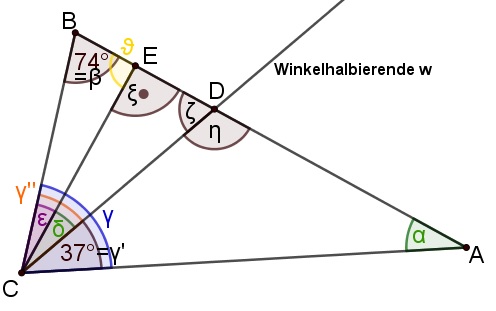
Bemerkung zu den Lösungen: Eine andere Notation der Winkel (z.B. \(\alpha =\sphericalangle BAC\)) wäre auch richtig, allerdings weniger gut nachvollziehbar. Deshalb werden die Lösungen hier mit den oben eingeführten Variablen dargestellt. Wird die andere Notation benutzt, so müssen lediglich die Punkte in der Skizze beschriftet werden.
Lösungsweg 1 - Rechnerische Lösung 1
1. Ermittle zunächst \(\alpha \):
|
Mit dem Innenwinkelsummensatz für Dreiecke gilt im Dreieck \(\triangle ABC\):
Um nun \(\alpha \) ermitteln zu können, muss \(\gamma \) berechnet werden. Da \(w\) die Winkelhalbierende des Winkels \(\gamma \) ist, gilt \(\gamma =2\cdot \gamma '=2\cdot 37°=74°\). Durch Einsetzen von \(\gamma =74°\) und \(\beta =74°\) in (*) folgt \(\alpha =32°\). |
2. Ermittle nun \(\delta \):
|
Für die Innenwinkelsumme im Dreieck \(\triangle AEC\) gilt mit dem Innenwinkelsummensatz für Dreiecke:
|
Lösungsweg 2 - Rechnerische Lösung 2
1. Ermittle zunächst \(\delta \):
|
Mit dem Innenwinkelsummensatz für Dreiecke gilt im Dreieck \(\triangle BCE\):
Da \(\vartheta \) der Nebenwinkel von \(\xi \) ist und \(\xi =90°\) gilt, folgt mit dem Nebenwinkelsatz \(\vartheta =90°\). Durch Einsetzen von \(\beta =74°\) und \(\vartheta =90°\) in (**) folgt \(\varepsilon =16°\).
Da \(w\) die Winkelhalbierende von \(\gamma \) ist und diese den Winkel \(\gamma \) in \(\gamma '\) und \(\gamma ''\) unterteilt, gilt:
|
2. Ermittle nun \(\alpha \):
|
Mit dem Innenwinkelsummensatz gilt im Dreieck \(\triangle DEC\):
Aufgrund des Nebenwinkelsatzes gilt:
Mit dem Innenwinkelsummensatz gilt im Dreieck \(\triangle ADC\):
|
Lösungsweg 3 - Rechnerische Lösung 3
1. Ermittle zunächst \(\delta \):
|
Mit dem Innenwinkelsummensatz für Dreiecke gilt im Dreieck \(\triangle CDE\):
Um \(\delta \) ermitteln zu können, muss nun erst einmal \(\zeta \) ermittelt werden. Da die Winkelhalbierende \(w\) den Winkel \(\gamma\) in \(\gamma '\) und \(\gamma ''\) unterteilt und \(\gamma ' = 37°\) gilt, gilt auch \(\gamma '' = 37°\). Auch im Dreieck \(\triangle BCD\) gilt der Innenwinkelsummensatz für Dreiecke:
Durch Einsetzen von \(\zeta =69°\) und \(\xi =90°\) in (***) ergibt sich \(\delta =21°\). |
2. Ermittlung von \(\alpha \):
|
Mit dem Nebenwinkelsummensatz gilt:
Mit dem Innenwinkelsummensatz für Dreiecke gilt im Dreieck \(\triangle ADC\):
|
Lösungsweg 4 - Zeichnerische Lösung
| 1. Zeichne eine beliebige Strecke mit den Endpunkten \(A\) und \(C\). |  |
|
2. Setze das Geodreieck in Punkt \(C\) an und zeichne einen Strahl \(w\) in einem Winkel von \(37°\) zur Strecke \(\overline { AC } \). So entsteht die Winkelhalbierende \(w\). |
|
|
3. Setze das Geodreieck erneut in Punkt \(C\) an und zeichne einen Strahl \(s\) in einem Winkel von \(37°\) zur Winkelhalbierenden \(w\). Da \(w\) den Winkel \(\sphericalangle ACB\) in der Hälfte teilt, muss auf dem gezeichneten Strahl \(s\) der Punkt \(B\) liegen. |
|
|
4. Es ist bekannt, dass \(\sphericalangle CBA=74°\). Lege also das Geodreieck am Strahl \(s\) an und messe ab, welche Stelle auf \(s\) sich mit dem Punkt \(A\) so verbinden lässt, dass gilt \(\sphericalangle CBA=74°\). Markiere diese Stelle als Punkt \(B\) und verbinde den Punkt \(A\) mit dem Punkt \(B\). |
|
| 5. Fälle das Lot vom Punkt \(C\) auf die Strecke \(\overline { AB } \). |
|
|
6. Durch Identifizieren von \(\alpha \) und \(\delta \) in der Skizze und durch Abmessen ergibt sich: \(\alpha =32°\) \(\delta =21°\) |
|
Die Winkeldetektivaufgabe lässt sich aufgrund der bei der Lösung geforderten Kompetenzen auf Niveaustufe D des brandenburgischen Rahmenlehrplans (vgl. Geförderte Kompetenzen) frühestens in der fünften Jahrgangsstufe, eher aber in der sechsten Jahrgangsstufe im Rahmen der Unterrichtsthematik "Winkelsätze" einsetzen. Laut LISUM (2015, S.54) sollen die Schülerinnen und Schüler im Laufe der fünften und sechsten Klasse auf Niveaustufe D "Lösungen von Gleichungen [...] mit einer Rechenoperation und einem Platzhalter" begründen können. Dies stellt eine notwendige Voraussetzung für die rechnerischen Lösungen dar, weshalb es sinnvoll ist, die Aufgabe erst nach der Thematisierung von Gleichungen mit Platzhaltern einzusetzen. Auch ein Einsatz in der siebten Jahrgangsstufe zur Wiederholung und Anknüpfung an bereits bekanntes Wissen über geometrische Objekte (Winkel, Winkelhalbierende, Dreiecke) zu Beginn der Unterrichtsthematik "Besondere Punkte und Linien im Dreieck" wäre daher denkbar.
Mit der geometrischen Denkaufgabe Winkeldetektiv 7 werden der inhaltsbezogene Kompetenzbereich [L2] Größen und Messen und [L3] Raum und Form sowie die prozessbezogenen Kompetenzbereiche [K1] Mathematisch argumentieren, [K2] Probleme mathematisch lösen, [K4] Mathematische Darstellungen verwenden und [K5] Mit symbolischen, formalen, technischen Elementen der Mathematik umgehen aus dem brandenburgischen Rahmenlehrplan (Teil C) Mathematik für die Jahrgangsstufen 1-10 (LISUM, 2015), der ab dem Schuljahr 2017/18 gültig ist, gefördert.
Inhaltsbezogene Kompetenzformulierungen
Größen und Messen [L2]
Kompetenz 1: Die Schülerinnen und Schüler berechnen gesuchte Winkelgrößen mithilfe gegebener Winkel und deren entsprechenden Größen und Einheiten.
"Die Schülerinnen und Schüler können die verschiedenen Größen und ihre Einheiten nutzen (auch [...] Winkelgrößen)" (LISUM, 2015, Vorstellungen zu Größen und ihren Einheiten nutzen, Niveaustufe D, S.24), "Die Schülerinnen und Schüler können Größen messen (auch [...] Winkelgrößen)" (ebd., Größenangaben bestimmen, Niveaustufe D, S.24), "Die Schülerinnen und Schüler können mit Größenangaben rechnen (auch mit [...] Winkelgrößen)" (ebd., Größen in Sachzusammenhängen berechnen, Niveaustufe D, S.25)
Erläuterung: Grundvoraussetzung für die Lösung der Aufgabe ist, dass die Lernenden eine Vorstellung von den geometrischen Objekten Winkeln haben, ihre Einheit kennen und mit Winkeln angemessen umgehen können, um mithilfe gegebener Größen gesuchte Winkel ermitteln zu können.
Raum und Form [L3]
Kompetenz 2: Die Schülerinnen und Schüler wenden Sätze über Beziehungen zwischen Winkeln (Innenwinkelsummensatz im Dreieck, Nebenwinkelsatz) an, um unbekannte Winkelgrößen zu ermitteln.
"Beschreiben von Winkelbeziehungen an geschnittenen Geraden bzw. Parallelen sowie in Dreiecken (Scheitelwinkel, Nebenwinkel, Stufenwinkel, Innenwinkel) und Nutzen für Argumentationen" (LISUM, 2015, Beziehungen zwischen geometrischen Objekten beschreiben, Niveaustufe D, S.48), "Die Schülerinnen und Schüler können Beziehungen zwischen geometrischen Objekten beschreiben (auch Sätze über Dreiecke) und Nutzen für Argumentationen" (LISUM, 2015, Beziehungen zwischen geometrischen Objekten beschreiben, Niveaustufe E, S.26)
Erläuterung: Die Schülerinnen und Schüler müssen bei der Lösung Zusammenhänge (Lage- und Größebeziehungen) zwischen den verschiedenen Winkeln erkennen, die Figur in Teilfiguren unterteilen und in diesen die entsprechenden Winkelsätze anwenden, um schrittweise unbekannte Winkel zu ermitteln und letztendlich zu den gesuchten Größen zu gelangen.
Kompetenz 3: Die Schülerinnen und Schüler kennen Eigenschaften geometrischer Objekte (wie dem rechten Winkel und der Winkelhalbierenden).
"Erkennen und Beschreiben der Eigenschaften von Winkeln und Dreiecken" (LISUM, 2015, Geometrische Objekte und ihre Eigenschaften beschreiben, Niveaustufe D, S.48), "Beschreiben besonderer Linien in Dreiecken und Körpern (z. B. Höhe, Seitenhalbierende, Mittelsenkrechte)" (ebd., Niveaustufe E)
Erläuterung: Für die Lösung der Aufgabe ist es notwendig, dass die Lernenden den gegebenen rechten Winkel \(\xi \) identifizieren und erkennen, dass die Winkelhalbierende \(w\) den Winkel \(\gamma \) halbiert und in die beiden Hälften \(\gamma '\) und \(\gamma ''\) unterteilt.
Prozessbezogene Kompetenzformulierungen
Mathematisch argumentieren [K1]
Kompetenz 4: Die Schülerinnen und Schüler begründen ihren Lösungsweg durch das Festhalten ihrer Argumente mittels mathematischer Fachsprache.
"Die Schülerinnen und Schüler können Begründungen [...] zunehmend selbstständig entwickeln" (LISUM, 2015, S.19) "Die Schülerinnen und Schüler können mehrschrittige Argumentationen zur Begründung und zum Beweisen mathematischer Aussagen entwickeln" (ebd.)
Erläuterung: Die Schülerinnen und Schüler müssen ihren Lösungsweg in nachvollziehbarer Form dokumentieren. Bei der Anwendung der Winkelsätze nennen sie die entsprechenden Winkelsätze und geometrischen Objekte mit korrekter Bezeichnung und benennen Winkel mithilfe mathematisch korrekter Notation.
Probleme mathematisch lösen [K2]
Kompetenz 5: Die Schülerinnen und Schüler wenden heuristische Strategien (wie das kombinierte Vorwärts- und Rückwärtsarbeiten sowie das Systematische Probieren) und heuristische Hilfsmittel (wie die Informative Figur und Gleichungen) an, um eine Aufgabe, zu der sie noch keine Lösungsroutine haben, zu bearbeiten.
"Die Schülerinnen und Schüler können Aufgaben bearbeiten, zu denen sie noch keine Routinestrategie haben (sich zu helfen wissen)" (LISUM, 2015, S.19), "Die Schülerinnen und Schüler können Lösungsstrategien (z. B. vom Probieren zum systematischen Probieren) entwickeln und nutzen heuristische Hilfsmittel zum Problemlösen anwenden" (ebd.)
Erläuterung: Das Anwenden von Heurismen ist für die Lösung der Winkeldetektivaufgabe hilfreich (siehe Heurismen).
Mathematische Darstellungen verwenden [K4]
Kompetenz 6: Die Schülerinnen und Schüler nutzen und ergänzen die vorgegebene Zeichnung, um den gesuchten Winkel zu ermitteln.
"Die Schülerinnen und Schüler können geeignete Darstellungen für das Bearbeiten mathematischer Sachverhalte und Probleme auswählen, nutzen und entwickeln" (LISUM, 2015, S.20), "Die Schülerinnen und Schüler können Darstellungen zielgerichtet verändern" (ebd.)
Erläuterung: Durch die gegebene Zeichnung erhalten die Lernenden wichtige Informationen, die sie für die Lösung entschlüsseln müssen. Darüber hinaus ist es für eine nachvollziehbare Dokumentation des Lösungsweges notwendig, die Zeichnung um Bezeichnungen für Punkte und Winkel zu ergänzen. Auch farbliche Markierungen können für die Übersichtlichkeit hilfreich sein.
Mit symbolischen, formalen, technischen Elementen der Mathematik umgehen [K5] (insbesondere bezüglich der rechnerischen Lösungswege)
Kompetenz 7: Die Schülerinnen und Schüler können mathematische Gleichungen nach einer gesuchten Variablen umformen.
"Die Schülerinnen und Schüler können mathematische Verfahren routiniert ausführen" (LISUM, 2015, S.20)
Erläuterung: Die Schülerinnen und Schüler müssen beispielsweise den Winkelsummensatz für Dreiecke sowie den Nebenwinkelsummensatz nach dem gesuchten Winkel durch entsprechende Operationen der Addition und Subtraktion umformen.
Heuristische Hilfsmittel:
- In der gegebenen Zeichnung können die verschiedenen Dreiecke sowie Winkel und ihre Beziehungen zueinander erkannt werden. Darüber hinaus sind wichtige Hinweise zur Lösung, wie die Winkelhalbierende, in der Skizze gegeben. Durch Beschriftung der Zeichnung können die zur Lösung notwendigen mathematischen Sätze formuliert werden. Somit handelt es sich bei der Abbildung um eine Informative Figur.
- Um die unbekannten Winkelgrößen zu ermitteln werden außerdem bei den rechnerischen Lösungen Gleichungen aufgestellt und nach der jeweiligen gesuchten Größe umgeformt.
Heuristische Strategien:
- Bei der zeichnerischen Lösung wird vom Gegebenen zum Gesuchten hin vorwärts gearbeitet: Die gegebene Zeichnung wird betrachtet und es wird überlegt, mit welchen Schritten sich die dargestellte Figur mit den gegebenen Winkelgrößen "peu à peu" konstruieren lässt. Letztendlich können die gesuchten Winkelgrößen in der so gezeichneten Figur mit dem Geodreieck abgemessen werden.
- Bei den rechnerischen Lösungswegen wird kombiniert vorwärts und rückwärts gearbeitet: Ausgehend von den gesuchten Winkeln wird die gegebene Zeichnung betrachtet und überlegt, welche Winkel zunächst ermittelt werden müssen (Teilziele), um letztendlich den gesuchten Winkel berechnen zu können. Es wird also sowohl vom Gesuchten als auch vom Gegebenen ausgehend das Gesuchte ermittelt.
- Bei den rechnerischen Lösungen wird darüber hinaus zunächst versucht, die in der Figur vorhandenen Dreiecke zu erkennen, dann ihre Winkel in Beziehung zu setzen und schließlich so viele Winkel wie möglich zu ermitteln. Es wird somit systematisch probiert, welche Winkel ermittelt werden können, um schließlich auf die gesuchten Winkelgrößen zu stoßen.
Heuristische Prinzipien:
- Die gegebene Figur lässt sich in verschiedene Dreiecke unterteilen, in denen zunächst Winkel berechnet werden können. Somit spielt das Zerlegungsprinzip bei der Lösung des Problems eine Rolle.
Die Winkeldetektivaufgabe hat nach Cohors-Fresenborg et al. bezüglich der zeichnerischen Lösung mit insgesamt 3 erreichten Punkten einen Schwierigkeitsgrad von ** und bezüglich der rechnerischen Lösungswege mit insgesamt 7 erreichten Punkten einen Schwierigkeitsgrad von ***.
Sprachlogische Komplexität:
Die Sprachlogische Komplexität der Winkeldetektivaufgabe lässt sich auf Stufe 1 ansiedeln, da es sich bei der Aufgabenstellung zwar um einfache Hauptsätze handelt, diese allerdings keine Hinweise auf die Reihenfolge der Schritte bei der mathematischen Bearbeitung geben.
Kognitive Komplexität:
Vor der Bearbeitung der Aufgabe müssen Überlegungen gemacht werden, wie, also mit welchen Heurismen die Aufgabe gelöst werden kann. Dabei muss die gegebene Zeichnung betrachtet werden und es muss genau analysiert werden, welche Bedingungen berücksichtigt werden müssen, bzw. welche Informationen gegeben sind. Somit lässt sich die Kognitive Komplexität in Anbetracht des Einsatzes der Aufgabe in einer fünften oder sechsten Klasse auf Stufe 2 anordnen.
Formalisierung von Wissen:
Die Formalisierung von Wissen entspricht bezüglich der zeichnerischen Lösung der Stufe 0, da die Lösung lediglich in graphischer Form erfolgt. Bezüglich der rechnerischen Lösungswege entspricht die Formalisierung von Wissen unter Berücksichtigung einer fünften oder sechsten Klasse hingegen der Stufe 2, da die Innenwinkelsumme in Dreiecken sowie der Nebenwinkelsummensatz mit Gleichungen oder Termen, die eigenständig von den Schülerinnen und Schülern erbracht werden, dargestellt werden.
Formelhandhabung:
Auch die Formelhandhabung lässt sich bezüglich der zeichnerischen Lösung auf Stufe 0 ansiedeln, da bei diesem Lösungsweg keine algebraischen Operationen erforderlich sind. Bezüglich der rechnerischen Lösung lässt sich die Formelhandhabung auf Stufe 2 ansiedeln, da die aufgestellten Gleichungen nach dem jeweiligen gesuchten Winkel umgeformt werden müssen und die Schülerinnen und Schüler einer fünften oder sechsten Klasse wahrscheinlich noch wenige Erfahrungen beim Umformen von Gleichungen haben.
Stufenzuordnung:
Formalisierung von Wissen
Stufe 0
Stufe 2
Formelhandhabung
Stufe 0
Stufe 2
Kognitive Komplexität
Stufe 2
Sprachlogische Komplexität
Stufe 1
Hilfestellungen:
Für Problemlöseaufgaben ist eine individuelle Barriere charakteristisch, die bei der Aufgabenlösung überwunden werden muss, um vom Anfangszustand zum Zielzustand zu gelangen. Kann diese Hürde von den Schülerinnen und Schülern nicht eigenständig überwunden werden, so sollten individuelle Hilfen gegeben werden, sodass sie für diese und weitere Aufgaben nicht frustriert und demotiviert werden.
Die Schülerinnen und Schüler könnten zunächst nicht auf die Idee kommen, die gegebene Skizze für die Aufgabenlösung zu nutzen und diese zu verändern, bzw. mit Bezeichnungen für Punkte und Winkel zu ergänzen, die zunächst ermittelt werden müssen, um schließlich die gesuchten Winkel berechnen zu können. Tritt diese anfängliche Schwierigkeit bezüglich der heuristischen Vorgehensweise bei der Lösung auf, so können die folgenden allgemein-strategischen, inhaltsorientierten strategischen und inhaltlichen Hilfen gegeben werden.
| allgemein-strategische Hilfen | inhaltsorientierte strategische Hilfen | inhaltliche Hilfen |
| Nutze die Skizze! | Kannst du mithilfe der Skizze erkennen, welche mathematischen Sätze du anwenden kannst, um die gesuchten Winkel zu bestimmen? | Welche Winkelsätze haben wir in den letzten Unterrichtsstunden behandelt? |
| Du kannst auch Winkel und Punkte in der Skizze mit selbst eingeführten Platzhaltern bezeichnen. | Kannst du die gesuchten Winkel direkt mit den gegebenen Größen ermitteln, oder musst du in mehreren Schritten vorgehen? | Was besagt der Nebenwinkelsatz und der Innenwinkelsummensatz für Dreiecke? |
| Was ist in der Aufgabenstellung gegeben? Arbeite mit dem Gegebenen! | Kannst du die Figur in Teilfiguren unterteilen? Welche Größen haben die Winkel in diesen Teilfiguren? | Kannst du den Innenwinkelsummensatz für Dreiecke anwenden? |
Außerdem könnten die Lernenden Schwierigkeiten damit haben, die Eigenschaften der in der Skizze gegebenen Objekte (des rechten Winkels, der Winkelhalbierenden und der Teildreiecke) bei der Lösung zu nutzen, um unbekannte Winkelgrößen zu ermitteln.
| allgemein-strategische Hilfen | inhaltsorientierte strategische Hilfen | inhaltliche Hilfen |
| Was ist in der Zeichnung gegeben? | Gibt es Geraden, oder Winkel in der Figur, die dir weiterhelfen können? | Welche geometrischen Objekte kannst du in der gegebenen Abbildung erkennen? |
| Betrachte die Abbildung genau! | Zerlege die gegebene Figur in einzelne Bestandteile! |
Welche Eigenschaft hat die Winkelhalbierende? |
| Markiere zusammenhängende Größen und/oder Objekte farblich! Markiere dir die gesuchten Größen in einer anderen Farbe! | Kannst du Kenntnisse über bestimmte geometrische Objekte anwenden? | Was gilt für die Winkelsumme im Dreieck? |
Sozialformen:
- Einzelarbeit
- Partnerarbeit
Differenzierungsmöglichkeiten:
Die Winkeldetektivaufgabe lässt sich sowohl für leistungsschwächere als auch für leistungsstärkere Schülerinnen und Schüler so anpassen, dass sie für die jeweiligen Lernenden eine angemessene Herausforderung darstellt.
Für leistungsschwächere Schülerinnen und Schüler kann die Aufgabe folgender Maßen abgewandelt werden:
- qualitative Differenzierung durch Verallgemeinern: Die gegebene Zeichnung kann um das Lot auf die Strecke \(\overline { AB } \) sowie den Winkel \(\delta \) reduziert werden, sodass die Schülerinnen und Schüler nur noch den Winkel \(\alpha \) berechnen müssen. In diesem Fall könnte folgende Aufgabenstellung gegeben werden:
Gegeben ist die folgende Figur. Bestimme den Winkel \(\alpha \). Dokumentiere deinen Lösungsweg in übersichtlicher und gut nachvollziehbarer Form (u.a. bezeichne deine Figur). Begründe deine Schritte!
Erläuterung: Durch diese Veränderung wird die Abbildung übersichtlicher und die notwendigen Schritte werden leichter ersichtlich. Im Prinzip fordert die Aufgabe nichtsdestotrotz die gleichen Kompetenzen und sie testet das gleiche Wissen (die Anwendung der Innenwinkelsumme in Dreiecken sowie die Eigenschaften der Winkelhalbierenden).
- quantitative Differenzierung durch Vorgabe eines zusätzlichen Winkels oder mehrerer zusätzlicher Winkel in der Figur
- Die Außenwinkel könnten zusätzlich angegeben werden, sodass diese für die Berechnung der fehlenden Innenwinkel in der Figur nur noch von 180° subtrahiert werden müssen.
- Es könnten die ersten Schritte für eine Lösung der Aufgabe angegeben werden, sodass die individuelle Barriere beim Problemlösen leichter überwunden werden kann.
- Bevor die Schülerinnen und Schüler die Aufgabe lösen sollen, könnten notwendige Begriffe und Zusammenhänge (wie die Winkelhalbierende, verschiedene Winkel im Allgemeinen, der Nebenwinkelsatz und die Innenwinkelsumme im Dreieck) mit ihnen noch einmal besprochen werden.
- Den Lernenden könnten Hilfe-/Tippkärtchen (Innenwinkelsatz im Dreieck, Was ist eine Winkelhalbierende?, etc.) zur Verfügung gestellt werden, die sie aufdecken können, falls sie an bestimmten Stellen im Lösungsprozess nicht weiterkommen.
Für leistungsstärkere Schülerinnen und Schüler kann die Aufgabe wie folgt verändert werden:
- qualitative Differenzierung durch Spezialisieren: Die gegebene Zeichnung kann um eine weitere parallel zu der Winkelhalbierenden verlaufende Gerade mit dem zusätzlich zu berechnenden Winkel \(\mu \) eingefügt werden. Es könnte folgende Aufgabenstellung gegeben werden:
Gegeben ist die folgende Figur. Bestimme die Winkel \(\alpha \), \(\delta \) und \(\mu \). Dokumentiere deinen Lösungsweg in übersichtlicher und gut nachvollziehbarer Form (u.a. bezeichne deine Figur). Begründe deine Schritte!
Erläuterung: Diese Aufgabe verlangt zusätzlich die Anwendung des Stufenwinkelsatzes und des Nebenwinkelsatzes (besondere Winkelpaare), oder die Anwendung von Kongruenzsätzen am Dreieck.
Mögliche weitere Differenzierung durch Ergänzung: Diese Aufgabe kann sogar noch erweitert werden, indem die Länge bestimmter Streckenabschnitte angegeben wird und die Schülerinnen und Schüler mithilfe der Strahlensätze andere Streckenabschnitte berechnen sollen.
- Die Angaben der Winkelgrößen können reduziert und dafür können andere Angaben gegeben werden, mit denen die Schülerinnen und Schüler dann die zur Lösung notwendigen Winkel ermitteln können. Beispielsweise könnten anstelle der gegebenen Winkel in der Figur die Außenwinkel gegeben sein, sodass die Innenwinkel erst noch ermittelt werden müssen:
Die Schülerinnen und Schüler benötigen für die Lösung der Winkeldetektivaufgabe Vorwissen über die Innenwinkelsumme im Dreieck, die Winkelhalbierende, den Nebenwinkelsatz und die Größe eines rechten Winkels, daher eignet sich die Aufgabe nicht zum Einstieg oder zur Erarbeitung dieser inhaltlichen Aspekte, sondern eher zum Produktiven Üben und zum forschenden entdeckenden Lernen. So können die Lernenden mit dieser Aufgabe das zuvor erlernte Wissen vertiefen und darüber hinaus verschiedene Lösungsansätze erkennen und neue Handlungskompetenzen durch die Lösung eines Problems, zu dem noch keine Lösungsroutine vorhanden ist, erwerben. Die Schülerinnen und Schüler können anhand der Aufgabe Heurismen zur Aufgabenlösung kennenlernen und es kann ein tieferes Verständnis für die bereits bekannten mathematischen Zusammenhänge erlangt werden.
Bearbeitet von: T. Bölsdorf, J. Colmsee, P. Cierpinski, A. Dizman, A. Ernstberger, L. Fritscher, B. Kaulisch, J. Keß, A. Liesegang, A. Lorenz, L. Podlipny, R. Rosenke, F. Tappert, A. Zwanziger, C. Schmidt (ergänzt von M. Pfläging)
Feedback
Wir freuen uns auf Ihre Anregungen und konstruktive Rückmeldung zum Material.
Copyright © 2014-2017 - Ana Kuzle