Origami-Aufgabe: Schachtel Falten

Fehlermeldung

Deprecated function: The each() function is deprecated. This message will be suppressed on further calls in FieldCollectionItemEntity->fetchHostDetails() (Zeile 313 von /www/htdocs/w0127817/beta.proffi-m.de/sites/all/modules/field_collection/field_collection.entity.inc).
Klasse Schulstufe Thema Themengebiet Schwierigkeit
8/ 9/ 10 Sekundarstufe I Größen mit Hilfe des Satz des Pythagoras bestimmen Funktionaler Zusammenhang, Größen und Messen, Raum und Form *, ***

Aufgabenstellung

Kann man eine allgemeine Formel für das Volumen der Box finden, wenn die Kantenlänge des quadratischen Blattes a ist (i.a.W. V=V(a))? Dokumentiere und begründe deine Lösung ausführlich!
 
                

 

 

Quellenangabe:

DE YOUNG, M. J.: Maths in the box. Mathematics Teaching in the Middle School.15 (3). 2009. S.134-141; (YouTube-Video: https://www.youtube.com/watch?v=TFtl4rd_Llw, 13.07.16, 20.00Uhr)


Lösungsvariante 1: Geometrische Lösung durch Entfalten und erneutes schrittweises Falten
 
Schritt 1: Falten der Schachtel
Mithilfe des anleitenden Videos wird aus dem quadratischen Blatt der Seitenlänge a eine Schachtel gefaltet.
Schritt 2: Volumenformel für die Schachtel
Das Volumen der Box lässt sich mit der Volumenformel für Quader berechnen:
\(V=a\cdot b\cdot c\quad \Rightarrow \quad V=b²\cdot c\)
 
 Skizze 1.1
Schritt 3: Markierung markanter Objekte
Die Kanten b, bzw. die Grundfläche und die Höhe c werden auf der Box markiert.
Dafür gibt es verschiedene Möglichkeiten:
  1. Markierung auf der Außenfläche
  2. Markierung auf der Innenfläche
  3. Markierungen auf der inneren und/oder äußeren Fläche
Schritt 4: Auseinanderfalten
Um einen Zusammenhang zwischen den Seitenlängen b und a bzw. c und a zu erkennen, wird das Blatt nun wieder auseinandergefaltet.
 
Wie auf den obigen Fotos zu erkennen ist, sind die Seiten c und b bei manchen Varianten der Markierung auf der Vorderseite und der Rückseite aufgezeichnet. Um auch in diesen Fällen einen Zusammenhang zu sehen, werden die Markierungen nach dem Auseinanderfalten auf eine Seite des Quadratischen Blattes übertragen.		 Skizze 1.2
Schritt 5: Erneutes schrittweises Falten zur Ermittlung von b und c in Abhängigkeit von a
 
Wird nun das Blatt Papier erneut nach der Anleitung und den bereits vorhandenen Knickfalten gefaltet, so ergibt sich ein neues Quadrat.
 
Die Kantenlänge dieses Quadrats sei d.
Durch die Falten lässt sich das quadratische Blatt in vier gleich große Quadrate mit Seitenlänge \(\frac { a }{ 2 } \) unterteilen.

Die Diagonale eines solchen Quadrats der Seitenlänge \(\frac { a }{ 2 } \) sei d.

 Skizze 1.3
Nun wird das Blatt weiter nach der Anleitung zur Mittelsenkrechten des Quadrats der Seitenlänge d gefaltet, sodass ein Rechteck mit den Seitenlängen d und \(\frac { d }{ 2 } \) entsteht.
Es ist erkennbar, dass \(b=\frac { d }{ 2 } \).
 
 Skizze 1.4
Ermittle nun b in Abhängigkeit von a.
 
In Skizze 1.3 ist zu erkennen, dass d die Hypotenuse eines gleichschenkligen rechtwinkligen Dreiecks mit Katheten der Länge \(\frac { a }{ 2 } \) ist. d lässt sich also mit dem Satz des Pythagoras berechnen:
 
  \( d^{ 2 }={ \left( \frac { a }{ 2 } \right) }^{ 2 }+{ \left( \frac { a }{ 2 } \right) }^{ 2 }\)
\(\Leftrightarrow \)    \( d² ={ \frac { a² }{ 4 } }+{ \frac { a² }{ 4 } }\)
\(\Leftrightarrow \) \({ d }^{ 2 }=\frac { 1 }{ 2 } { a }^{ 2 }\)
\(\Leftrightarrow \) \({ d }=\pm \frac { a }{ \sqrt { 2 } } \quad \quad \Rightarrow \quad \quad d=\frac { a }{ \sqrt { 2 } } \)
 
Durch Einsetzen von \(d=\frac { a }{ \sqrt { 2 } } \) in ergibt \(b=\frac { d }{ 2 } \) sich:    \(b=\frac { a }{ 2\sqrt { 2 } } \)
 
Es bleibt c in Abhängigkeit von a zu ermitteln. Dazu wird das Blatt wieder auseinandergefaltet. Eines der Quadrate mit Seitenlänge \(\frac { a }{ 2 } \) und Diagonale d lässt sich wiederum entlang der Knickfalten in vier kongruente Quadrate mit Seitenlänge \(\frac { a }{ 4 } \) unterteilen.
Bei Betrachtung eines solchen Quadrats lässt sich erkennen, dass die Diagonale eines solchen Quadrats \(\frac { d }{ 2 } \) ist und c die halbe Diagonale eines solchen Quadrats, also \(c=\frac { d}{ 4 } \) .
 
Mit \(d=\frac { a }{ \sqrt { 2 } } \) folgt \(c=\frac { a }{ 4\sqrt { 2 } } \).
 Skizze 1.5
Schritt 6: Einsetzen in die Volumenformel
Durch Einsetzen von \(b=\frac { a }{ 2\sqrt { 2 } } \) und \(c=\frac { a }{ 4\sqrt { 2 } } \) in die Volumenformel der Schachtel ergibt sich:
 
  \(V={ \left( \frac { a }{ 2\sqrt { 2 } } \right) }^{ 2 }\cdot \frac { a }{ 4\sqrt { 2 } } \)
\(\Leftrightarrow \)    \(V=\frac { a² }{ 8 } \cdot \frac { a }{ 4\sqrt { 2 } } \)
\(\Leftrightarrow \) \(V=\frac { 1 }{ 32\sqrt { 2 } } a³\)
                                  
 
 
 
Lösungsvariante 2: Geometrische Lösung durch Nutzen der Verhältnisse zwischen den Kanten des Quaders und der Seitenlänge a des quadratischen Blattes
 
 
Schritt 1 bis 4:
Wie bei Lösungsvariante 1.
 

                          
Schritt 5: Ermittlung von b und c in Abhängigkeit von a
Durch die Art und Weise wie die Schachtel gefaltet wurde, sind zwei Knickfalten entstanden, die das Quadrat der Seitenlänge a in vier kongruente Quadrate der Seitenlänge \(\frac { a }{ 2 } \) unterteilen. Zwei dieser vier Quadrate lassen sich durch weitere Knickfalten wiederum in vier kongruente Quadrate der Seitenlänge \(\frac { a }{ 4 } \) unterteilen.

Die Diagonale eines Quadrats der Seitenlänge \(\frac { a }{ 4 } \) entspricht der Kante b. b unterteilt ein solches Quadrat also in zwei gleichschenklige, rechteckige Dreiecke mit Hypotenuse b und Katheten \(\frac { a }{ 4 } \) .

Ein solches Dreieck wird von c in zwei gleichschenklige, rechtwinklige Dreiecke mit Hypotenuse \(\frac { a }{ 4 } \) und Katheten c unterteilt. 
Mit dem Satz des Pythagoras können nun also b und c direkt in Abhängigkeit von a ermittelt werden.
Berechnung von b:

 
  \(b²={ \left( \frac { a }{ 4 } \right) }^{ 2 }+{ \left( \frac { a }{ 4 } \right) }^{ 2 }\)
\(\Leftrightarrow \) \(b²=2\cdot \frac { a² }{ 16 } \)
\(\Leftrightarrow \)    \(b²=\frac { a² }{ 8 } \)
\(\Rightarrow \) \(b=\frac { a }{ 2\sqrt { 2 } } \)
Ermittlung von c:
  \({ \left( \frac { a }{ 4 } \right) }^{ 2 }=c²+c²\)
\(\Leftrightarrow \) \(\frac { a² }{ 16 } =2c²\)
\(\Leftrightarrow \) \(c²=\frac { a² }{ 32 } \)
\(\Rightarrow \)   \(c=\frac { a }{ 2\sqrt { 4 } } \)
Skizze 2.1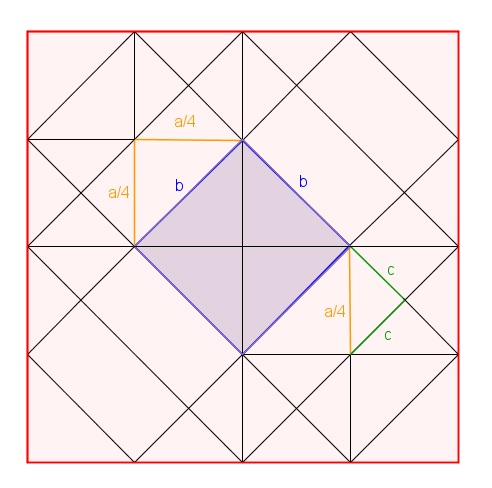
Schritt 6: Einsetzen in die Volumenformel
Wie beim vorherigen Lösungsweg.
 
 
 
 
Lösungsvariante 3: Geometrische Lösung durch Nutzen des Verhältnisses zwischen Grundfläche des Quaders und Fläche des Quadratischen Blattes 
 
Schritt 1: Falten der Schachtel
Wie bei den vorherigen beiden Lösungswegen.
 
 
Schritt 2: Volumenformel für die Schachtel
Das Volumen der Schachtel lässt sich mit der Volumenformel
\(V={ F }_{ S }\cdot h\) ,
wobei \({ F }_{ S }\) die Grundfläche der Schachtel und \(h\) die Höhe ist, berechnen.
 
Schritt 3: Markierung markanter Objekte
Die Grundfläche \({ F }_{ S }\) und die Höhe h werden auf der Box markiert.
(Auch hier sollten ggf. wieder alle markierten Linien nach Auseinanderfalten auf eine Seite des Quadratischen Blattes übertragen werden.)
 
Schritt 4: Auseinanderfalten um b² und h in Abhängigkeit von a zu ermitteln
Um einen Zusammenhang zwischen der quadratischen Grundfläche der Schachtel \({ F }_{ S }\) und der Fläche des quadratischen Blattes \({ F }_{ B }\) bzw. zwischen der Höhe h und der Seite a zu erkennen, wird die Schachtel wieder auseinandergefaltet.

Es lässt sich erkennen, dass sich die Grundfläche der Box aus vier kongruenten gleichschenkligen rechteckigen Dreiecken zusammensetzt, deren Hypotenuse b ist.

Betrachte ein solches Dreieck\(\Delta A'B'C'\) . Mit dem SWS-Satz lässt sich erkennen, dass dieses Dreieck kongruent zum Dreieck \(\Delta ABC\) ist.

Außerdem lässt sich erkennen, dass sich das quadratische Blatt in vier Quadrate mit Seitenlänge \(\frac { a }{ 2 } \) unterteilen lässt und sich ein solches Quadrat jeweils in vier Quadrate der Seitenlänge \(\frac { a }{ 4} \) unterteilen lässt. Daraus folgt das sich das Quadratische Blatt in 16 Quadrate der Seitenlänge \(\frac { a }{ 4 } \) zerlegen lässt.
\(\Delta ABC\) halbiert ein Quadrat der Seitenlänge \(\frac { a }{ 4} \), d.h. zwei zu \(\Delta ABC\) kongruente Dreiecke haben den Flächeninhalt \({ \left( \frac { a }{ 4 } \right) }^{ 2 }\).
Die Grundfläche der Schachtel besteht aus vier zu \(\Delta ABC\) kongruenten Dreiecken, somit ergibt sich für die Grundfläche der Schachtel:
\({ F }_{ S }=b²=\ { \left( \frac { a }{ 4 } \right) }^{ 2 }=\frac { a² }{ 8 } \)
 
Ermittlung von h mit dem Satz des Pythagoras analog zu Lösungsweg 2 ergibt:
\(h=\frac { a }{ 4\sqrt { 2 } }\)
Skizze 3.1
 
 
 
 
 
 
 
 
 
 
 
Skizze 3.2
Schritt 5: Einsetzen in die Volumenformel
Durch Einsetzen von \(b²=\frac { a² }{ 8 } \) und \(h=\frac { a }{ 4\sqrt { 2 } } \)in die Volumenformel für die Box ergibt sich:
\(V=\frac { a² }{ 8 } \cdot \frac { a }{ 4\sqrt { 2 } } =\frac { 1 }{ 32\sqrt { 2 } } a³\)
 
 
 
 
Lösungsvariante 4: Eine rechnerische Lösung unter Einbeziehung von Messungen (geringes kognitives Niveau)
 
Schritt 1 und 2:
Wie beim ersten und zweiten Lösungsweg.          
Skizze 4.1
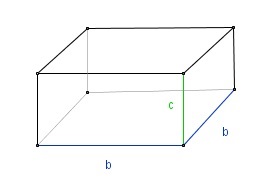Schritt 3: Abmessen markanter Größen
Durch Abmessung der ursprünglichen Seitenlänge a des Quadrats und der Kanten b und c der Box ergibt sich ungefähr:
a = 21,0 cm
b = 7,4 cm
c = 3,8 cm
Schritt 4: Größen in Relation zueinander setzen
Mithilfe der Messergebnisse können Verhältnisgleichungen aufgestellt werden:
  \(b=a\cdot x\quad \wedge \quad c=\cdot y\)
\(\Leftrightarrow \) \(x=\frac { b }{ a } \quad \wedge \quad y=\frac { c }{ a } \)
\(\Rightarrow \)    \(x=\frac { 7,4 }{ 21,0 } =\frac { 74 }{ 210 } \quad \wedge \quad y=\frac { 3,8 }{ 21,0 } =\frac { 38 }{ 210 } =\frac { 16 }{ 105 }\)
\(\Rightarrow \) \(b=\frac { 74 }{ 210 } a\quad \wedge \quad c=\frac { 16 }{ 105 } a\)
    
Schritt 5: Einsetzen in die Volumenformel
Einsetzen von \(b=\frac { 74 }{ 210 } a\) und \(c=\frac { 16 }{ 105 } a\) in die Volumenformel ergibt:
\(V={ \left( \frac { 74 }{ 210 } a \right) }^{ 2 }\cdot \frac { 16 }{ 105 } a=\frac { 703 }{ 11025 } a³\)
 

Die Origami-Aufgabe soll im Rahmen der Unterrichtssequenz Körperberechnung durchgeführt werden. Die Körperberechnung erfolgt an brandenburgischen Gymnasien in der Regel in der neunten Klasse, denn die SuS können in der Niveaustufe G, die der neunten Gymnasialklasse zugeordnet ist „geometrische Objekte beschreiben (auch Differenz- und Teilkörper sowie Differenz- und Teilflächen)“ (RLP, S.26) und sie können „Beziehungen zwischen geometrischen Objekten für Argumentationen nutzen“ (RLP, S.26).
Mit der Origami-Aufgabe werden jedoch Kompetenzen der Niveaustufen C bis E angestrebt (vgl. Kategorie "Geförderte Kompetenzen"). Laut RLP sollte am Ende der Grundschulzeit in der Jahrgangstufe 6 die Niveaustufe D erreicht sein. Niveaustufe E entspricht an Gymnasien der Klassenstufe 7 (vgl. RLP, S.16ff.). Somit könnte der Eindruck erweckt werden, dass diese Aufgabe einen zu geringen Anspruch an die Lernenden einer neunten Gymnasialklasse hat. Die Origami-Aufgabe soll jedoch zum Aktivieren von Vorwissen, zum Einstieg in die neue Thematik und zur Herstellung einer Verknüpfung von bereits erlernten geometrischen Zusammenhängen mit der neuen erweiternden Thematik dienen. Daneben hat die Aufgabe durch den Problemlösecharakter einen höheren Anspruch in den prozessbezogenen Kompetenzen. Die Jugendlichen müssen unter Verwendung bestimmter Heurismen (vgl. Kategorie „Heurismen“) selbständig eine Lösung des ihnen unbekannten Berechnungsproblems finden. Durch den niedrigeren inhaltlichen Anspruch werden die Schülerinnen und Schüler also vor keine allzu große inhaltliche Hürde gestellt, was sich positiv auf deren Motivation ausübt und keine abschreckende Wirkung nach sich zieht. Des Weiteren werden die Lernenden durch den feinmotorischen Aspekt des Faltens der Box geistig aktiviert und für den folgenden Unterricht motiviert. Eine solche eher ungewöhnliche Aufgabe bleibt den Jugendlichen im Gedächtnis.
In der darauffolgenden Unterrichtssequenz werden dann Volumen- und Flächenberechnungen weiterer mathematischer Körper thematisiert.
Durch die geringen geförderten Niveaustufen C bis E wird eine weitere Variante der Einbettung dieser Aufgabe in den Mathematikunterricht ermöglicht. So kann sie auch als Anwendungsaufgabe nach der Thematisierung des Satzes des Pythagoras in der 7. Klassenstufe an Gymnasien bearbeitet werden. Denn laut RLP können die Lernenden in Niveaustufe E „Beziehungen zwischen geometrischen Objekten beschreiben“ (RLP, S.26).

Inhaltzbezogene Kompetenzformulierungen
 
Größen und Messen
Die Schülerinnen und Schüler kennen die Volumenformel für Quader.
Größen und Messen, Niveaustufe D „Die Schülerinnen und Schüler können Größen messen (auch Volumina und Winkelgrößen)“ (RLP, S.24); Raum und Form, Niveaustufe C „Die Schülerinnen und Schüler können ausgewählte geometrische Objekte qualitativ beschreiben“ (RLP, S.26)
 
Raum und Form
Die Schülerinnen und Schüler wenden Sätze über spezielle Dreiecke an (z.B. den Satz des Pythagoras, die Kongruenzsätze SSS, SWS, WSW und SSW) und haben Kenntnisse über spezielle Linien in Quadraten und Dreiecken.
Raum und Form,  Niveaustufe D „Die Schülerinnen und Schüler können weitere geometrische Objekte qualitativ beschreiben“ (RLP, S.26); Niveaustufe E „Die Schülerinnen und Schüler können Beziehungen zwischen geometrischen Objekten beschreiben (auch Sätze über Dreiecke)“ (RLP, S.26)
 
Gleichungen und Funktionen
Die Schülerinnen und Schüler stellen eine Gleichung für das Volumen der quadratischen Schachtel in Abhängigkeit der Variablen a auf.
Gleichungen und Funktionen, Niveaustufe E „Die Schülerinnen und Schüler können Terme und Gleichungen darstellen (auch im Bereich der rationalen Zahlen)" (RLP, S.28)
 
 
 
Prozessbezogene Kompetenzformulierungen
 
Mathematisch argumentieren
Die Schülerinnen und Schüler entwickeln einen mehrschrittigen Lösungsweg, erkennen Strukturen und Zusammenhänge und können diesen mithilfe mathematischer Sätze wie z.B. dem Satz des Pythagoras begründen.
Mathematisch argumentieren, „Die Schülerinnen und Schüler können mehrschrittige Argumentationen zur Begründung und zum Beweisen mathematischer Aussagen entwickeln.“ (RLP, S.19)
 
Probleme mathematisch lösen
Die Schülerinnen und Schüler lösen eine ihnen unbekannte Aufgabe, zu der sie noch keine Routinestrategie kennen.
Probleme mathematisch lösen, „Die Schülerinnen und Schüler können Aufgaben bearbeiten zu denen sie noch keine Routinestrategien haben (sich zu helfen wissen).“ (RLP, S.19)
 
Die Schülerinnen und Schüler entwickeln eine Lösungsstrategie (z.B. kombiniertes Vorwärts- und Rückwärtsarbeiten, Analogieschlüsse oder Rückführung von Unbekanntem auf Bekanntes) und nutzen dabei Heuristische Hilfsmittel (Informative Figur, Skizze, Gleichungen) unter Verwendung heuristischer Prinzipien (z.B. Symmetrieprinzip). 
Probleme mathematisch lösen, „Die Schülerinnen und Schüler können Lösungsstrategien (z.B. vom Probieren zum systematischen Probieren) entwickeln und nutzen“ (RLP, S.19), „Die Schülerinnen und Schüler können heuristische Hilfsmittel zum Problemlösen anwenden.“ (RLP, S.19)
 
Mathematische Darstellungen verwenden
Die Schülerinnen und Schüler wechseln beim Finden der Formel mithilfe des Schachtel-Modells zwischen der räumlichen und der ebenen Geometrie und erstellen mithilfe von geometrischen Strukturen und Skizzen arithmetische Gleichungen.
Mathematische Darstellungen verwenden, “Die Schülerinnen und Schüler können eine Darstellung in eine andere übertragen“ (RLP, S.20), „Die Schülerinnen und Schüler können zwischen verschiedenen Darstellungen und Darstellungs-ebenen wechseln (übersetzen).“ (RLP, S.20)  
 
Mit symbolischen, formalen, technischen Elementen der Mathematik umgehen
Die Schülerinnen und Schüler verwenden die Volumenformel für Quader als Funktion des Volumens der Schachtel in Abhängigkeit der Variablen a. Sie führen weitere Variablen (hier b und c, bzw. b² und h) ein und ermitteln diese mithilfe von Gleichungen und Termen in Abhängigkeit der Variablen a.
Mit symbolischen, formalen, technischen Elementen der Mathematik umgehen, „Die Schülerinnen und Schüler können Tabellen, Terme, Gleichungen und Diagramme zur Beschreibung von Sachverhalten nutzen.“ (RLP, S.20), „Die Schülerinnen und Schüler können Variablen und Funktionen zur Bearbeitung von Aufgaben nutzen.“ (RLP, S.20)
 
Mathematisch kommunizieren
Die Schülerinnen und Schüler dokumentieren ihren eigenen Lösungsweg ausführlich beschreibend und begründend.
 
Die Schülerinnen und Schüler stellen den Mitschülerinnen und Mitschülern ihren Lösungsweg vor und vergleichen unterschiedliche Lösungswege miteinander.
Mathematisch kommunizieren, „Die Schülerinnen und Schüler können eigene Vorgehensweisen beschreiben, Lösungswege anderer nachvollziehen und gemeinsam Lösungswege reflektieren.“ (RLP, S.21), „Die Schülerinnen und Schüler können mathematische Zusammenhänge adressatengerecht beschreiben.“ (RLP, S.21), „Die Schülerinnen und Schüler können eigene Problembearbeitungen und Einsichten dokumentieren und darstellen.“ (RLP, S.21)
 
 
Die aufgeführten geförderten Kompetenzen beziehen sich auf die ersten drei Lösungswege. Beim vierten Lösungsweg werden die oben genannten Kompetenzen zwar auch erworben, der wesentliche Unterschied liegt jedoch im Anwenden der Heurismen (vgl. Kategorie "Heurismen"). Außerdem werden beim vierten Lösungsweg insbesondere folgende zusätzliche Kompetenzen gefördert:
 
Inhaltsbezogene Kompetenzformulierungen
 
Größen und Messen
Die Schülerinnen und Schüler können Längen messen.
Größen und Messen, Niveaustufe B, „Die Schülerinnen und Schüler können Längen messen“ (RLP, S.24)
 
Gleichungen und Funktionen
Die Schülerinnen und Schüler stellen die Verhältnisse (Verhältnis zwischen b und a bzw. c und a) zweier Längen in algebraischer Form dar.
Gleichungen und Funktionen, Niveaustufe E „Die Schülerinnen und Schüler können Terme und Gleichungen darstellen (auch im Bereich der rationalen Zahlen)“ (RLP, S.28)    
Zahlen und Operatoren
Die Schülerinnen und Schüler stellen das Verhältnis zweier Längen als rationale Zahlen dar.
Zahlen und Operatoren, Niveaustufe E „Die Schülerinnen und Schüler können Zahlenbeziehungen beschreiben (auch rationale Zahlen)“ (RLP, S.22)
 
 
 
Prozessbezogene Kompetenzformulierungen
Probleme mathematisch lösen
Die Schülerinnen und Schüler reflektieren ihren Lösungsweg und hinterfragen die Plausibilität von Ergebnissen kritisch.
Probleme mathematisch Lösen, „Die Schülerinnen und Schüler können Lösungswege reflektieren“ (RLP, S.19), „Die SuS können die Plausibilität von Ergebnissen überprüfen“ (RLP, S.19)
 
Mit den inhaltsbezogenen Kompetenzen wird der geringere Anspruch des vierten Lösungsweges deutlich. Allerdings können die Lernenden durch die Reflexion angeregt werden, einen anderen Lösungsweg zu finden. In diesem Fall würden sie sogar von diesem ersten kognitiv anspruchsloseren Lösungsweg profitieren, da sie das mathematische Problem aus verschiedenen Perspektiven betrachten.
 
 
 

Heuristische Hilfsmittel: 
  • Das quadratische Blatt, welches durch Falten in eine Schachtel transformiert wird, ist eine informative Figur. An diesem Modell kann die Lösungsidee das Blatt wieder auseinanderzufalten und dann Zusammenhänge zwischen Größen des Quaders und der Seitenlänge a des Blattes zu sehen, erkannt werden. Die Schachtel ist also gegeben und durch das markieren der Kanten der Schachtel und anschließendes Auseinanderfalten wird die informative Figur erzeugt - es entsteht eine zweidimensionale Skizze. Diese ist aber nur bei den ersten drei Lösungswegen von Bedeutung, bei der vierten Lösung wird die Struktur auf dem Blatt nicht genutzt.
 
  • Daneben werden Gleichungen benutzt. Zunächst wird das Volumen in Abhängigkeit von a in Form einer Funktionsgleichung dargestellt. Mithilfe weiterer Gleichungen werden dann Zusammenhänge zwischen markanten Größen der Box (hier c und b bei der ersten, zweiten und vierten Lösung, bzw. b² und h beim dritten Lösungsweg) und der Seitenlänge a des ursprünglichen Blattes dargestellt. Mithilfe dieser Gleichungen wird die allgemeine Volumenformel in Abhängigkeit von a ermittelt.
 
 
 
Heuristische Strategien: 
  • Das kombinierte Vorwärts- und Rückwärtsarbeiten ist bei der Origami-Aufgabe von besonderer Bedeutung. Gegeben ist die Seitenlänge a als allgemeine Variable. Gesucht ist V(a), also das Volumen der Schachtel in Abhängigkeit von a.
  1. Im ersten Schritt wird nun vorwärtsgearbeitet. Über das Gegebene ist bekannt, dass es sich bei der Schachtel um einen Quader mit quadratischer Grundfläche handelt und die Grundfläche und Kanten auf diesem markiert werden können und Variablen für diese eingeführt werden können. Außerdem ist bekannt, dass die Schachtel aus einem glatten quadratischen Blatt entstanden ist und somit wieder auseinandergefaltet werden kann. Durch das Falten hat sich die Struktur des Blattes verändert.
  2. Dann wird rückwärtsgearbeitet. Über das Gesuchte ist nun die Volumenformel für Quader bekannt, woraus sich \(V(a)=b²\cdot c\) (bzw.\(V(a)=b²\cdot h\) ) ergibt. Um das gesuchte zu ermitteln wird bei Lösung 3.1 und 3.2 das Verhältnis zwischen b und a bzw. c und a benötigt und bei Lösungsweg 3.3 das Verhältnis zwischen b² und a² bzw. h und a. Diese Verhältnisse können mithilfe der informellen Figur, also dem auseinandergefalteten Blatt ermittelt werden. Bei Lösung 4 werden Messwerte für das Aufstellen der Verhältnisgleichungen benutzt.
  3. Beim Ermitteln der Verhältnisse erfolgt also wieder ein vorwärtsarbeiten ausgehend vom auseinander gefalteten Blatt bzw. ausgehend von den Messwerten in Lösungsweg 4. Es lässt sich erkennen, dass die Struktur des Blattes die Anwendung bereits bekannter mathematischer Zusammenhänge aus der ebenen Geometrie ermöglicht. Bei allen drei Wegen wird der Satz des Pythagoras auf unterschiedliche Art und Weisen angewendet. Bei Weg 3.1 erfolgt das Vorwärtsarbeiten durch schrittweises erneutes Falten der Schachtel, wodurch bestimmte Längen begründet werden können. Bei Weg 3.2 wird nur der Satz des Pythagoras angewendet, daher ist dies auch der überschaubarste Weg. Und bei Weg 3.3 wird die Kongruenz bestimmter Dreiecke genutzt, um das Flächenverhältnis zwischen Grundfläche der Box und der Fläche a² zu ermitteln. Eine weitere Rolle spielt daneben bei allen drei Lösungswegen die Unterteilung des Blattes in Quadrate.
  4. Im letzten Schritt, dem Einsetzen der jeweiligen Verhältnisformeln in V(a) wird bei allen Lösungswegen wieder rückwärtsgearbeitet, da das Gesuchte betrachtet wird.
 
  • Es muss außerdem von Unbekanntem auf Bekanntes rückgeführt werden. Die Problemlösenden vermuten, dass auf dem auseinander gefalteten Blatt Strukturen zu erkennen sind, die ihnen in dem Sinne weiterhelfen, dass sie Analogien zu bereits durchgeführten Aufgaben und bereits bekannten Zusammenhängen entdecken (siehe nächster Aspekt „Analogieschluss“). Mit dem dreidimensionalen Modell sind keine Zusammenhänge zwischen Kantenlängen der Box und a zu erkennen. Deshalb wird das Raumproblem durch Auseinanderfalten der Schachtel zu einem Problem in der Ebene gemacht, in der bekannte Sätze angewendet werden können. Auch bei Lösungsweg 4 muss die Schachtel auseinandergefaltet werden, um die Seite a zu messen.
 
  • Bei Betrachtung des auseinandergefalteten Blattes wird nach Analogien gesucht. Bei der Thematisierung von Dreiecken und Quadraten in vorherigen Unterrichtseinheiten wurde bereits der Satz des Pythagoras und Kongruenzsätze ausführlich thematisiert und entsprechende Aufgaben von den SuS gelöst. Die Lernenden erinnern sich zurück, finden Parallelen und setzen Analogieschlüsse. Dies ist beim vierten Lösungsweg jedoch nicht der Fall.
 
 
 
Heuristische Prinzipien: 
  • Beim Erkennen bereits bekannter mathematischer Zusammenhänge auf dem auseinandergefalteten Blatt spielt das Symmetrieprinzip eine Rolle. Wie schon unter der Strategie des Analogieschlusses beschrieben, werden Analogien gefunden. Somit wird dieses Prinzip bei Lösungsweg 4 nicht angewandt.
 
  • Es wird nach der funktionalen Beziehung des Volumens der Schachtel in Abhängigkeit der Seitenlänge a gesucht. Dabei wird bei den ersten beiden Lösungswegen nach b und c in Abhängigkeit von a gesucht und beim dritten Lösungsweg nach b² und h in Abhängigkeit von a. Die Ermittlung dieser Verhältnisse erfolgt immer durch das Finden struktureller Zusammenhänge auf dem Blatt, also jeweils nach dem gleichen Prinzip. Darüber hinaus sind auf dem Blatt gleichlange Falten sowie kongruente Quadrate und Dreiecke zu sehen. Es gibt also unveränderte Größen und Formen in der Struktur. Somit spielt auch das Invarianzprinzip bei der Lösung eine Rolle. Bei der vierten Lösung werden die Verhältnisse zwischen b und a sowie c und a jeweils auf die gleiche Art und Weise ermittelt, daher wird das Prinzip auch bei diesem Lösungsweg verwendet.
 
  • Aufgrund der Umwandlung des dreidimensionalen Modells (Schachtel) in ein zweidimensionales Modell (quadratisches Blatt) wird auch das Transformationsprinzip verwendet.
 
 
 
Es wird deutlich, warum der vierte Lösungsweg ein niedrigeres kognitives Anspruchsniveau hat. Bei diesem Lösungsweg sind nur das heuristische Hilfsmittel „Gleichungen“, die Strategie „kombiniertes Vorwärts- und Rückwärtsarbeiten“ und das Invarianzprinzip beim analogen Vorgehen des Aufstellens der Verhältnisgleichungen von Bedeutung.

Eine Problemlöseaufgabe kann nach Cohors-Fresenborg et al gewisse Schwierigkeiten beinhalten. Diese unterscheiden sich bei der Origami-Aufgabe zwischen den ersten drei Lösungswegen und dem vierten bezüglich der Kognitiven Komplexität und der Formalisirung von Wissen.
 
Für die ersten drei Lösungswege ergibt sich mit den 6 erreichten Punkten eine Schwierigkeit von ***.
Für den vierten Lösungsweg ergeben sich insgesamt 2 Punkte. Die Aufgabe hat also mit dieser Lösung einen Schwierigkeitsgrad von *.
 
 
Sprachlogische Komplexität: 
Die Sprachlogische Komplexität der Aufgabe entspricht der Stufe 1, da die Aufgabe kurz und verständlich formuliert ist und keine komplexen Nebensätze vorhanden sind. Es wird nur nach der allgemeinen Volumenformel für die Schachtel in Abhängigkeit von a gefragt, woraus jedoch keine Rückschlüsse auf die Reihenfolge der Bearbeitung gemacht werden können. Außerdem handelt es sich um eine offene Frage, es wird nicht explizit nach der Volumenformel gefragt, sondern danach, ob es eine gibt. Dafür wird jedoch der Hinweis "i.a.W. V=V(a)" gegeben.
 
 
Kognitive Komplexität: 
Bezüglich der Kognitiven Komplexität hat die Problemlöseaufgabe für Lösungsweg 1 bis 3 die Stufe 2, da die Denkvorgänge durch heuristische und strukturierende Überlegungen wie das Kombinierte Vorwärts- und Rückwärtsarbeiten, das Schließen von Unbekanntem auf Bekanntem und dem Analogieschluss begleitet werden.
Für den vierten Lösungsweg hat die Problemlöseaufgabe jedoch nur die Stufe 0, da deutlich weniger Heurismen von Bedeutung sind (vgl. Kategorie "Heurismen") und nur „wenige Denkvorgänge nacheinander abzuarbeiten sind“ (Cohors-Fresenborg et al..2004.S.114).
 
 
 
Formalisierung von Wissen: 
Auch die Formalisierung von Wissen ist bei den ersten drei Lösungen auf Stufe 2 gefordert, da zur Lösung der Aufgabe einfache Darstellungskontexte zu erbringen sind (hier die Volumenformel in Abhängigkeit von a und dafür die Kantenlängen, bzw. die Grundfläche der Schachtel in Abhängigkeit von a). Darüber hinaus wird die Struktur des auseinandergefalteten Blattes durch das vorherige Markieren der Kanten und der Grundfläche auf der Schachtel wesentlich übersichtlicher. Diese Darstellung ist eigenständig zu Erbringen.
Beim vierten Lösungsweg erfolgt die Formalisierung auf Stufe 0, da für die Neuntklässler und -klässlerinnen „sehr einfache Darstellungskontexte“ (Cohors-Fresenborg et al..2004.S.116), nämlich die Verhältnisgleichungen, eigenständig erbracht werden.
 
 
 
Formelhandhabung: 
Die Formelhandhabung hat bei der Origami-Aufgabe einen Schwierigkeitsgrad der Stufe 1. Die zu erbringenden Termumformungen sind überschaubar und Gleichungen können durch einfache Vorgehensweisen umgeformt werden. Die Anzahl der Schritte ist überschaubar und zu benutzende Sätze stammen aus keinem allzu großen Formelrepertoire, da die Schülerinnen und Schüler noch nicht viele Sätze an Dreiecken kennen gelernt haben. Die Anwendung des Satzes des Pythagoras ist daher naheliegend. Somit entspricht das Niveau der Formelhandhabung nicht der zweiten Stufe. 
 
 
Stufenzuordnung: 
Formalisierung von Wissen
Stufe 0
Stufe 2
Formelhandhabung
Stufe 1
Kognitive Komplexität
Stufe 0
Stufe 2
Sprachlogische Komplexität
Stufe 1

Hilfestellungen: 
Am Anfang des Problemlöseprozesses kann es für die Lernenden ein Problem sein, auf die Idee zu kommen die Schachtel wieder zu entfalten, um mathematische Strukturen und Zusammenhänge zwischen den Kanten bzw. der Grundfläche der Schachtel und der Seitenlänge des Quadratischen Blattes zu erkennen. Die SuS können also Probleme beim Erzeugen der informellen Figur haben.
Allgemein-strategische Hilfen Inhaltsorientierte strategische Hilfen Inhaltliche Hilfen
Gibt es eine Möglichkeit, dass das haptische Modell Informationen über das Verhältnis der Kantenlängen gibt? Kann eine informelle Figur erzeugt werden?
Kannst du an der Box direkt Zusammenhänge zwischen den Kanten und der Seitenlänge a des quadratischen Blattes erkennen?
Welche mathematischen Sätze und Zusammenhänge sind dir aus der Geometrie bekannt? Welche geometrischen Objekte kannst du in diesem Modell wiedererkennen?
Denke daran, was zu Beginn gegeben war. Hat sich etwas durch den Faltprozess verändert?
Überlege dir, wie du bestimmte Längen in Abhängigkeit einer anderen Länge ermitteln kannst. Benötigst du bestimmte Hilfslinien?
Kannst du in diesem Modell ebene geometrische Objekte erkennen? Welche Form muss das Modell dafür haben?
Hilft es dir, Größen auf der Schachtel zu markieren, die für die Volumenberechnung notwendig sind?
Wie kannst du erkennen, ob du bekannte mathematische Sätze aus der Geometrie anwenden kannst? Was würde dir dabei helfen?
Welche Größen musst du in Abhängigkeit von a betrachten, um das Volumen der Schachtel in Abhängigkeit von a zu berechnen? Kannst du diese Größen mithilfe des Modells in einen mathematischen Zusammenhang bringen?
 
 
Im weiteren Lösungsprozess kann die Schwierigkeit auftreten, dass die Lernenden nicht auf die Idee kommen, welche mathematischen Zusammenhänge sie anwenden können, um die markierten Kanten bzw. die Grundfläche der Box in Abhängigkeit von der Seitenlänge a zu ermitteln. 
 
Allgemein-strategische Hilfen Inhaltsorientierte strategische Hilfen Inhaltliche Hilfen
Kennst du ähnliche Aufgaben? Was hat dir bei der Lösung geholfen?
Welche geometrischen Figuren kannst du erkennen? Welche mathematischen Sätze und Zusammenhänge kennst du bezüglich dieser? Helfen dir diese Sätze um Zusammenhänge zu ermitteln?
Wie kannst du die Länge der Hypotenuse von rechtwinkligen Dreiecken berechnen?
Markiere dir wichtige Linien.
Kannst du erkennen, wie die markierten Kanten der Box von der Seitenlänge a abhängen? Beachte das Faltmuster.
In welche Flächen wird das quadratische Blatt durch die Faltlinien unterteilt?
Kannst du Linien hervorheben oder ergänzen? Gibt es Linien der gleichen Größe?
Gibt es Linien der gleichen Länge? Wenn ja, wie kannst du das begründen?
Welche Linien gibt es in Quadraten? Welche Eigenschaften haben diese?
Erkenne eine Struktur! Erkenne Zusammenhänge zwischen den Linien!
  
Wann sind zwei Dreiecke kongruent?
 
 
Sozialformen: 
 
Einzelarbeit 
Partnerarbeit
 
 
Differenzierungsmöglichkeiten: 
Jeder Lernende ist zu Beginn der Aufgabenbearbeitung auf einem anderen kognitiven Niveau. So gibt es in fast jeder Lerngruppe leistungsschwächere und leistungsstärkere Schülerinnen und Schüler. Damit jeder Lernende in der Lage ist die Problemlöseaufgabe zu bearbeiten, muss sie möglichst an alle Kinder angepasst werden.
 
Für leistungsschwächere Schülerinnen und Schüler kann die Origami-Aufgabe folgender Maßen umformuliert werden:
 
Vereinfachung durch das Anschließen einer Frage:
Kann man eine allgemeine Formel für das Volumen der Box finden, wenn die Kantenlänge des quadratischen Blattes a ist (i.a.W. V=V(a))? Welchen Zusammenhang gibt es zwischen den Kantenlängen, bzw. der Grundfläche der Schachtel und a? Dokumentiere und begründe deine Lösung ausführlich!
 
Durch das „Nachfragen“ sollen die Schülerinnen und Schüler einen gedanklichen Anstoß zum Auseinanderfalten der Box bekommen. Man könnte auch andere zusätzliche Hilfen geben wie „Denke an bereits bekannte Sätze aus der ebenen Geometrie.“ Welche Frage oder Hilfestellung angeschlossen wird, ist von der Lerngruppe abhängig. Die Lehrkraft sollte die Kinder der Lerngruppe einschätzen können und eine auf die Lernenden bezogene hilfreiche Frage anschließen.
 
Veränderung durch Rahmenwechsel:
Das Berechnungsproblem kann durch Vorgabe der entsprechenden Volumenformel in ein Beweisproblem umgewandelt werden. Die Aufgabenstellung könnte lauten
Felix behauptet, dass die allgemeine Formel für das Volumen der Box in Abhängigkeit der Kantenlänge a des quadratischen Blattes \(V=\frac { 1 }{ 32\sqrt { 2 } } a³\)\(V(a)=\frac { 1 }{ 32\sqrt { 2 } } a³\) ist. Hat er recht? Beweise oder widerlege diese Aussage.
 
Vorteil dieser Umwandlung ist es, dass die Lernenden ein Ergebnis haben, an dem sie "festhalten" können. Wenn die Schülerinnen und Schüler zu diesem korrekten Ergebnis gelangen, wird ihnen Sicherheit gegeben, dass sie richtig vorgegangen sind und die Unsicherheit, die während der Bearbeitung der Berechnungsaufgabe auftreten kann, entfällt.
Durch diese Veränderung wird die Aufgabe jedoch ein Stück weit geschlossen, was sich negativ auf die Motivation auswirken kann. Die Lernenden werden nicht mehr neugierig gemacht, ob es tatsächlich eine Volumenformel in Abhängigkeit von a gibt, ihnen wird vielmehr nahegelegt, dass es auf jeden Fall eine solche Formel gibt.
Außerdem sollte darauf geachtet werden, dass bei der Einbettung kein Name verwendet wird, der in der Lerngruppe vorkommt, sondern ein neutraler Name gewählt wird.
 
 
Auch für leistungsstärkere Schülerinnen und Schüler gibt es Möglichkeiten der Veränderung:
 
Die Aufgabe kann geringfügig geändert werden:
Kann man eine allgemeine Formel für das Volumen der Box finden, wenn die Kantenlänge des quadratischen Blattes a ist? Dokumentiere und begründe deine Lösung ausführlich!
 
Hier wird nur auf den Hinweis „(i.a.W. V=V(a))“ verzichtet, wodurch die Lernenden die zusätzliche kognitive Leistung erbringen müssen, dass es sich um einen funktionalen Zusammenhang handelt, also dass V=V(a). Die Lernenden müssen also einen Darstellungswechsel von einer Formel zu einer funktionalen Darstellung in Abhängigkeit einer Variablen vollziehen.
 
Erhöhung des Schwierigkeitsgrades durch eine Einbettung in einen Kontext:

Felix möchte mit der gegebenen Anleitung eine Schachtel des Volumens 200,00cm³ aus einem quadratischen Blatt basteln, damit dort all seine Büroklammern Platz finden. Wie groß muss die Seitenlänge a des quadratischen Blattes mindestens sein, um eine solche Schachtel herzustellen?
 
Bei der Lösung dieser Aufgabe muss der oder die Lernende selbständig die Idee erbringen das Volumen erst einmal in Abhängigkeit von a zu ermitteln, um dann a berechnen zu können. Die Denkvorgänge müssen hier also in höherem Maße strukturiert werden. Darüber hinaus müssen die Schülerinnen und Schüler zusätzlich Kompetenzen in der Berechnung mit Einheiten (hier [cm³] und [cm]) aufweisen und in größerem Maße mit Gleichungen umgehen können.


Die Origami-Aufgabe kann als Einstiegsaufgabe in die Thematik Körperberechnung eingesetzt werden. Durch sie kann Vorwissen über den Satz des Pythagoras, über Dreiecke und Quadrate aktiviert werden und eine Überleitung von der ebenen Geometrie in die räumliche Geometrie auf forschende Weise geschaffen werden. Dieser Übergang lässt sich sogar visuell durch das Falten und Entfalten der Box nachvollziehen.
 
Auch als Beweisaufgabe könnte die Aufgabe nach entsprechendem Umformulieren verwendet werden (siehe Differenzierungsmöglichkeiten). In dieser Form kann sie insbesondere in das Themengebiet der Erarbeitung des Satzes des Pythagoras als Anwendungsaufgabe eingebettet werden. An dieser Stelle kann sie natürlich auch in der Originalformulierung in den Unterricht integriert werden.
 
Darüber hinaus kann sie auch als langfristige Hausaufgabe gestellt werden, sodass die verschiedenen Lösungsergebnisse im Unterricht nur noch besprochen werden müssen. Dies würde Unterrichtszeit einsparen, zieht aber die Gefahr mit sich, dass nicht alle Jugendlichen die Aufgabe tatsächlich bearbeitet haben. Dies wäre ein schlechter Einstieg in eine neue Thematik, da die Schülerinnen und Schüler nicht auf dasselbe Niveau gebracht werden und sich somit kognitive Differenzen von Anfang an besonders stark ausprägen können.


Bearbeitet von: Marisa Pfläging
nach oben
496 Nutzer/-innen haben abgestimmt.

Feedback

Wir freuen uns auf Ihre Anregungen und konstruktive Rückmeldung zum Material.