-
Email : info(at)proffi-m.de
Pferdekoppel
| Klasse | Schulstufe | Thema | Themengebiet | Schwierigkeit |
|---|---|---|---|---|
| 4/ 5/ 6 | Primarstufe | Flächeninhalt von Rechtecken | Größen und Messen, Raum und Form | **, *** |
| Heuristsche Hilfsmittel | Heuristische Prinzipien | Heuristische Strategien |
|---|---|---|
| Informative Figur, Gleichungen | Invarianzprinzip | Kombiniertes Vorwärts- und Rückwärtsarbeiten, Systematisches Probieren |
Aufgabenstellung
Max und Anna bekommen 2 Pferde. Bauer Hotte steckt mit 200 m Weidezaun eine rechteckige Pferdekoppel ab. Finde verschiedene Möglichkeiten, wie die Koppel aussehen kann. Wenn du zeichnest, zeichne so, dass 1 cm in der Zeichnung 10 m in der Wirklichkeit entsprechen. Wie groß ist die Fläche der jeweiligen Weide?
Quellenangabe:
In Anlehnung an Lorenz, J. (Hrsg.)(2008). Mathematikus 4. Braunschweig: Westermann. (S.26. Aufgabe 5)
gegeben:
|
gesucht: Fläche A der jeweiligen Weide
Lösungsweg 1 - Zeichnerische Lösung
|
Möglichkeit 1
|
\(A=10\cdot 90=900[m²]\) |
|
Möglichkeit 2
|
\(A=20\cdot 80=1600[m²]\) |
|
Möglichkeit 3
|
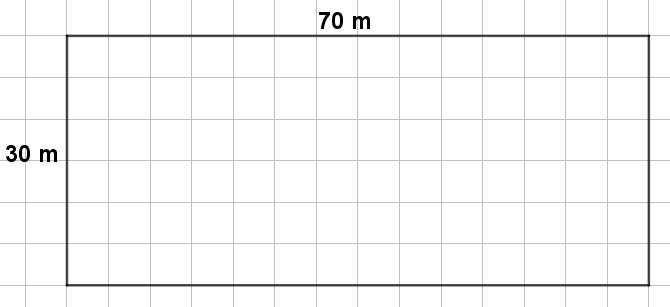
\(A=30\cdot 70=2100[m²]\) |
|
Möglichkeit 4
|
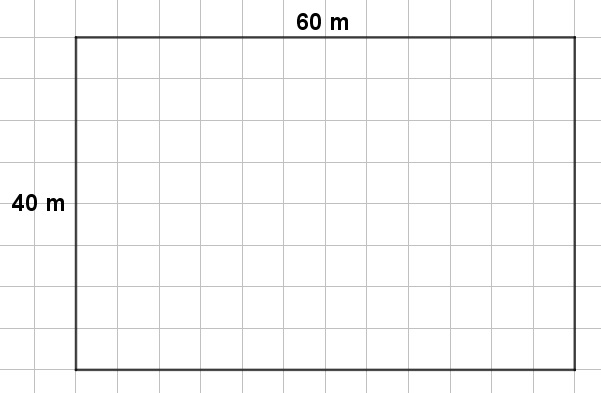
\(A=40\cdot 60=2400[m²]\) |
|
Möglichkeit 5
|
\(A=50\cdot 50=2500[m²]\)
(Bei dieser Möglichkeit ist die Koppel am größten.) |
Lösungsweg 2 - Rechnerische Lösung
Es seien x:= Länge der Koppel und y:= Breite der Koppel. Dann gilt für den Umfang der Koppel die folgende Formel:
|
\(\Leftrightarrow \) |
\(2(x+y)=200\) \(2x+2y=200\) |
Möglichkeit 1:
Es sei x=10.
| \(2\cdot 10+2y=200\) | ||
| \(\Leftrightarrow \) | \(20+2y=200\) | |\(-20\) |\(:2\) |
| \(\Leftrightarrow \) | \(y=90\) | |
| \(\rightarrow \) Flächeninhalt: \(A=10\cdot 90=900[m²]\) | ||
Möglichkeit 2:
Es sei x=20.
| \(2\cdot 20+2y=200\) | ||
| \(\Leftrightarrow \) | \(40+2y=200\) | |\(-40\) |\(:2\) |
| \(\Leftrightarrow \) | \(y=80\) | |
| \(\rightarrow \) Flächeninhalt: \(A=20\cdot 80[m²]\) | ||
Möglichkeit 3:
Es sei x=30.
| \(2\cdot 30+2y=200\) | ||
| \(\Leftrightarrow \) | \(60+2y=200\) | |\(-60\) |\(:2\) |
| \(\Leftrightarrow \) | \(y=70\) | |
| \(\rightarrow \) Flächeninhalt: \(A=30\cdot 70=2100[m²]\) | ||
Möglichkeit 4:
Es sei x=40.
| \(2\cdot 40+2y=200\) | ||
| \(\Leftrightarrow \) | \(80+2y=200\) | |\(-80\) |\(:2\) |
| \(\Leftrightarrow \) | \(y=60\) | |
| \(\rightarrow \) Flächeninhalt: \(A=40\cdot 60=2400[m²]\) | ||
Möglichkeit 5:
Es sei x=50.
| \(2\cdot 50+2y=200\) | ||
| \(\Leftrightarrow \) | \(100+2y=200\) | |\(-100\) |\(:2\) |
| \(\Leftrightarrow \) | \(y=50\) | |
|
\(\rightarrow \) Flächeninhalt: \(A=50\cdot 50=2500[m²]\) (Bei dieser Möglichkeit ist die Koppel am größten.) |
||
Die Aufgabe "Pferdekoppel" lässt sich ab der vierten Jahrgangsstufe im Rahmen der Unterrichtsthematik "Umfang und Flächeninhalt von Rechtecken" einsetzen. Maßstäbe werden zwar erst ab der siebten Jahrgangsstufe (Niveaustufe E, vgl. Abschnitt "Geförderte Kompetenzen") thematisiert, allerdings ist hier in der Aufgabenstellung vorgegeben, dass 10 m in der Realität als 1 cm auf dem Papier gezeichnet werden sollen, weshalb hier keine weiteren Umrechnungen von den Schülerinnen und Schülern gefordert werden. Die Befolgung dieser Anweisung kann demnach auch von Lernenden einer vierten Klasse erwartet werden.
Mit der Winkeldetektivaufgabe werden insbesondere der inhaltsbezogene Kompetenzbereich [L2] Größen und Messen sowie die prozessbezogenen Kompetenzbereiche [K2] Probleme mathematisch lösen, [K3] Mathematisch modellieren und [K4] Mathematische Darstellungen verwenden aus dem brandenburgischen Rahmenlehrplan (Teil C) Mathematik für die Jahrgangsstufen 1-10 (LISUM, 2015), der ab dem Schuljahr 2017/18 gültig ist, gefördert.
Inhaltsbezogene Kompetenzformulierungen
Größen und Messen [L2]
Kompetenz 1: Die Schülerinnen und Schüler berechnen den Umfang eines Rechtecks.
"Ermitteln des Umfangs von geradlinigen ebenen Figuren durch Auszählen von Einheitslängen" (LISUM, 2015, Größenangaben bestimmen, Niveaustufe C, S.40), "Ermitteln des Umfangs von ebenen Figuren durch Addition der einzelnen ausgemessenen Seitenlängen" (LISUM, 2015, Größen in Sachzusammenhängen berechnen, Niveaustufe C, S.41)
Erläuterung: Da Bauer Hotte 200 m Weidezaun zur Verfügung hat und die Koppel rechteckig sein soll, müssen die Kinder in der Lage sein, die Gesamtmeterzahl aufzuteilen, um so den Umfang berechnen zu können. Dafür brauchen sie Vorwissen über die Berechnung des Umfangs.
Kompetenz 2: Die Schülerinnen und Schüler ermitteln (mithilfe der Flächeninhaltsformel für Rechtecke oder durch Auszählen von Einheitsquadraten) den Flächeninhalt eines Rechtecks.
"Größen messen (auch [...] Flächeninhalte)" (LISUM, 2015, Größenangaben bestimmen, Niveaustufe C, S.24), "Ermitteln des ungefähren Flächeninhalts von geradlinigen ebenen Figuren durch Auszählen von Einheitsflächen" (LISUM, 2015, Größenangaben bestimmen, S.40), "Berechnen von Größenangaben (auch von Flächeninhalten [...] und auch in Dezimalschreibweise), insbesondere in Sachkontexten [...]" (LISUM, 2015, Größen in Sachzusammenhängen berechnen, Niveaustufe D, S.43)
Erläuterung: Der zweite Teil der Aufgabe erfordert es, die einzelnen Flächeninhalte zu berechnen. Dabei müssen die Lernenden wissen, wie die Fläche eines Rechtecks berechnet wird. Dies wird laut LISUM (2015) auf Niveaustufe D gefordert. Es ist aber auch möglich, dass die Schülerinnen und Schüler die Flächeninhalte in den einzelnen angefertigten Skizzen auszählen, sofern die Aufgabe mit dem ersten Lösungsweg gelöst wird. Dies würde den Anforderungen auf Niveaustufe C entsprechen.
Raum und Form [L3]
Kompetenz 3: Die Schülerinnen und Schüler erstellen maßstabsgetreue Zeichnungen eines Sachverhalts mithilfe eines vorgegebenen Maßstabs.
"Zeichnen von kongruenten sowie maßstäblich vergrößerten und verkleinerten ebenen Figuren zu vorgegebenen ebenen Figuren" (LISUM, 2015, Geometrische Abbildungen ausführen, Niveaustufe E, S.49)
Erläuterung: Da die Kinder bei der Zeichnung zehn Meter als einen Zentimeter darstellen sollen, müssen sie in der Lage sein, diese Umrechnung zu verstehen und durchzuführen.
Prozessbezogene Kompetenzformulierungen
Probleme mathematisch lösen [K2]
Kompetenz 4: Die Schülerinnen und Schüler lösen ein mathematisches Problem unter Verwendung geeigneter heuristischer Hilfsmittel (wie der Informativen Figur und der Gleichung) sowie heuristischer Strategien (wie dem Systematischen Ausprobieren und dem kombinierten Vorwärts- und Rückwärtsarbeiten).
"Die Schülerinnen und Schüler können Aufgaben bearbeiten, zu denen sie noch keine Routinestrategie haben (sich zu helfen wissen)" (LISUM, 2015, S.19), "Die Schülerinnen und Schüler können Lösungsstrategien (z. B. vom Probieren zum systematischen Probieren) entwickeln und nutzen heuristische Hilfsmittel zum Problemlösen anwenden" (ebd.)
Erläuterung: vgl. Abschnitt "Heurismen"
Mathematisch modellieren [K3]
Kompetenz 5: Die Schülerinnen und Schüler stellen die gegebene Situation mit den gesuchten Größen durch mathematische Darstellungen (wie Zeichnungen und Gleichungen mit Variablen) dar.
"Die Schülerinnen und Schüler können reale Situationen strukturieren und vereinfachen" (LISUM, 2015, S.20), "Die Schülerinnen und Schüler können Sachsituationen in die Sprache der Mathematik übersetzen" (ebd.), "Die Schülerinnen und Schüler können reale Situationen mit mathematischen Modellen beschreiben" (ebd.)
Erläuterung: In der Aufgabe müssen die mathematischen Begriffe in eine Zeichnung oder eine Gleichung übersetzt werden.
Mathematische Darstellungen verwenden [K4]
Kompetenz 6: Die Schülerinnen und Schüler verwenden graphische und mathematisch-symbolische Darstellungen zur Beschreibung eines gegebenen Sachverhalts.
"Die Mathematik bietet verschiedene, sich gegenseitig ergänzende Darstellungsformen: [...]
- grafische Darstellungen (z. B. Skizzen, Figuren, Funktionsgraphen)
- mathematisch-symbolische Darstellungen (z. B. Terme)
Mathematisches Arbeiten zeichnet sich durch Auswählen, Anfertigen und Interpretieren solcher Darstellungen aus." (LISUM, 2015, S.7)
Erläuterung: Beim ersten Lösungsweg stellen die Lernenden die verschiedenen rechteckigen Koppeln unter dem Maßstab 1:1000 grafisch dar. Zur Ermittlung des Flächeninhalts werden sowohl bei der zeichnerischen Lösung als auch bei der rechnerischen Lösung Gleichungen verwendet, wobei bei der zeichnerischen Lösung auch ein Abzählen der Kästchen möglich ist.
Heuristische Hilfsmittel:
- Bei der zeichnerischen Lösung werden Informative Figuren der möglichen Pferdekoppeln erstellt, aus denen auch der Flächeninhalt dieser durch Abzählen der Kästchen entnommen werden kann.
- Insbesondere bei der rechnerischen Lösung werden Gleichungen zur Bestimmung der zweiten Seitenlänge der Koppeln und zur Ermittlung des Flächeninhalts der jeweiligen Koppel genutzt. Auch beim ersten Lösungsweg können Gleichungen zur Berechnung des jeweiligen Flächeninhalts genutzt werden.
Heuristische Strategien:
- Bei den Aufgabenlösungen wird kombiniert vorwärts- und rückwärts gearbeitet: Es wird einerseits das Gesuchte (der Flächeninhalt der jeweiligen Weide) betrachtet und überlegt, was über das Gesuchte bekannt ist (der Umfang von 200 m, die Form der Koppel) und was benötigt wird, um das Gesuchte zu ermitteln (mögliche Seitenlängen). Ausgehend von diesen Überlegungen wird dann vorwärts gearbeitet, indem der Umfang fokussiert wird und die Umfangsformel, bzw. informative Figuren zur Ermittlung der Seitenlängen hinzugezogen werden und schließlich mit der Flächeninhaltsformel für Rechtecke der jeweilige Flächeninhalt berechnet wird.
- Bei beiden Lösungswegen wird systematisch probiert, indem die Seitenlängen des Rechtecks schrittweise (um 10 m) verkleinert, bzw. vergrößert werden.
Heuristische Prinzipien:
- Da sich der Umfang von Koppel zu Koppel nicht verändert und die Form der Koppeln rechteckig bleibt, wird das Invarianzprinzip beim systematischen Vorgehen angewendet.
Die Pferdekoppelaufgabe hat nach Cohors-Fresenborg et al. bezüglich des ersten Lösungsweges mit insgesamt 3 erreichten Punkten einen Schwierigkeitsgrad von ** und bezüglich des zweiten Lösungsweges mit insgesamt 7 erreichten Punkten einen Schwierigkeitsgrad von ***.
Sprachlogische Komplexität:
Da die Reihenfolge der Sätze den Schritten der mathematischen Bearbeitung nicht entspricht, es sich ansonsten aber um einfache Haupt- und Nebensätze handelt, in denen zum Teil ein Hinweis auf das heuristische Hilfsmittel der informativen Figur gegeben ist und in denen die unnötige Zusatzinformation, dass Max und Anna zwei Pferde bekommen, gegeben ist, lässt sich die Sprachlogische Komplexität der Aufgabe auf Stufe 1 ansiedeln.
Kognitive Komplexität:
Die kognitive Komplexität der Aufgabe lässt sich in Anbetracht des Einsatzes in einer vierten Klasse auf Stufe 2 anordnen, da sich die Lernenden vorher überlegen müssen, wie sie bei der Lösung der Aufgabe vorgehen und sie bei der Ermittlung der Flächen die Nebenbedingungen beachten müssen, dass die jeweilige Fläche rechteckig ist und einen Umfang von 200 m hat.
Formalisierung von Wissen:
Die Formalisierung von Wissen entspricht bezüglich des ersten Lösungsweges der Stufe 0, da hier der Flächeninhalt der jeweiligen Flächen lediglich rechnerisch ermittelt wird, aber nicht zwingend Gleichungen mit Variablen bei der Lösung aufgestellt werden müssen. Beim zweiten Lösungsweg erfolgt die Ermittlung der anderen Seitenlänge allerdings mithilfe der Umfangsgleichung für Rechtecke, die hier eigenständig zu erbringen ist. Im Anschluss daran wird mit der Gleichung zur Berechnung des Flächeninhalts von Rechtecken die Fläche bestimmt. Damit entspricht die Formalisierung von Wissen bezüglich des zweiten Lösungsweges der Stufe 2.
Formelhandhabung:
Auch die Formelhandhabung entspricht bezüglich des ersten Lösungsweges der Stufe 0, da lediglich bei der Berechnung des Flächeninhalts das Produkt aus den beiden Seitenlängen ermittelt wird. Bezüglich des zweiten Lösungsweges lässt sich auch die Formelhandhabung in Anbetracht einer Grundschulklasse auf Stufe 2 anordnen, da die Umfangsformel nach einer Variablen in mehreren Schritten umgeformt wird. Der Umgang mit Variablen und Gleichungsumformungen sind laut LISUM (2015, S.54) allerdings erst auf Niveaustufe D und E vorgesehen, weshalb Grundschülerinnen und -schüler diesen Weg wahrscheinlich nicht gehen werden.
Stufenzuordnung:
Formalisierung von Wissen
Stufe 0
Stufe 2
Formelhandhabung
Stufe 0
Stufe 2
Kognitive Komplexität
Stufe 2
Sprachlogische Komplexität
Stufe 1
Hilfestellungen:
Bei der Lösung der Pferdekoppel-Aufgabe lassen sich einige kritische Stellen identifizieren, an denen die Schülerinnen und Schüler Schwierigkeiten haben könnten.
Die Schülerinnen und Schüler könnten Probleme haben, den Umfang der Koppel zu berücksichtigen und durch Überlegungen über die Definition des Umfangs eines Rechtecks mögliche Seitenlängen des Rechtecks zu ermitteln. Tritt diese Problematik auf, so können folgende Hilfestellungen gegeben werden:
| Allgemein-strategische Hilfen | Inhaltsorientierte strategische Hilfen | Inhaltliche Hilfen |
| Schreibe dir alle wichtigen Informationen aus der Aufgabenstellung heraus. | Welche mathematischen Größen treten in der Aufgabenstellung auf? | Welcher mathematischen Größe entspricht die Länge des Weidezauns? |
| Was ist gegeben und was ist gesucht? | Welche Größen benötigst du zur Berechnung des Flächeninhalts? | Wie ist der Umfang eines Rechtecks definiert? |
| Fertige eine Skizze von der Koppel an! | Wie kannst du die zur Lösung notwendigen Größen ermitteln? | Wie ist der Flächeninhalt eines Rechtecks definiert? |
Eine weitere Schwierigkeit könnte darin bestehen, zunächst eine Seitenlänge des Rechtecks festzulegen und dann mithilfe des Umfangs der Koppel die andere Seite zu ermitteln. Ist dies der Fall so können den Schülerinnen und Schülern folgende Hilfen gegeben werden:
| Allgemein-strategische Hilfen | Inhaltsorientierte strategische Hilfen | Inhaltliche Hilfen |
| Gehe systematisch vor! | Lege eine Seitenlänge fest und bestimme die zugehörige andere Seitenlänge! | Welche Seitenlängen kommen für die Koppel in Frage? |
| Probiere aus, indem du Skizzen für die Koppeln machst! | Welche Größen kannst du durch die gegebene Gesamtlänge des Zauns festlegen? | Wie kannst du die andere Seitenlänge ermitteln, wenn eine Seitenlänge festgelegt ist? Überlege dir dazu, wie der Umfang eines Rechtecks definiert ist. |
Sozialformen:
- Einzelarbeit
- Partnerarbeit
Differenzierungsmöglichkeiten:
Sowohl für leistungsschwächere als auch für leistungsstärkere Schülerinnen und Schüler lässt sich die Aufgabe so abwandeln, dass weder die leistungsschwächeren Lernenden überfordert noch die leistungsstärkeren Lernenden unterfordert sind.
Mögliche Abänderungen der Aufgabenstellung für leistungsschwächere Schülerinnen und Schüler:
- Es könnten die verschiedenen Zeichnungen der Weiden-Varianten vorgegeben werden, sodass die Schülerinnen und Schüler diese nur noch ausmessen müssten.
- Den Lernenden können Hilfekärtchen für den Flächeninhalt und/oder den Umfang eines Rechtecks gegeben werden, die sie aufdecken können, wenn ein Fortschreiten im Lösungsprozess daran scheitert, dass sie sich nicht mehr an die entsprechende Gleichung erinnern können.
Beispiel-Kärtchen für den Umfang:
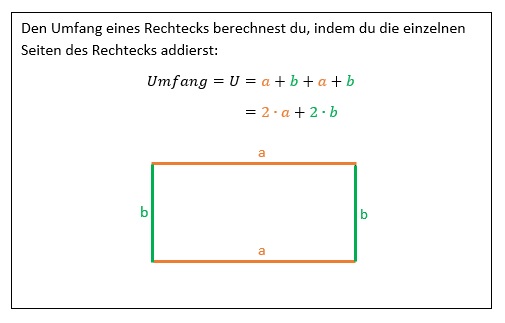
Beispiel-Kärtchen für den Flächeninhalt:
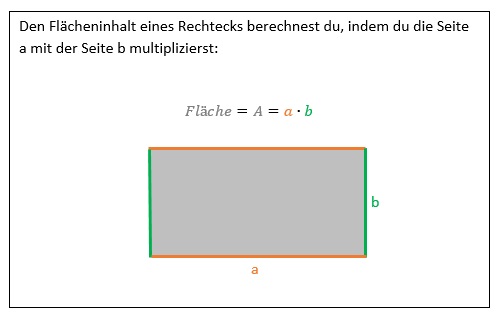
Mögliche Abänderungen der Aufgabenstellung für leistungsstärkere Schülerinnen und Schüler:
- Es könnte die Zusatzaufgabe "Wann ist die Weide am größten?" gestellt werden. Hier müssten die Schülerinnen und Schüler alle möglichen rechteckigen Flächen mit einem Umfang von 200 m finden und die verschiedenen Flächeninhalte miteinander vergleichen, um die größte Weide herauszusuchen. Hier wäre es allerdings sinnvoll, vorzugeben, dass die Seitenlängen nur ganzzahlige Vielfache von Zehn sein dürfen, um die Möglichkeiten zu begrenzen. (Ansonsten wäre die Aufgabe für Schülerinnen und Schüler der Grundschule nicht lösbar, da es sich durch diese zusätzliche Frage um eine Extremwertaufgabe handelt, die laut LISUM (2015, S.57) erst auf Niveaustufe H, also in der zehnten gymnasialen Jahrgangsstufe lösbar ist.)
- Es könnte die Zusatzaufgabe "Bauer Hotte zieht um. Nun liegt das Grundstück am Fluss, wo er keinen Zaun braucht. Wie groß kann er nun mit seinem 200m-Weidezaun seine Koppel stecken?" (Abwandlung von Mathematikus 4, S. 26, Aufgabe 6). Hier müssten die Schülerinnen und Schüler den Umfang auf nur 3 Seiten verteilen, da der Fluss die vierte Seite begrenzt. Dabei müssen sie ihr Wissen über die Umfangsberechnung auf den neuen Sachverhalt übertragen, um zu einem Ergebnis zu kommen.
Diese Aufgabe eignet sich für das Produktive Üben. Dabei kann das vorab erworbene Wissen über die Umfangs- und Flächenberechnung gefestigt werden, wobei mit dem Vorwissen und themenspezifischen Wissen aktiv geübt wird.
Bearbeitet von: Mona Aulenbacher, Annika Behling, Claire Gerecke, Julia Oker (ergänzt von Marisa Pfläging)
Feedback
Wir freuen uns auf Ihre Anregungen und konstruktive Rückmeldung zum Material.
Copyright © 2014-2017 - Ana Kuzle