-
Email : info(at)proffi-m.de
Polygone aus Streichhölzern
Fehlermeldung
Deprecated function: The each() function is deprecated. This message will be suppressed on further calls in FieldCollectionItemEntity->fetchHostDetails() (Zeile 313 von /www/htdocs/w0127817/beta.proffi-m.de/sites/all/modules/field_collection/field_collection.entity.inc).| Klasse | Schulstufe | Thema | Themengebiet | Schwierigkeit |
|---|---|---|---|---|
| 5/ 6/ 7/ 8/ 9/ 10 | Sekundarstufe I | Flächeninhalt von Polygonen bestimmen | Größen und Messen, Raum und Form | ** |
| Heuristsche Hilfsmittel | Heuristische Prinzipien | Heuristische Strategien |
|---|---|---|
| Informative Figur, Gleichungen | Zerlegungs- und Ergänzungsprinzip, Invarianzprinzip | Kombiniertes Vorwärts- und Rückwärtsarbeiten, Systematisches Probieren |
Aufgabenstellung
|
Es sind zwölf Streichhölzer zur konkreten Darstellung der einzelnen Teilprobleme nötig. Die Anfangssituation ist die folgende: Mit zwölf Streichhölzern lässt sich ein Quadrat mit einem Flächeninhalt von 9 FE (=Flächeneinheiten) legen.
Aus dieser Situation heraus lässt sich eine Folge von Problemen (= ein Problemfeld) entwickeln. Die Hauptidee dieses Problemfelds besteht darin, dass der Umfang des Polygons immer konstant bleibt, während der Flächeninhalt variiert. Der Umfang soll also stets 12 Streichhölzer betragen. Eine mögliche Folge von Problemen finden Sie unten:
|
Quellenangabe:
Pehkonen, E. (2001). Offene Probleme: Eine Methode zur Entwicklung des Mathematikunterrichts. Der Mathematikunterricht, 6, 60–72.
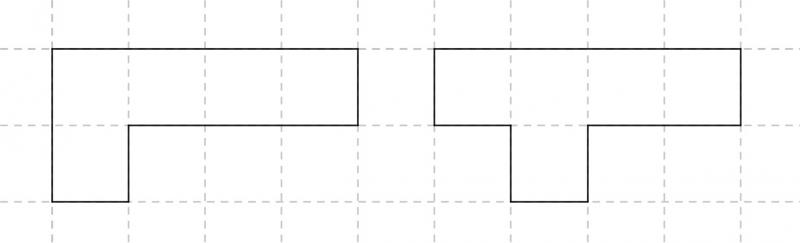
1. Lässt sich aus zwölf Streichhölzern ein Polygon mit einem Flächeninhalt von 5 FE herstellen?
| Ja, man könnte beispielsweise die folgenden beiden Polygone mit den geforderten Eigenschaften konstruieren: | |
| Lösungsmöglichkeit 1: | Lösungsmöglichkeit 2: |
|
|
|
| Für genauere Erklärungen und der Vorstellung einer systematischen Lösungsstrategie sei auf den Aufgabenteil 2 verwiesen. | |
2. Wie viele verschiedene Polygone mit einem Flächeninhalt von 5 FE können aus zwölf Streichhölzern erzeugt werden? Gibt es mehr als zehn verschiedene Lösungen?
Im Folgenden entspricht die Länge eines Streichholzes der Länge eines Kästchens im Rechengitter. Um nach Polygonen mit einem Flächeninhalt von 5 FE zu suchen, ist es am einfachsten, nach Polygonen zu suchen, die derart gestaltet sind, dass zwölf Streichhölzer nur waagerecht oder senkrecht (und demnach genau auf den Gitterlinien) liegen und diese gleichzeitig fünf der Rechenkästchen umschließen.
|
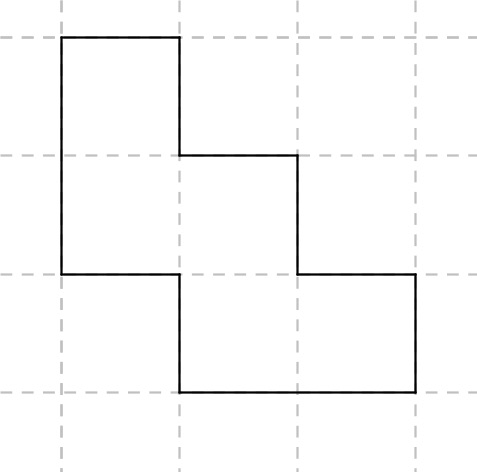
1. Geht man systematisch vor, kann man zunächst, den Fall betrachten, dass alle 5 Kästchen in einer Reihe liegen. |
|
|
2. Danach werden die Polygone betrachtet, die aus vier in einer Reihe liegenden Kästchen und einem weiteren bestehen, das an zwei verschiedenen Stellen an die vier in Reihe liegenden Kästchen angehängt werden kann. Würde man das fünfte Kästchen in eine Reihe mit den anderen vier Kästchen bringen, läge der erste bereits aufgeführte Fall von fünf in einer Reihe liegenden Kästchen vor. Würde man das fünfte Kästchen an einer der beiden bisher nicht berücksichtigten Stellen in der unteren Reihe platzieren, wären das entstehende Polygon durch eine Achsenspiegelung in eines der beiden bereits unter dem Punkt 2 aufgeführten Polygone überführbar. Würde man versuchen, das Kästchen über den vier in einer Reihe liegenden Kästchen zu platzieren, wäre das entstehende Polygon durch eine Drehung oder durch eine Kombination einer Drehung und einer Achsenspiegelung in eine der bereits unter 2 aufgeführten beiden Polygone überführbar. |
|
|
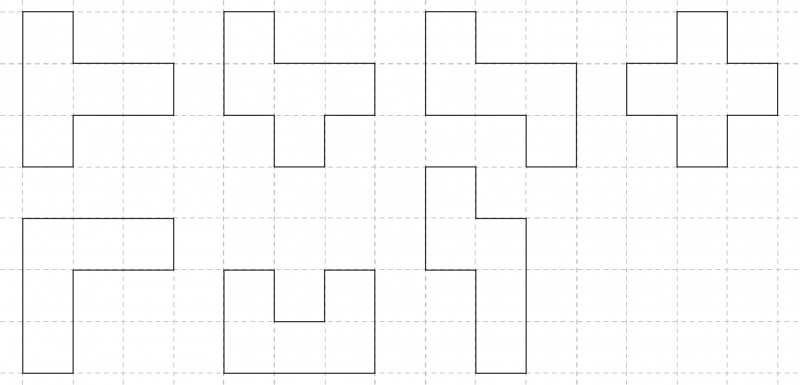
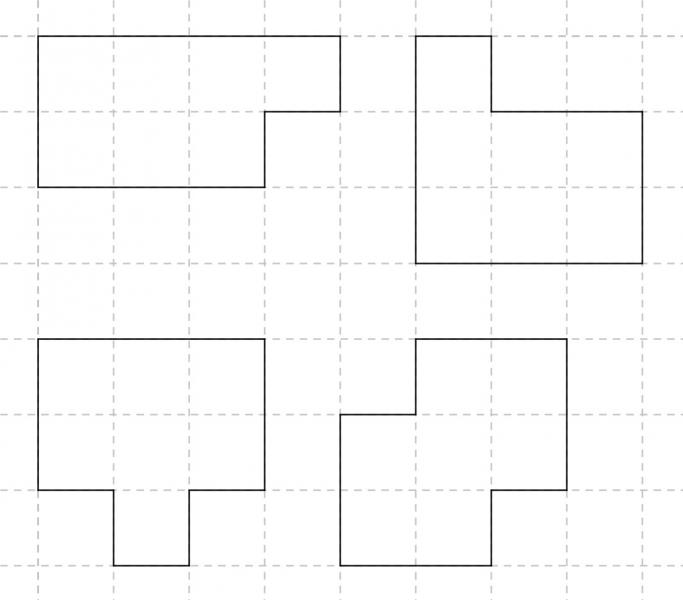
3. Sucht man dann Polygone mit einem Flächeninhalt von 5 FE, die sich aus drei in einer Reihe liegenden Kästchen und zwei weiteren Kästchen zusammensetzen, lassen sich die folgenden sieben Polygone finden.
Dabei entstehen die Polygone aus der oberen Reihe, wenn man die aus drei Kästchen bestehende Reihe als fixiert ansieht und jeweils ein Kästchen über und eines unter dieser Reihe anbringt. Die drei Polygone aus der unteren Reihe entstehen, wenn man an die aus drei Kästchen bestehende Reihe die beiden übrigen Kästchen an derselben Seite in verschiedenen Kongurationen platziert. Alle übrigen auf diese Weise konstruierten Polygone sind durch Drehungen, Achsenspiegelungen oder eine Kombination aus Drehungen und Achsenspiegelungen in unter dem Punkt 3 aufgeführte Polygone überführbar.
|
|
|
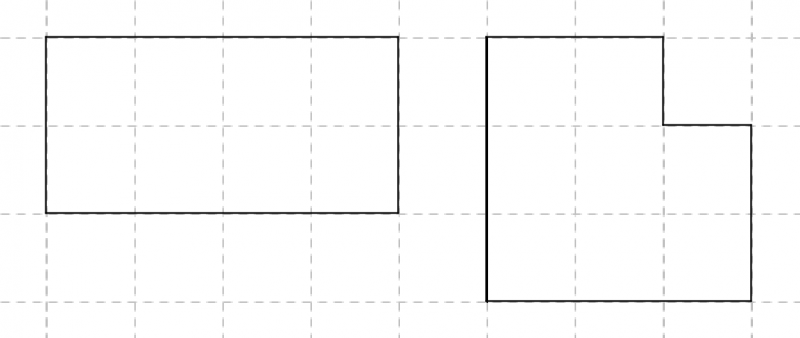
4. Zu den bereits gefundenen Polygonen ist ein weiteres zu nennen, das aus zweimal zwei Kästchen in einer Reihe und einem einzelnen Kästchen besteht. |
|
Mit diesem Vorgehen können elf verschiedene Polygone angegeben werden. Folglich kann die Frage, ob es mehr als zehn verschiedene Lösungen gibt, bejaht werden. Es ist allerdings davon auszugehen, dass es weitere Polygone gibt, die ebenfalls mit einem Umfang von 12 LE einen Flächeninhalt von 5 FE aufweisen, vor allem, wenn man bedenkt, dass bisher angenommen wurde, dass die Streichhölzer auf den Rechenkästchen liegen. Die Frage nach der Anzahl der Streichhölzer kann demnach bisher unpräzise mit mindestens elf beantwortet werden. Um alle Lösungsmöglichkeiten zu finden, müsste man alle denkbaren geometrischen n-eckigen Figuren durchgehen und prüfen, ob sie mit der gegebenen Anzahl an Streichhölzern nachgelegt werden können. Wenn ja, müsste der Flächeninhalt der so konstruierten Polygone berechnet werden. Aber auch bei diesem Verfahren kann man nicht ausschließen, Lösungen zu übersehen.
3. Ist es möglich, aus zwölf Streichhölzern ein Polygon mit einem Flächeninhalt von 6 FE (7 FE; 8 FE) herzustellen?
Alle Fälle sind möglich. Man kann solche Polygone finden, indem man sich sechs, sieben oder acht Rechenkästchen vorgibt und diese so zusammenhängend anordnet, dass ihr Umfang genau 12 LE beträgt. Dabei sind Polygone mit dem Flächeninhalt von n FE, mit n = {6, 7, 8}, besonders einfach zu finden, wenn man ausgehend von einem Polygon mit dem Flächeninhalt von n–1 FE zwei Streichhölzer so umlegt, dass genau ein neues Rechenkästchen zusätzlich von den Streichhölzern umschlossen wird.
|
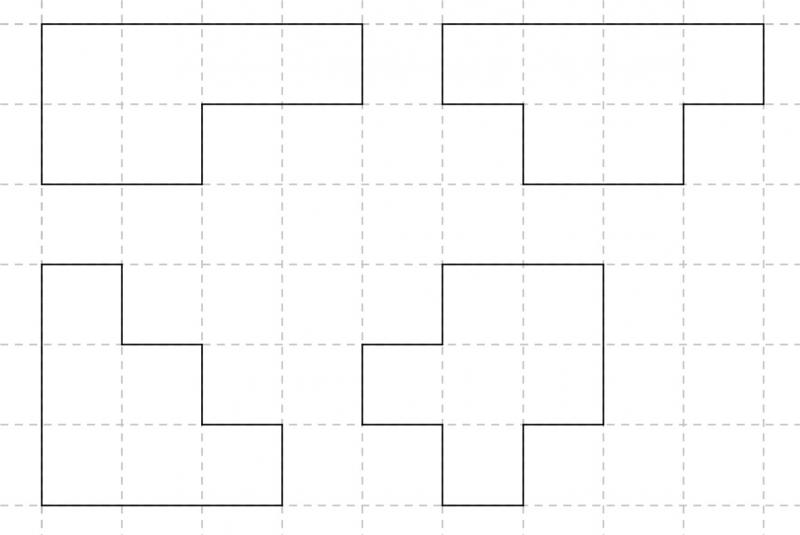
Beispiele für aus zwölf Streichhölzern gelegte Polygone mit einem Flächeninhalt von 6 FE finden Sie rechts. Die ersten beiden Konstruktionen ergeben sich dabei, wenn man zwei Streichhölzer aus den unter 2.2 gefundenen Polygonen mit einem Flächeninhalt von 5 FE umklappt, die dritte auf dieselbe Weise aus dem unter 2.4 aufgeführten Polygon mit einem Flächeninhalt von 5 FE und die vierte entsprechend aus dem vierten Polygon in der oberen Reihe der unter 2.3 aufgeführten Polygone mit einem Flächeninhalt von 5 FE. |
|
|
Beispiele für aus zwölf Streichhölzern gelegte Polygone mit einem Flächeninhalt von 7 FE finden Sie rechts. Die erste Konstruktion ergibt sich durch Umklappen zweier Streichhölzer aus den beiden Konstruktionen aus der oberen Reihe der Beispiele für Polygone mit einem Flächeninhalt von 6 FE. Entsprechend ergibt sich die zweite Konstruktion aus dem ersten Polygon aus der unteren Reihe der Beispiele für Polygone mit einem Flächeninhalt von 6 FE und die letzten beiden Konstruktionen aus dem zweiten Polygon aus derselben Reihe. |
|
|
Beispiele für aus zwölf Streichhölzern gelegte Polygone mit einem Flächeninhalt von 8 FE finden Sie rechts. Die erste Konstruktion ergibt sich durch Umklappen zweier Streichhölzer des ersten Polygons aus der ersten Reihe der Beispiele für Polygone mit einem Flächeninhalt von 7 FE. Entsprechend ergibt sich die zweite Konstruktion aus allen übrigen drei angegebenen Polygonen mit einem Flächeninhalt von 7 FE. |
|
4. Ist es möglich, mit Hilfe von zwölf Streichhölzern ein Polygon mit einem Flächeninhalt von 4 FE (3 FE; 2 FE; 1 FE) zu bauen?
Konstruktionsmöglichkeit 1 (für Polygone mit einem Flächeninhalt von (5 FE,) 4 FE und 3 FE):
| Man kann Polygone mit einem Flächeninhalt von 5 FE, 4 FE und 3 FE ausgehend von einem rechtwinkeligen Dreieck konstruieren, wenn die Katheten die Länge 3 LE und 4 LE besitzen. Die Hypotenuse besitzt dann nach dem Satz des Pythagoras die Länge 5 LE, sodass der Umfang des Dreiecks 12 LE beträgt und demnach mit 12 Streichhölzern nachgelegt werden kann. Ausgehend von den beiden denkbaren Dreiecken kann man immer zwei Streichhölzer so umlegen oder umklappen, dass sich der Ausgangsflächeninhalt von 6 FE in jedem Schritt um 1 FE verkleinert. Dieses sukzessive Umklappen zweier Streichhölzer ist in der Abbildung dargestellt. Mit dem vorgegebenen Dreieck lassen sich so Polygone mit den Flächeninhalten 5 FE, 4 FE und 3 FE konstruieren. |  |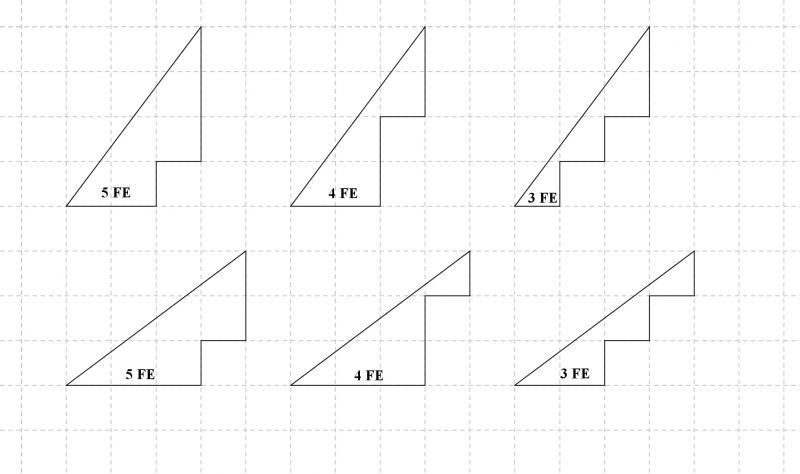
Konstruktionsmöglichkeit 2 (für Polygone mit einem Flächeninhalt von 4 FE und 3 FE):
| Polygone aus zwölf Streichhölzern und einem Flächeninhalt von 4 FE und 3 FE können in Form von Parallelogrammen konstruiert werden. Da nach dem Satz des Pythagoras 32+42 = 52 gilt, kann mithilfe von zwei Katheten der Längen 3 LE und 4 LE, die auf dem Rechengitter liegen, als Hypotenuse eine Strecke der Länge 5 LE konstruiert werden, die nicht auf diesem Gitter liegt. Auf diese Weise können zwei Parallelogramme (in der Zeichnung gefärbt) konstruiert werden, deren Grundseite der Länge eines Streichholzes und demnach 1 LE entspricht und deren Höhe 4 LE bzw. 3 LE entspricht, sodass der Flächeninhalt wegen 1·4 = 4 bzw. 1·3 = 3, 4 FE bzw. 3 FE beträgt. Die Seiten des Parallelogramms, die nicht auf dem Rechengitter liegen, besitzen nach Konstruktion mithilfe des rechtwinkeligen Dreiecks die Länge 5 LE und bestehen demnach aus jeweils fünf Streichhölzern, sodass die entstehenden Parallelogramme aus insgesamt 12 Streichhölzern bestehen. |  |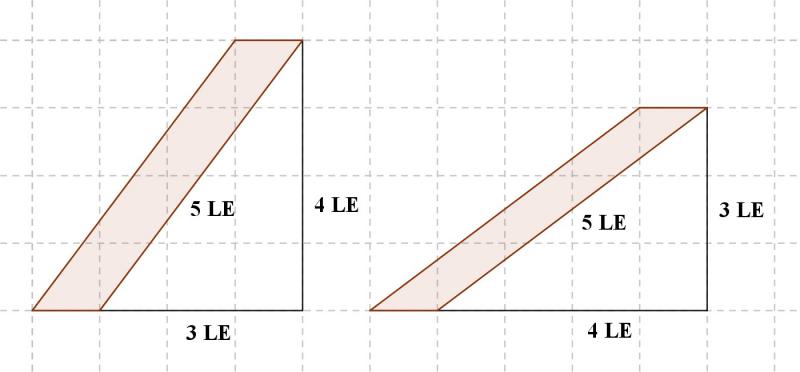
| Versucht man, Polygone aus zwölf Streichhölzern und einem Flächeninhalt von 2 FE und 1 FE analog zu konstruieren, muss man zunächst Strecken der Länge 1 LE und 1 LE konstruieren um diese jeweils als eine Kathete des Dreiecks verwenden zu können. Die zweite Kathete besitzt dann die Länge 2 LE bzw. 1 LE, während die Hypotenuse wie zuvor die Länge 5 LE besitzt. Prinzipiell sind solche Konstruktionen möglich. | |
Konstruktionsmöglichkeit 3 (für Polygone mit einem Flächeninhalt von 4 FE, 3 FE, 2 FE und 1 FE):
|
Im Allgemeinen lassen sich Polygone mit einem Flächeninhalt von 4 FE, 3 FE, 2 FE und 1 FE als Parallelogramme mit Grundseiten der Länge 4 LE, 3 LE, 2 LE oder 1 LE und Höhen der Länge 1 LE konstruieren. Es sei x die Maßzahl des gewünschten Flächeninhalts des Parallelogramms. Zuerst legt man die Grundseite aus x Streichhölzern. Wir betrachten als Beispiel zunächst den Fall x = 4. Dann berechnet man die Länge der beiden anderen Seiten des Parallelogramms mit der Umfangsformel \(u=2\cdot a+2\cdot b\) mit den Variablen a und b für die beiden Seitenlängen des Parallelogramms. Durch Umformen ergibt sich:
|
 |
||||||
| Ein Parallelogramm mit einem Flächeninhalt von 3 FE ist analog konstruierbar: |  |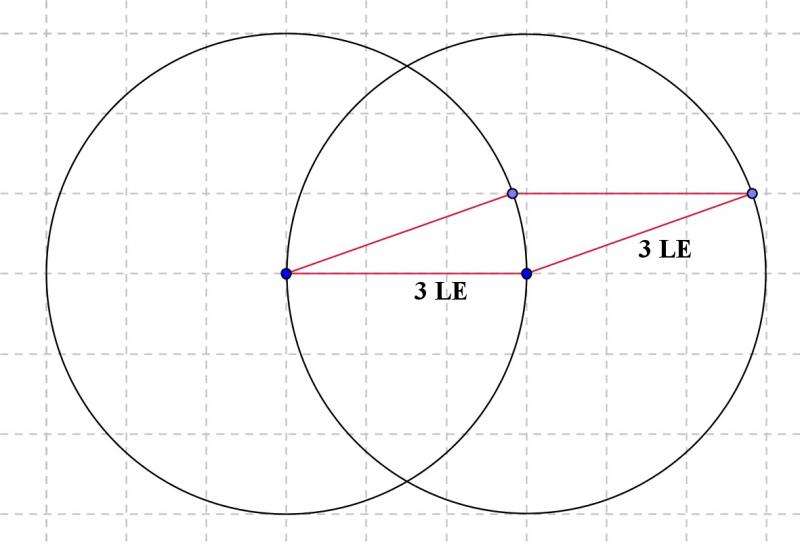
||||||
| Ebenso wie ein Parallelogramm mit einem Flächeninhalt von 2 FE: |  |
||||||
| Auch ein Parallelogramm mit einem Flächeninhalt von 1 FE ist auf diese Weise konstruierbar: |  |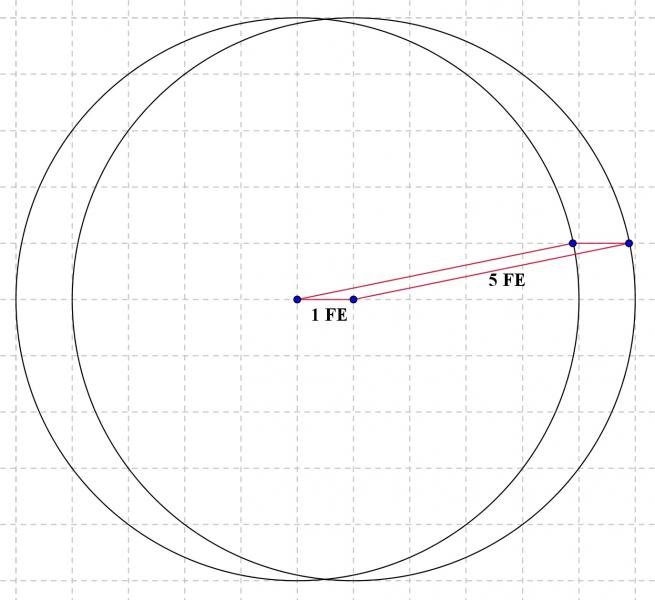
5. Ist es möglich, aus zwölf Streichhölzern ein Polygon herzustellen, dessen Flächeninhalt größer als 9 FE ist? Was ist der größte Flächeninhalt, den ein Polygon, welches man mit 12 Hölzern konstruieren kann, annehmen kann?
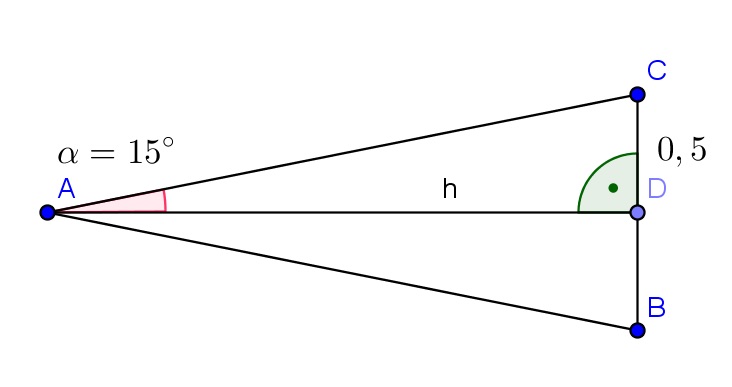
| Ja, es ist möglich, aus zwölf Streichhölzern ein Polygon mit einem Flächeninhalt größer als 9 FE zu konstruieren. Dazu ordnet man die Streichhölzer so an, dass sie die Seiten eines regelmäßigen 12-Ecks darstellen (siehe rechts). |  |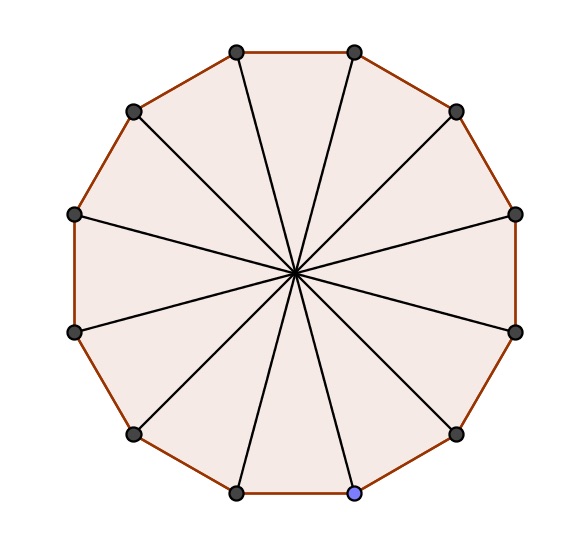
Zur Berechnung des Flächeninhalts dieses 12-Ecks nutzen wir die Unterteilung dieses Polygons in 12 kongruente Dreiecke. Wir betrachten eines dieser Dreiecke.
|
Mit den angegebenen Größen berechnen wir die Höhe h dieses Dreiecks. Es gilt: \(\tan(15°)=\frac{0,5}{h}\Leftrightarrow h=\frac{0,5}{\tan(15°)}\) Folglich gilt für den Flächeninhalt des 12-Ecks: \( 12 \cdot \frac{1}{2} \cdot 1 \frac{0,5}{ \tan(15°)}= \frac{3}{ \tan(15°)}=3( \sqrt 3 +2)=11,2\) |
|
Demnach besitzt das regelmäßige 12-Eck einen Flächeninhalt von 11,2 FE. Es ist davon auszugehen, dass bei einem Umfang von 12 LE, dargestellt durch zwölf Streichhölzer, das regelmäßige 12-Eck die Figur mit dem größten Flächeninhalt ist, da diese der Figur des Kreises am nächsten kommt, die nach der isoperimetrischen Ungleichung der Ebene unter den ebenen Figuren bei konstantem Umfang den größten Flächeninhalt besitzt. Demnach muss der größtmögliche Flächeninhalt etwa 11,2 FE betragen.
Die Aufgabe "Polygone aus Streichhölzern" lässt sich in verschiedenen Jahrgangsstufen im Unterricht einsetzen. Kenntnisse über den Flächeninhalt und den Umfang geradliniger geometrischer Figuren stellen eine Grundvoraussetzung für die Lösung der Aufgabe dar. Diese werden laut LISUM (2015) in der Jahrgangsstufe 5 und 6 (vgl. Kompetenzformulierung 1 (Niveaustufe D)) erlangt. Ein Einsatz der Aufgabe in einer dieser Jahrgangsstufen wäre damit im Rahmen der Unterrichtsthematik "Flächenberechnung bei ebenen geometrischer Figuren" möglich. Eine andere Formulierung der Aufgabenstellung, die dieser Jahrgangsstufe eher angemessen ist (Vermeidung des Begriffs "Polygon", Visualisierungen, Visualisierung des Hinweises (Visualisierung anstelle der Formulierung "überschlagene Polygone"), Verzicht auf Aufgabenteil 4 und andere Kürzungen), ist zu finden in:
Gebel, I., & Kuzle, A. (2016). Geo-Tricks: Ein Problemlösetraining in der Geometrie. MatheWelt - Das Schülerarbeitsheft, 196, 16.
Beim Nachvollzug der Lösungsmöglichkeiten zu Aufgabenteil 4 wird deutlich, dass für die Beantwortung dieser Frage auch Kenntnisse über die Berechnung der Flächen zusammengesetzter Figuren sowie die Berechnung des Flächeninhalts von Dreiecken und Parallelogrammen erforderlich sind. Die Kompetenzformulierungen 2 und 4 (siehe Geförderte Kompetenzen) machen deutlich, dass es sich bei den hier notwendigen Inhalten um Kenntnisse handelt, die sich auf der Niveaustufe E befinden und dass somit erst am Ende der siebten Jahrgangsstufe bei den Schülerinnen und Schülern von diesen Kenntnissen ausgegangen werden kann. Demnach wäre auch ein Einsatz dieser Aufgabe in der Jahrgangsstufe 7 oder 8 (in der hier aufgeführten Formulierung) im Rahmen der Unterrichtsthematik "besondere Punkte und Linien am Kreis" möglich. Die Aufgabenteile 1 bis 3 könnten dabei als Wiederholung dienen und der Aufgabenteil 4 als Vertiefung der behandelten Themen sowie als Verknüpfung der bereits in den vorherigen Jahrgangsstufen erlernten Wissens über den Umfang von Figuren mit dem neu erlernten Wissen über den Flächeninhalt von Dreiecken sowie den Satz des Pythagoras. Die Lösung des Aufgabenteils 5 sollte allerdings auch in diesen Jahrgangsstufen nicht erwartet werden. Da zur Berechnung des Flächeninhalts des regelmäÿigen 12-Ecks, sofern nicht eine vorgegebene Formel verwendet wird, die Höhe eines einzelnen Dreiecks aus dem 12-Eck mithilfe einer trigonometrischen Funktion berechnet werden muss, ist dieser Aufgabenteil frühestens in den Schuljahrgängen 9 und 10 zu bewältigen. Außerdem müssen die Schülerinnen und Schüler bei der Lösung dieser Aufgabe über ein gewisses Wissen hinsichtlich Kreisen und ihren Eigenschaften verfügen, um überhaupt auf die Idee zu kommen, als Figur ein regelmäßiges 12-Eck, welches einem Kreis mit den gegebenen Hilfsmitteln von 12 Streichhölzern am nächsten kommt, als Konstruktion mit der geforderten Eigenschaft vorzuschlagen. Dies wird auch bei Betrachtung der Kompetenzformulierung 6 (siehe Geförderte Kompetenzen) deutlich, die sich auf die Niveaustufe H und demnach auf die zehnte gymnasiale Jahrgangsstufe bezieht.
Damit wird bereits deutlich, dass der Einsatz der gesamten Aufgabe in bestimmten Jahrgangsstufen problematisch sein könnte. Ein generelles Problem dieser Aufgabe könnte darüber hinaus sein, dass die Schülerinnen und Schüler das benötigte Wissen zur Lösung bestimmter Aufgabenteile zwar besitzen, gewisse Aufgabenteile (vor allem die Aufgabenteile 4 und 5) aber nicht lösen können, da sie nicht von selbst auf zielführende Lösungsideen kommen.
Durch die Analyse der Kompetenzformulierungen für die einzelnen Aufgabenteile und den Abgleich mit dem brandenburgischen Rahmenlehrplan Mathematik für die Jahrgangsstufen 1-10 (LISUM, 2015) ergibt sich die folgende Zuordnung:
| Aufgabenteile 1, 2, 3 |
Klasse 5/6, Formulierung der Lösung aber erst in Klasse 7/8 |
| Aufgabenteil 4 | Klasse 7/8 |
| Aufgabenteil 5 | Klasse 9/10 |
Mit der Aufgabe "Polygone aus Streichhölzern" werden insbesondere die Inhaltsbezogenen Kompetenzbereiche [L2] Größen und messen und [L3] Raum und Form sowie die Prozessbezogenen Kompetenzbereiche [K1] Mathematisch argumentieren und [K2] Probleme mathematisch lösen des aus dem brandenburgischen Rahmenlehrplan (Teil C) Mathematik für die Jahrgangsstufen 1-10 (LISUM (2015)), der ab dem Schuljahr 2017/18 gültig ist, gefördert. Da es sich um fünf verschiedene Aufgabenstellungen handelt, werden die einzelnen aufgeführten Kompetenzen durch einige Aufgabenteile mehr gefördert als durch andere.
Inhaltsbezogene Kompetenzformulierungen
Größen und Messen [L2]
Kompetenzformulierung 1 (insbesondere für die Aufgabenteile 1, 2 und 3):
Die Schülerinnen und Schüler stellen Figuren aus einer festgelegten Anzahl an Streichhölzern (hier: 12 Streichhölzer) unter Berücksichtigung eines festgelegten Flächeninhalts (hier: 5 FE, 6 FE, 7 FE und 8 FE) her, indem sie durch Systematisches Ausprobieren Figuren legen und deren Umfang und Flächeninhalt überprüfen.
"näherungsweises Bestimmen von Umfängen und Flächeninhalten [...] z.B. durch Auszählen von Einheitslängen bzw. -flächen" (LISUM, 2015, Größenangaben bestimmen, Niveaustufe D, S.42), "Messen von Größen [insbesondere Längen und Flächeninhalte]" (ebd.)
Erläuterung: Auch wenn einige der zu konstruierenden Polygone keine Rechtecke sind, so reicht es für die Lösung der Aufgabenteile 1, 2 und 3 immerhin aus, solche Polygone so zu erzeugen, dass deren Begrenzungslinien ausschließlich waagerecht und senkrecht sind. Deswegen kann man sich auch die Polygone, die nicht rechteckig sind, als eine Zusammensetzung von Quadraten (Rechenkästchen) zurechtlegen.
Kompetenzformulierung 2 (insbesondere für den Aufgabenteil 4):
Die Schülerinnen und Schüler berechnen den Flächeninhalt und Umfang von rechtwinkligen Dreiecken und Parallelogrammen.
"Berechnen des Umfangs von beliebigen geradlinig begrenzten Figuren" (LISUM, 2016, Größen in Sachzusammenhängen berechnen, Niveaustufe E, S.43), "Berechnen des Flächeninhalts von Dreiecken, Vierecken [...]" (ebd.)
Erläuterung: Um Polygone mit einem Flächeninhalt von <4FE und einem Umfang von nach wie vor 12 Streichhölzern zu legen, müssen weitere ebene geradlinige Figuren wie Dreiecke und Parallelogramme betrachtet werden. Auch beim Legen dieser Figuren muss der Flächeninhalt und der Umfang überprüft werden, um die Frage der Aufgabenstellung 4 zu überprüfen und zu bejahen oder zu verneinen.
Raum und Form [L3]
Kompetenzformulierung 3 (für alle Aufgabenteile):
Die Schülerinnen und Schüler begründen die Lösbarkeit und Lösungsvielfalt von Polygonen mit einem festgelegten Flächeninhalt und Umfang.
"Beschreiben von Lage- und Größenbeziehungen geometrischer Objekte (auch unter Nutzung der Sätze von Thales und Pythagoras)" (LISUM, 2015, Beziehungen zwischen geometrischen Objekten beschreiben, Niveaustufe E, S.50)
Kompetenzformulierung 4 (insbesondere für den Aufgabenteil 4):
Die Schülerinnen und Schüler identifizieren Höhen in Dreiecken, um den Flächeninhalt von Dreiecken berechnen und den Satz des Pythagoras zur Berechnung unbekannter Seiten anwenden zu können.
"Beschreiben besonderer Linien in Dreiecken [...] (z. B. Höhe, [...])" (LISUM, 2015, Geometrische Objekte und ihre Eigenschaften beschreiben, Niveaustufe E, S.48), "Beschreiben von Lage- und Größenbeziehungen geometrischer Objekte (auch unter Nutzung der Sätze von Thales und Pythagoras)" (LISUM, 2015, Beziehungen zwischen geometrischen Objekten beschreiben, Niveaustufe E, S.48)
Kompetenzformulierung 5 (insbesondere für den Aufgabenteil 5):
Die Schülerinnen und Schüler wenden den mathematischen Inhalt der isoperimetrischen Ungleichung der Ebene an, um den Flächeninhalt eines regelmäßigen 12-Ecks als maximalen Flächeninhalts eines Polygons, das mit 12 Streichhölzern gelegt wurde, zu identifizieren.
Kompetenzformulierung 6 (insbesondere für den Aufgabenteil 5):
Die Schülerinnen und Schüler ermitteln unter Zuhilfenahme der trigonometrischen Definitionen (hier der Tangensdefinition) und der Flächeninhaltsformel für Dreiecke den Flächeninhalt eines regelmäßigen n-Ecks (hier 12-Ecks).
"Begründen der Eigenschaften von geometrischen Objekten mithilfe von Symmetrie, einfachen Winkelsätzen, trigonometrischen Beziehungen, dem Satz des Thales und dem Satz des Pythagoras" (LISUM, 2015, Geometrische Objekte und ihre Eigenschaften beschreiben, Niveaustufe H, S.50)
Prozessbezogene Kompetenzformulierungen
Mathematisch argumentieren [K1]
Kompetenzformulierung 7 (für alle Aufgabenteile):
Die Schülerinnen und Schüler begründen ihre Vorgehensweise bei der Lösung der einzelnen Aufgaben mithilfe ihrer mathematischen Kenntnisse über den Umfang und den Flächeninhalt von ebenen geradlinigen geometrischen Figuren (sowie bei Aufgabenteil 5 mithilfe von Kenntnissen über die Kreisfläche und die trigonometrischen Definitionen).
"Begründungen [...] zunehmend selbstständig entwickeln" (LISUM, 2015, S.19)
Probleme mathematisch lösen [K2]
Kompetenzformulierung 8 (für alle Aufgabenteile):
Die Schülerinnen und Schüler nutzen Informative Figuren, um die Fragen beantworten zu können.
"heuristische Hilfsmittel zum Problemlösen anwenden" (LISUM, 2015, S.19)
Heuristische Hilfsmittel:
- Die vorliegende Lösung sollte deutlich gemacht haben, dass die Verwendung von Informativen Figuren ein wichtiges Hilfsmittel zur Lösung der Aufgabe darstellt. Während es hinsichtlich der Aufgabenteile 1 bis 3 durchaus möglich ist, direkt die geforderten Konstruktionen mithilfe von Streichhölzern oder Rechenkästchenpapier zu finden, so hilft eine informative Figur in den Aufgabenteilen 4 und 5 sicherlich bei der Beschreibung geeigneter Konstruktionsverfahren. Vor allem der Aufgabenteil 5 kann durch die Verwendung einer Skizze vereinfacht werden, da auf diese Weise leichter eine Zerlegung des regelmäßigen 12-Ecks in 12 kongruente Dreiecke ersichtlich wird, deren Höhe, die zur Berechnung des Flächeninhalts des regelmäßigen 12-Ecks erforderlich ist, sich wiederum einfacher unter Zuhilfenahme einer Skizze berechnen lässt.
- Gleichungen wurden in dem Lösungsvorschlag vor allem im Rahmen der Aufgabenteile 4 und 5 genutzt, um die Seitenlängen bestimmen zu können.
Heuristische Strategien:
- Eine heuristische Strategie, die in den Aufgabenteilen 1 bis 3 angewendet werden kann, ist das Systematische Probieren. Wenn jemand keine Vorstellung hat, wie er diese Aufgabenteile lösen kann, so wird dieser vermutlich zunächst Versuche nach dem Trial-and-Error-Prinzip unternehmen. Wenn er jedoch erst einmal einige Figuren gefunden hat, die die geforderten Eigenschaften aufweisen, so kann er systematisch durch Verschiebung eines Rechenkästchens in Aufgabenteil 2 oder durch Hinwegnahme eines Rechenkästchens in Aufgabenteil 3 neue Figuren finden.
- Dabei ist die Strategie des Kombinierten Vor- und Rückwärtsarbeitens denkbar.
Heuristische Prinzipien:
- Das Prinzip Zerlegen (und Ergänzen) ist für den Aufgabenteil 5 relevant, da es zur Berechnung des Flächeninhalts des regelmäßigen 12-Ecks sinnvoll erscheint, dieses in 12 kongruente Dreiecke zu zerlegen, wie es in diesem Lösungsvorschlag gezeigt worden ist.
- Das Invarianzprinzip kann beim Aufgabenteil 2 hilfreich sein. Ausgehend von einem gefundenen Polygon, das die geforderten Eigenschaften besitzt, kann eine gewisse Anzahl an Rechenkästchen zunächst fixiert werden, um durch Verschiebung der übrigen Kästchen neue Figuren mit den gewünschten Attributen zu finden.
Da dieser Aufgabe zwischen 3 und 4 Punkten vergeben wurden, wurde diese Aufgabe mit ** gekennzeichnet. Jedoch sind die ersten drei Aufgabenteile für alle Schülerinnen und Schüler geeignet. Hier die Analyse:
Sprachlogische Komplexität:
Die Aufgabe besteht aus einem längeren Text, in dem mehrere Haupt- und Nebensätze auftreten, die sprachliche Rückbezüge aufweisen. Zudem sind in dem Aufgabentext auch sprachliche Ausdrücke wie mehr als zehn oder größer als 9 FE zu finden, die ein aufmerksames Lesen der Aufgabe erforderlich machen. Aus diesen Gründen kann die Aufgabe hinsichtlich der sprachlogischen Komplexität der Stufe 1 zugeordnet werden.
Kognitive Komplexität:
Hinsichtlich der Kognitiven Komplexität kann die Aufgabe auf die Stufe 2 verortet werden, da die Aufgabe mit heuristischen, strategischen und strukturierenden Überlegungen gelöst werden muss.
Formalisierung von Wissen:
Da lediglich zu überlegen ist, wie man die Streichhölzer geeignet darstellen kann, sind keinerlei Formalisierungen zur Lösung der Aufgabe nötig. Deswegen kann die Aufgabe hinsichtlich des Formalisierens von Wissen auf die Stufe 0 eingeschätzt werden.
Formelhandhabung:
Lediglich für die Aufgabenteile 4 und 5 sind einfache Umformungen erforderlich, sodass diese beiden Aufgabenteile der Stufe 1 zuzuordnen sind, während die Aufgabenteile 1 bis 3 keine Formelhandhabung erfordern und deswegen der Stufe 0 zuzuordnen sind.
Stufenzuordnung:
Formalisierung von Wissen
Stufe 0
Formelhandhabung
Stufe 0
Stufe 1
Kognitive Komplexität
Stufe 2
Sprachlogische Komplexität
Stufe 1
Hilfestellungen:
Falls die Schülerinnen und Schüler zu Beginn der Behandlung der Aufgabe Probleme haben, da sie nicht wissen, wie sie an die Aufgabe herangehen und geeignete Polygone finden sollen, könnten die folgenden Hilfestellungen hilfreich sein.
| Allgemein-strategische Hilfen | Inhaltlich-strategische Hilfe | Inhaltliche Hilfe |
| Verdeutliche dir zunächst die Ausgangssituation und die Problemstellung. | Arbeite direkt mit Streichhölzern oder verwende Rechenkästchenpapier, um Polygone zu finden, die die gewünschten Eigenschaften besitzen. | Versuche, das vorgegebene Quadrat zunächst aus den 12 Streichhölzern zu legen und dieses dann durch Umlegen von Streichhölzern auf ein Polygon mit einem Flächeninhalt von 5 FE zu verkleinern. Verwende dann Rechenkästchenpapier, um die gefundenen Polygone festzuhalten und mithilfe des Rechenkästchenpapiers weitere zu finden. |
| Was sollst du in dieser Aufgabe eigentlich tun? | Nimm das erste von dir gefundene und auf dem Rechenkästchenpapier notierte Polygon. Denke dir einige Kästchen fix und "verschiebe" die übrigen, um neue Polygone zu finden. |
Finden die Lernenden kein Polygon mit einem Flächeninhalt von 4 FE oder kleiner (Aufgabenteil 4.), weil sie zu sehr auf das Rechenkästchenpapier fixiert sind und die Polygone so positionieren, dass die Linien stets waagerecht und senkrecht sind, so könnten folgende Hinweise weiterhelfen.
| Allgemein-strategische Hilfen | Inhaltlich-strategische Hilfe | Inhaltliche Hilfe |
| Wie bist du bisher vorgegangen? | Löse dich von dem Rechenkästchengitter. | Versuche mit Dreiecken oder Parallelogrammen zu arbeiten, um neue Polygone zu finden. |
| Warum stößt die vorherige Vorgehensweise an ihre Grenzen? | Suche Polygone, deren Streichhölzer nicht nur auf den Linien des Rechengitters liegen. Welche geometrischen Figuren kennst du, die nicht nur rechte Winkel oder keine rechten Winkel besitzen? |
Sozialformen:
Die Ich-Du-Wir-Methode kann bei dieser Aufgabe gut eingesetzt werden. Vor allem beim Aufgabenteil 2 bietet es sich an, nach einer Einzel- oder Partnerarbeitsphase die Lösungen aller Schülerinnen und Schüler zusammenzutragen, um so möglichst alle Möglichkeiten (für Polygone mit ausschließlich waagerechten und senkrechten Begrenzungslinien) zu finden. Aber auch generell ist dieses Vorgehen geeignet, da jeder zuerst über eigene Strategien oder Ideen nachdenken kann, bevor er sich mit seinem Partner bespricht. Eine abschließende Behandlung der Aufgabe im Plenum kann Lösungsideen oder alternative Lösungsstrategien aufzeigen.
Differenzierungsmöglichkeiten:
- Da sich durch die Analyse der Anforderungen dieser Aufgabe bereits gezeigt hat, dass die Aufgabenteile 1 bis 3, 4 und 5 verschiedenen Kompetenzstufen zuzuordnen sind, kann eine Differenzierung direkt entlang der verschiedenen Aufgabenteile vorgenommen werden. Während die Aufgabenteile 1 bis 3 zumindest abschließend im Plenum mit allen Schülerinnen und Schülern erarbeitet werden können, bietet es sich je nach Klassenstufe an, die Aufgabenteile 4 und 5 nicht, nur teilweise oder nur mit besonders guten Lernenden in einem individuelleren Rahmen zu behandeln.
- Eine weitere Differenzierungsmöglichkeit bietet die Anzahl der Lösungen im Aufgabenteil 2. Man könnte diesen Aufgabenteil für leistungsschwächere Schülerinnen und Schüler dahingehend vereinfachen, dass man ihnen vorgibt, eine gewisse (niedrige) Anzahl an Lösungsmöglichkeiten zu finden, während man für leistungsstärkere Schülerinnen und Schüler entweder eine hohe Anzahl oder keine Anzahl vorgeben könnte. Insbesondere durch die Vermeidung der Angabe einer Anzahl an Lösungen gewinnt die Aufgabe gegenüber einer Angabe zusätzlich an Schwierigkeit, da es unendlich viele Lösungsmöglichkeiten gibt, wenn man sich nicht nur auf diejenigen Polygone beschränkt, deren Linien auf dem Rechenkästchengitter verlaufen.
- Auch durch den Einsatz von Materialien kann die Aufgabe vereinfacht werden. So ist im Rahmen dieser Lösung vor allem für den Aufgabenteil b die Bedeutung des Einsatzes von Rechenkästchenpapier deutlich geworden. Für leistungsschwache Schülerinnen und Schüler wäre es auch denkbar, zunächst direkt mit Streichhölzern zu arbeiten, um die Problemstellung zu verdeutlichen und sie durch den Einsatz des Trial-and-Error-Prinzips zunächst geeignete Polygone finden zu lassen.
Die Aufgabe thematisiert den Zusammenhang zwischen dem Umfang und dem Flächeninhalt von Polygonen. Da aber neben inhaltlichen, vor allem strategische und heuristische Kompetenzen angesprochen werden, geht diese Aufgabe deutlich über den Rahmen einer produktiven Übung hinaus. Demnach ist die Aufgabe als längerfristige Hausaufgabe, als Forschungsprojekt oder eventuell im Rahmen einer Mathe-AG denkbar.
Bearbeitet von: Ana Kuzle, Sandra Pölking (ergänzt von Marisa Pfläging)
Feedback
Wir freuen uns auf Ihre Anregungen und konstruktive Rückmeldung zum Material.
Copyright © 2014-2017 - Ana Kuzle