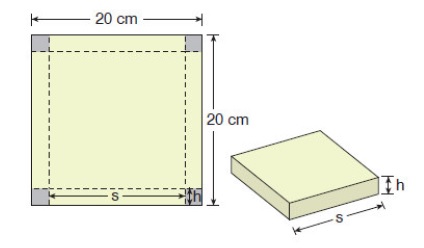
Schachtelproblem
| Klasse | Schulstufe | Thema | Themengebiet | Schwierigkeit |
|---|---|---|---|---|
| 5/ 6 | Primarstufe | Volumenberechnung von Quadern | Größen und Messen, Raum und Form | **, *** |
| Heuristsche Hilfsmittel | Heuristische Prinzipien | Heuristische Strategien |
|---|---|---|
| Informative Figur, Tabelle, Gleichungen | Extremalprinzip | Vorwärtsarbeiten, Systematisches Probieren |
Aufgabenstellung
|
Aus einem quadratischen Blatt Papier mit einer Seitenlänge von 20 cm soll eine oben offene Schachtel mit ganzzahligen Kantenlängen gebaut werden, indem vier gleich große Quadrate an den Ecken aufgeschnitten und die Seitenstücke hochgeklappt werden. Ermittle das Volumen der größtmöglichen Schachtel und gebe die Seitenlänge der Grundfläche dieser Schachtel an.
|
Quellenangabe:
- Lösung
- Themengebiet
- Geförderte Kompetenzen
- Heurismen
- Schwierigkeitsgrad
- Umsetzung im Mathematikunterricht
- Einsatzmöglichkeiten
gegeben:
|
gesucht:
| \({ V }_{ max }\), \({ s }_{ { V }_{ max } }\) |
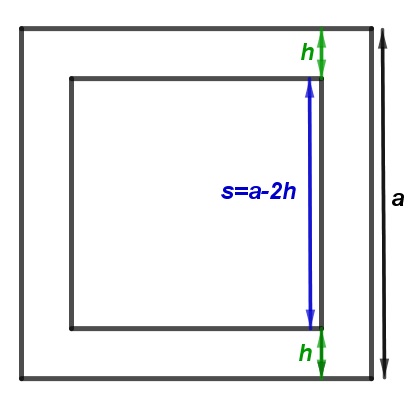
Für \(s\) gilt also:
| Möglichkeit | Seitenlänge s (in cm) | Seitenlänge h (in cm) | Volumen V (in cm³) | Kommentar |
| 1 | 18 | 1 | 324 | |
| 2 | 16 | 2 | 512 | |
| 3 | 14 | 3 | 588 | größtes Volumen |
| 4 | 12 | 4 | 576 | |
| 5 | 10 | 5 | 500 | |
| 6 | 8 | 6 | 384 | |
| 7 | 6 | 7 | 252 | |
| 8 | 4 | 8 | 128 | |
| 9 | 2 | 9 | 36 |
Aus der Tabelle kann \({ V }_{ max }=588cm³\) als maximales Volumen mit der zugehörigen Seitenlänge der Grundfläche \(s=14cm\) entnommen werden.
Alternativ kann auf die Berechnung der Volumina der Möglichkeiten 5 bis 9 verzichtet werden und argumentiert werden, dass das Volumen immer kleiner wird, da \(s²\) von Möglichkeit zu Möglichkeit stärker abfällt als \(h\) ansteigt.
gegeben:
|
gesucht:
| \({ V }_{ max }\), \({ s }_{ { V }_{ max } }\) |
Lösung:
Es werden die verschiedenen möglichen Schachteln aus 20 x 20 cm großen Blättern, so wie in der Aufgabenstellung beschrieben, gebastelt.
 |
 |
Diese werden nun beispielsweise mit Reis gefüllt, da die Papierschachteln Wasser nicht fassen.
Für die Dichte \(\varrho \) eines Stoffes gilt:
|
\(\varrho =\frac { m }{ V } \) \(m\) ... Masse, \(V\) ... Volumen \(\Leftrightarrow \) \(V=\frac { m }{ \varrho } \) |
Die Dichte des Reises ist konstant. Die Schachtel, in die die größte Masse an Reis passt, hat also das größte Volumen.
Die jeweilige Reismenge, die in eine Schachtel passt, wird also abgewogen.
Es ergeben sich folgende Messwerte:
| Möglichkeit |
Seitenlänge s (in cm) |
Seitenlänge h (in cm) | abgewogene Reismasse (in g) | Kommentar |
| 1 | 18 | 1 | 295 | |
| 2 | 16 | 2 | 408 | |
| 3 | 14 | 3 | 511 |
größte Masse \(\Rightarrow \) größtes Volumen |
| 4 | 12 | 4 | 505 | |
| 5 | 10 | 5 | 425 | |
| 6 | 8 | 6 | 353 | |
| 7 | 6 | 7 | 233 | |
| 8 | 4 | 8 | 127 | |
| 9 | 2 | 9 | 30 |
Aus der Messwerttabelle kann \({ m }_{ max }=511g\) mit der zugehörigen Seitenlänge der Grundfläche \(s=14cm\) entnommen werden.
Zu ermitteln ist nun noch das Volumen der Schachtel mit der Grundflächenseitenlänge von 14 cm. Die Reisdichte \({ \varrho }_{ Reis }\) ist allerdings unbekannt. Mit der obigen Formel kann das Volumen also nicht berechnet werden.
Für das Volumen eines Quaders der Kantenlängen \(a\), \(b\) und \(c\) gilt:
\(V=a\cdot b\cdot c\)
Es folgt für diese Schachtel demnach:
\(V=s²\cdot h = (14cm)² \cdot 3cm = 588 cm³\)
Das Volumen der größtmöglichen Schachtel beträgt also \(588 cm²\) und diese Schachtel hat eine Seitenlänge von \(14 cm\).
Hinweise zum zweiten Lösungsweg:
Mit diesem Lösungsweg kann zum Volumen übergeleitet werden. Die Schülerinnen und Schüler haben nur die Massen an Reis abgemessen, die die verschiedenen Schachteln fassen. Es können in diesem Zusammenhang die Fragen in den Raum gestellt werden, wie der Rauminhalt eines Körpers dargestellt werden kann, was die Größe Volumen genau ist und wie diese ermittelt werden kann. Obwohl die Dichte für die meisten Schülerinnen und Schüler der fünften Klasse noch unbekannt ist, können die Lernenden auf die Idee kommen, dass die Schachtel, in die die größte Masse (ugs. Menge/Gewicht des gleichen Stoffes/Gegenstandes) passt, auch das größte Volumen hat. So kann die quantitative Behandlung sowie der Begriff der Dichte umgangen werden und das Volumen nichtsdestotrotz auf diese Art und Weise erarbeitet werden.
Nach dem Aufnehmen der Messwerte könnte im Plenum gemeinsam erarbeitet werden, was das Volumen eines Körpers (hier: Quaders) ist und warum eine Aufgabenlösung durch Abmessen der Masse ungenau ist. So ist der Reis sehr grobkörnig, es können Messfehler u.a. durch die Waage, durch das Verlieren von Reiskörnern beim Messprozess und auch durch das instabile Papier, wodurch bei einer gewissen Reismenge die Form der Schachtel verändert wird, auftreten. Aufgrund des letzteren Aspekts sollte den Schülerinnen und Schülern auch festere Pappe zum Basteln der Schachteln zur Verfügung gestellt werden.
Die Aufgabe "Schachtelproblem" lässt sich bereits in der fünften Klasse im Rahmen der Unterrichtsthematik Volumenberechnung einsetzen. Allerding kann es sein, dass die Schülerinnen und Schüler zu diesem Zeitpunkt noch nicht die Volumenformel für Quader kennen, welche laut LISUM (2015) für die Niveaustufe D (vgl. S.24), also die Jahrgangsstufe 5/6, angesetzt ist. Aber auch ohne Volumenformel kann die Aufgabe gelöst werden (vgl. Lösungsweg 2), die Aufgabe könnte somit auch als Einstieg in die Volumenberechnung von Quadern dienen, indem im Anschluss daran gemeinsam überlegt wird, wie die Aufgabe gelöst werden könnte, ohne zu basteln und abzumessen (vgl. "Lösungsvariante 2"). Ein solcher Einsatz erfordert jedoch eine stärkere Lenkung der Schülerinnen und Schüler (vgl. Abschnitt "Einsatzmöglichkeiten").
Mit der Aufgabe "Schachtelproblem" werden die inhaltsbezogene Kompetenzbereiche [L2] Größen und Messen und [L3] Raum und Form sowie die prozessbezogenen Kompetenzbereiche [K2] Probleme mathematisch lösen und [K6] Mathematisch kommunizieren aus dem brandenburgischen Rahmenlehrplan (Teil C) Mathematik für die Jahrgangsstufen 1-10 (LISUM (2015)), der ab dem Schuljahr 2017/18 gültig ist, gefördert.
Inhaltsbezogene Kompetenzformulierungen
Raum und Form [L3]
Kompetenz 1: Die Schülerinnen und Schüler stellen sich mithilfe einer gegebenen Konstruktionsskizze vor, wie sie eine ensprechende Schachtel basteln können.
"Die Schülerinnen und Schüler können Modelle ausgewählter Körper herstellen [...]" (LISUM (2015), Geometrische Objekte darstellen, Niveaustufe C, S.26)
Erläuterung: Die Aufgabe gibt den Schülerinnen und Schülern eine Abbildung vor, die die gegebenen Informationen darstellt. Diese müssen sie korrekt erfassen können, um die Aufgabe zu verstehen. Dadurch wird deutlich, welche Seitenstücke von dem großen Quadrat hochgeklappt werden (entspricht der Höhe \(h\)) und welche die Seitenlänge \(s\) der Grundfläche ist. Im Weiteren müssen die Lernenden erkennen, welche der Längen sie zur Berechnung des Volumens der Schachtel brauchen. All diese Gegebenheiten müssen sie der Darstellung entnehmen, um zu rechnen und dann das größtmögliche Volumen mit der zugehörigen Seitenlänge anzugeben.
Größen und Messen [L2]
Kompetenz 2: Die Schülerinnen und Schüler nutzen die Größen "Länge" und "Volumen" und die zugehörigen Einheiten "cm" und "cm³" sowie ggf. "dm³" und "Liter".
"Die Schülerinnen und Schüler können die verschiedenen Größen und ihre Einheiten nutzen (auch Flächeninhalt, Volumen [...])" (LISUM (2015), Vorstellungen zu Größen und ihren Einheiten nutzen, Niveaustufe D, S.24)
Erläuterung: Die Aufgabe gibt Längen in cm vor. Die Begriffe Seitenlänge, Grundfläche und Volumen müssen den Schülerinnen und Schülern bekannt sein, damit sie die Aufgabe lösen können. Außerdem ist zu beachten, dass die geforderte Seitenlänge der Grundfläche in cm und das größtmögliche Volumen in cm³ angegeben werden soll, was voraussetzt, dass die Lernenden die verschiedenen Einheiten der Größen kennen und damit sicher umgehen.
Kompetenz 2: Die Schülerinnen und Schüler berechnen Volumina von Quadern.
"Die Schülerinnen und Schüler können Größen messen (auch Volumina [...])", (LISUM (2015), Größenangaben bestimmen, Niveaustufe D, S.24)
Erläuterung: Die Lösung der Aufgabe beinhaltet die Angabe des größtmöglichen Volumens der Schachtel. Dazu müssen die Schülerinnen und Schüler die Formel zur Berechnung des Volumens beherrschen sowie mit der Einheit cm³ arbeiten können. Um die gelernte Formel anzuwenden, müssen sie die benötigte Länge, Breite und Höhe der Schachtel herausfinden. Sind diese Werte gefunden, können die Lernenden sie in die Formel einsetzen und das Volumen errechnen.
Prozessbezogene Kompetenzformulierungen
Probleme mathematisch lösen [K2]
Kompetenz 4: Die Schülerinnen und Schüler nutzen zur Lösung von mathematischen Problemen die Lösungsstrategie des systematischen Ausprobierens.
"Die Schülerinnen und Schüler können Lösungsstrategien (z. B. vom Probieren zum systematischen Probieren) entwickeln und nutzen" (LISUM (2015), S.19)
Erläuterung: Zur Lösung kann nicht durch reines Nachdenken gelangt werden, sondern durch Finden verschiedener Werte, die in die Volumenformel eingesetzt werden oder mithilfe derer verschiedene Modelle hergestellt werden und das Volumen abgemessen wird. Die so erhaltenen Volumina werden anschließend verglichen, damit der größten Wert gefunden wird. Hierzu werden systematisch verschiedene Werte probiert und mit ihnen das Volumen errechnet, bzw. es werden verschiedene Modelle hergestellt und mit diesen wird das Volumen abgemessen. Aus dem Probieren wird dabei ein systematisches Probieren, weil mit einem Wert gestartet wird, der schrittweise vergrößert/verkleinert wird und dabei die Entwicklung des Volumens beobachtet wird. So kann erkannt werden, dass das Volumen bei einer bestimmten Seitenlänge am größten ist. Wird zur Überprüfung mit der nächsten Zahl weiter gerechnet, nimmt es wieder ab. Somit führt das systematische Probieren zur Lösung der Aufgabe.
Kompetenz 5: Die Schülerinnen und Schüler wenden zum Problemlösen die heuristischen Hilfsmittel der Tabelle und der informativen Figur (, ggf. auch der Gleichungen) an.
"Die Schülerinnen und Schüler können heuristische Hilfsmittel zum Problemlösen anwenden" (LISUM (2015), S.19)
Erläuterung: Beim Schachtelproblem bietet es sich an, die Lösungen in einer Tabelle festzuhalten und/oder eine informative Figur zum besseren Verständnis und zur Anschaulichkeit zu nutzen. Bei einer Tabelle können die verschiedenen Versuche mit verschiedenen Zahlen in übersichtlicher Form notiert werden. Es lässt sich damit gut erkennen, welche Werte schon in die Formel eingesetzt wurden und wie sich das Volumen entwickelt hat. Mithilfe einer informativen Figur, die die Aufgabe auch schon vorgibt, können sich die gegebenen Werte besser vorgestellt werden und anhand dieser kann verstanden werden, was gefordert ist. Werden die veränderten Seitenlängen in die informative Figur eingetragen, ist es einfacher zu erkennen, welchen Wert die Höhe annimmt. So wird das Finden der Werte zum Einsetzen in die Volumenformel erleichtert.
Mathematisch kommunizieren [K6]
Kompetenz 6: Die Schülerinnen und Schüler dokumentieren die eigenen Problembearbeitungen nachvollziebar.
"Die Schülerinnen und Schüler eigene Problembearbeitungen und Einsichten dokumentieren und darstellen" (LISUM (2015), S.21)
Erläuterung: Die Aufgabe ist kaum im Kopf zu lösen, da zunächst die möglichen Seitenlängen einer Schachtel ermittelt werden müssen, mithilfe derer dann das jeweilige Volumen berechnet werden kann. Es ist somit unumgänglich die Herangehensweise festzuhalten, um die verschiedenen Schritte zu verstehen. Dies ist sowohl während der Bearbeitung wichtig, da dann erkannt werden kann, mit welchen Werten schon gerechnet wurde, als auch danach, um Fehler erkennen und berichtigen zu können.
- Die gegebene Zeichnung wird bei der Lösung übernommen und somit wird eine informative Figur angefertigt, die sich die Schülerinnen und Schüler verständlich anpassen können. Anhand der Zeichnung können sie sich besser vorstellen, welchen Wert die Höhe annimmt, wenn eine Seitenlänge festgelegt ist. So kann die informative Figur dazu beitragen, dass sich die Lernenden richtige Werte zum Einsetzen in die Volumenformel überlegen.
- Daneben wird eine Tabelle genutzt, in welche die verschiedenen Seitenlängen und Höhen eingetragen und in welcher die daraus entstehenden Volumina berechnet werden. Mithilfe der Tabelle kann der Lösungsweg in übersichtlicher Form festgehalten werden und es ist ersichtlich, welche Werte schon durchgerechnet worden sind und welche noch nicht. Die Volumina der verschiedenen Schachteln können in der Tabelle sehr gut miteinander vergleichen und das größte erkannt werden.
- Um die verschiedenen Möglichkeiten für die Seitenlängen zu ermitteln wird beim ersten Lösungsweg eine Gleichung für s aufgestellt. Darüber hinaus wir das Volumen der jeweiligen Schachtel mit der Volumenformel für Quader ermittelt. Somit werden auch Gleichungen als Heuristische Hilfsmittel verwendet.
- Bei der Lösung der Aufgabe wird zunächst das Gegebene angeschaut und überlegt wie die gegebenen Informationen genutzt werden können. Es wird sich auch überlegt, wie genau vorgegangen wird. Somit handelt es sich um Vorwärtsarbeiten.
- Während der Bearbeitungen wird die Strategie des systematischen Probierens genutzt, da mit einem Wert der Seitenlänge angefangen wird, die zugehörige Höhe anhand der informativen Figur bestimmt und beide nach und nach verändert werden, sodass das Volumen immer größer wird.
- Nach dem Extremalprinzip wird versucht die Werte so zu wählen, dass ein maximales Volumen herauskommt. Die Seitenlänge der Grundfläche und die Höhe werden so verändert, dass das Volumen immer größer wird bis das Maximum erreicht ist.
In Anbetracht des Einsatzes der Aufgabe in einer fünften Klasse hat das Schachtelproblem nach Cohors-Fresenborg et al. bezüglich des ersten Lösungsweges einen Schwierigkeitsgrad von *** und bezüglich der zweiten Lösungsvariante von **.
Die Sprachlogische Komplexität des Schachtelproblems lässt sich auf Stufe 2 anordnen, da die Reihenfolge der Sätze nicht der Reihenfolge der Schritte bei der mathematischen Bearbeitung entspricht und die im Text enthaltenen Informationen nicht unmittelbar für die mathematische Bearbeitung zu entnehmen sind.
Vor der Bearbeitung der Aufgabe muss genau überlegt werden, wie bei der Lösung vorgegangen wird. Um den Rechenaufwand gering zu halten, sollte außerdem zusätzlich überlegt werden, wie argumentiert werden kann, dass ab einer bestimmten Schachtel das Volumen immer kleiner wird. Somit lässt sich die Kognitive Komplexität der Aufgabe ebenfalls auf Stufe 2 ansiedeln.
Die Formalisierung von Wissen entspricht der Stufe 1, da lediglich die Volumenformel für Quader zu erstellen ist und beim rechnerischen Lösungsweg eine Formel für die Seitenlänge \(s\) der Grundfläche mithilfe der gegebenen Abbildung erstellt werden muss, damit die möglichen Seitenlängen einer Schachtel ermittelt werden können.
Um die möglichen Kantenlängen einer Schachtel zu ermitteln, wird beim ersten Lösungsweg aus der gegebenen Skizze eine Gleichung für die Seitenlänge \(s\) aufgestellt. Bezüglich dieses Lösungsweges lässt sich die Formelhandhabung auf Stufe 1 anordnen. Beim zweiten Lösungsweg wird dieser Schritt umgangen, indem alle möglichen Schachteln, auf die in der Aufgabenstllung beschriebene Art und Weise gebastelt werden. Wenn nicht mit der Formel für die Dichte argumentiert wird, lässt sich die Formelhandhabung der Aufgabe bezüglich dieses Lösungsweges auf Stufe 0 ansiedeln, anderenfalls ebenso auf Stufe 1.
Bei der Bearbeitung des Schachtelproblems kann den Schülerinnen und Schülern an einigen Stellen Schwierigkeiten bereiten. Zwei solcher kritischer Stellen werden im Folgenden genannt und es wird dargestellt mit welchen allgemein-strategischen Hilfen, inhaltsorientierten strategischen Hilfen und inhaltlichen Hilfen als Lehrperson darauf eingegangen werden kann.
Die Schülerinnen und Schüler können gleich zu Beginn des Lösungsfindungsprozesses das Problem haben, dass sie nicht auf die Idee kommen, die Aufgabe durch systematisches Probieren zu lösen. Tritt diese Schwierigkeit auf, so können den Schülerinnen und Schülern folgende Hilfen gegeben werden.
| Allgemeine strategische Hilfen | Inhaltsorientierte strategische Hilfen | Inhaltliche Hilfen |
| Was ist gegeben und gesucht? | Welche Hilfsmittel kannst du verwenden? | Welche Möglichkeiten gibt es für Schachteln, die aus dem 20 x 20 cm großen Blatt gebastelt werden können? |
| Welche Formen und Körper sind hier relevant? Was weißt du bereits über diese? | Vielleicht hilft es dir, wenn du eine Tabelle anlegst. | Wie kannst du das Volumen einer Schachtel berechnen? |
| Überlege dir, wie du am Ende überprüfen kannst, ob dein Ergebnis richtig ist! | Kannst du eine bekannte Berechnungsformel für eine Eigenschaft eines Quaders anwenden? | Was weißt du über Quader? |
Eine weitere Schwierigkeit kann darin bestehen, ab einer bestimmten Schachtelmöglichkeit mit der Volumenformel für Quader und den in dieser enthaltenen Faktoren zu argumentieren, dass alle weiteren Schachteln ein kleineres Volumen haben (\(s²\) fällt von Möglichkeit zu Möglichkeit stärker ab, als \(h\) ansteigt). In diesem Fall können den Lernenden folgende Hinweise weiterhelfen.
| Allgemeine strategische Hilfen | Inhaltsorientierte strategische Hilfen | Inhaltliche Hilfen |
| Halte den Rechenaufwand so gering wie möglich! | Musst du wirklich alle Volumina berechnen? | Was fällt dir beim Einsetzen der Kantenlängen in die Volumenformel auf? |
| Du kannst auch mit bekannten Gleichungen und mit Variablen, die in diesen enthalten sind, argumentieren. | Wird das Volumen ab einer bestimmten Seitenlänge s immer kleiner oder größer? | Wie verhält sich \(s²\) im Vergleich zu \(h\), wenn du einen größeren Wert für \(s\) einsetzt? |
- Frontalunterricht mit Anteilen an Einzelarbeit/Partnerarbeit (insbesondere bei der Verwendung als Einstieg in die Thematik Volumenberechnung von Quadern)
- Partnerarbeit
- Einzelarbeit
Sowohl für leistungsschwächere als auch für leistungsstärkere Schülerinnen und Schüler ist eine Differenzierung möglich.
Für leistungsschwächere Schülerinnen und Schüler könnten folgende Differenzierungsmaßnahmen ergriffen werden:
- Es könnte der Hinweis gegeben werden, dass die Höhe nicht die Summe der beiden hochgeklappten Seitenstücke ist, sondern nur eine Länge davon. Wenn sie die Seitenlänge 12 cm wählen und diese von 20 cm abziehen, bleiben als Seitenstücke noch 8 cm übrig. In der Formel zur Berechnung des Volumens ist aber nicht 8 cm die Höhe, sondern 4 cm, da die Seitenstücke einzeln hochgeklappt werden, sodass der Rand an allen Seiten 4 cm ausmacht (h=(20cm-Seitenlänge):2).
- Den Lernenden, die die Volumenberechnung noch nicht komplett verinnerlicht haben, könnte die Formel für die Volumenberechnung vorgeben werden.
- Es kann den Schülerinnen und Schülern ein 20 x 20 cm großes Blatt Papier gegeben werden, sodass sie sich eine bessere Vorstellung davon machen können, wie eine solche Schachtel hergestellt werden kann und dies haptisch nachvollziehen können.
|
Beispiel: Möglichkeit 4
|
|
|
|
|
|
Beispiel: Möglichkeit 8
|
|
|
|
|
Für leistungsstärkere Schülerinnen und Schüler könnte die Aufgabe auf folgende Weise verändert werden:
- In der gegebenen Skizze könnten die Angaben weggelassen werden oder die Skizze könnte sogar komplett weggelassen werden. Die Schülerinnen und Schüler müssten die Skizze dann selbstständig anhand des Textes beschriften, bzw. erstellen.
- Es könnte zusätzlich die Aufgabe gestellt werden, dass die Schülerinnen und Schüler mehrere verschiedene Lösungsmöglichkeiten finden.
Da in dieser Aufgabe ein Volumen berechnet werden muss und dies erst ab der fünften Klasse behandelt wird, eignet sich diese Aufgabe nur bedingt zum Einstieg in das Thema. In einem solchen Fall ist eine stärkere Lenkung durch die Lehrperson erforderlich, damit die Schülerinnen und Schüler zunächst auf den zweiten Lösungsweg gelangen. Es könnte mit den Lernenden gemeinsam erarbeitet werden, welche Möglichkeiten es für die Seitenlängen einer solchen Box gibt. Außerdem könnten im Plenum vor dem Abmessen in Form von Klassenabstimmungen Vermutungen generiert werden, in welche Box wohl am meisten Reis hineinpasst. Somit würden alle Schülerinnen und Schüler angesprochen und für den folgenden Unterricht aktiviert werden. Die Gleichung für die Dichte ist den Lernenden zu Beginn der fünften Klasse noch nicht bekannt, deshalb müsste auf diese verzichtet werden und es kann erst einmal nur mit der Masse argumentiert werden. Den Schülerinnen und Schülern könnte dann Papier zur Verfügung gestellt werden, sodass sie (arbeitsteilig) die verschiedenen Boxen basteln und mit diesen messen, wieviel Reis damit jeweils abgefüllt werden kann. Im Anschluss daran könnten die verschiedenen Messwerte festgehalten werden und jeder kann für sich herausfinden, ob er mit seiner Vermutung richtig lag. Die Aufgabe kann somit gemeinsam beantwortet werden. Im weiteren Unterricht könnte dann thematisiert werden, wie der Inhalt der Schachtel genau ermittelt werden kann und es kann zur Größe des Volumens und deren Einheit hingeleitet werden. Bei diesem Einsatz der Aufgabe wird allerdings das eigenständige Problemlösen der Schülerinnen und Schüler weniger gefördert, da die Vorgehensweise für die Bearbeitung der Aufgabe bereits durch das lehrergelenkte LehrerInnen-SchülerInnen-Gespräch vorgegeben wird. Müssten die Schülerinnen und Schüler die Aufgabe ohne das Wissen über die Volumenberechnung eigenständig lösen, so würden sie die Motivation verlieren, da sie die Aufgabe nicht lösen können. Es bestünde allerdings die Möglichkeit die Aufgabe wie oben beschrieben am Anfang der Unterrichtseinheit vorzustellen, die Aufgabe gemeinsam nachzuvollziehen und die Lernenden Lösungsideen entwickeln zu lassen. Es würde klar werden, dass man zur Lösung ein Volumen berechnen muss, worauf man in der folgenden Stunde näher eingeht. Am Ende der Unterrichtseinheit könnte man auf die Aufgabe zurückkommen und sie könnte mit dem nötigen Wissen gelöst werden.
Darüber hinaus eignet sich die Aufgabe aber insbesondere auch zur vertiefenden Übung mit einem forschenden Charakter. Erst wenn schon Wissen über die Volumenberechnung vorhanden ist, sollte diese Aufgabe als Übung vorgestellt werden. Die Schülerinnen und Schüler können sich dann auf das Verstehen der Aufgabe konzentrieren und überlegen, wie sie diese lösen könnten. Dabei wählen sie selbst den Lösungsweg, der ihnen am vorteilhaftesten erscheint. Sie erforschen, wie sich das Volumen durch die Veränderung der Werte vergrößert oder verkleinert und wann das Maximum erreicht ist.
Bearbeitet von: Marie Ecknig, Lydia Schneider (ergänzt von Marisa Pfläging)
Feedback
Wir freuen uns auf Ihre Anregungen und konstruktive Rückmeldung zum Material.
Copyright © 2014-2017 - Ana Kuzle