Email : info(at)proffi-m.de
Feedback und Fragen

Stehaufmännchen

Fehlermeldung

Deprecated function: The each() function is deprecated. This message will be suppressed on further calls in FieldCollectionItemEntity->fetchHostDetails() (Zeile 313 von /www/htdocs/w0127817/beta.proffi-m.de/sites/all/modules/field_collection/field_collection.entity.inc).

Klasse	Schulstufe	Thema	Themengebiet	Schwierigkeit
9/ 10	Sekundarstufe I	Volumen von zusammengesetzten Körpern berechnen	Funktionaler Zusammenhang, Raum und Form	**

Heuristsche Hilfsmittel	Heuristische Prinzipien	Heuristische Strategien
Informative Figur, Gleichungen	Zerlegungs- und Ergänzungsprinzip	Vorwärtsarbeiten

Aufgabenstellung

Ein Stehaufmännchen hat einen Durchmesser von 10 cm. Damit das Stehaufmännchen funktioniert, müssen die beiden Teilkörper gleich schwer sein. Wie hoch darf der obere Teilkörper höchstens sein, wenn das Stehaufmännchen noch funktionieren soll?

Quellenangabe:

in Anlehnung an http://fontaneum.de/Downloadcenter/Mathematik/Lernwerkstatt/Lernwerkstatt%20Kegel.pdf

Lösungsvariante 1

Zusammenhang zwischen Volumen, Masse und Dichte:

\(\\ \rho =\frac { m }{ V } \)

Diese Gleichung wird nach der Masse umgestellt.

\(\rho \quad =\quad \frac { m }{ V } \) \( |\cdot V\)

\(\rho \cdot V\quad =\quad m\\ \)

Damit das Stehaufmännchen noch funktioniert müssen die beiden Körper (der Kegel und die Halbkugel) gleich schwer sein. Die beiden Massen der Körper werden jetzt gleichgesetzt. Um die Höhe zu berechnen, muss die Gleichung nach der Höhe umgeformt werden.

\({ m }_{ Halbkugel }\quad =\quad { m }_{ Kegel }\)

\(\rho \cdot { V }_{ Halbkugel }\quad =\quad \rho \cdot { V }_{ Kegel }\)

\(\\ \rho \cdot \frac { 2 }{ 3 } \cdot \pi \cdot { r }^{ 3 }\quad =\quad \rho \cdot \frac { 1 }{ 3 } \cdot \pi \cdot { r }^{ 2 }\cdot h\qquad |\div \rho \)

\(\frac { 2 }{ 3 } \cdot \pi \cdot { r }^{ 3 }\quad =\quad \frac { 1 }{ 3 } \cdot \pi \cdot { r }^{ 2 }\cdot h\qquad |\cdot 3\)

\(2\cdot \pi \cdot { r }^{ 3 }\quad =\quad \pi \cdot { r }^{ 2 }\cdot h\)

Da der Körper einen Durchmesser von 10 cm hat, muss fürden Radius der Halbkugel 5 cm eingesetzt werden.

\(2\cdot \pi \cdot { (5cm) }^{ 3 }\quad =\quad \pi \cdot { (5cm) }^{ 2 }\cdot h\)

\(2\cdot \pi \cdot 125{ cm }^{ 3 }\quad =\quad \pi \cdot 25{ cm }^{ 3 }\cdot h\qquad |\div \pi \)

\(2\cdot 125{ cm }^{ 3 }\quad =\quad 25{ cm }^{ 2 }\cdot h\qquad |\div 25{ cm }^{ 2 }\)

\(2\cdot 5cm\quad =\quad h\qquad \)

\(10cm\quad =\quad h\qquad \)

Damit das Stehaufmännchen noch funktionert, darf der Kegel maximal 10cm hoch sein.

Lösungsvariante 2

Das Volumen eines Körpers lässt sich auch als eine Funktion in Abhängigkeit von der Höhe darstellen. Wir erhalten folgende Gleichungen für die beiden Körper:

\(f\left( h \right) =\quad \frac { 1 }{ 3 } \cdot \pi \cdot { r }^{ 2 }\cdot h\) für den Kegel und

\(f\left( h \right) =\quad \frac { 2 }{ 3 } \cdot \pi \cdot { r }^{ 3 }\) für die Halbkugel

Die Masse der beiden Körper ist gleich, wenn die beiden Gleichungen einen Schnittpunkt besitzen. Die Gleichungen werden zunächst gleichgesetzt.

\(\frac { 1 }{ 3 } \cdot \pi \cdot { r }^{ 2 }\cdot h\quad =\quad \frac { 2 }{ 3 } \cdot \pi \cdot { r }^{ 3 }\quad \)

Diese Gleichung wird jetzt nach der Höhe aufgelöst.

\(\frac { 1 }{ 3 } \cdot \pi \cdot { r }^{ 2 }\cdot h\quad =\quad \frac { 2 }{ 3 } \cdot \pi \cdot { r }^{ 3 }\qquad |\div \pi \)

\(\frac { 1 }{ 3 } \cdot { r }^{ 2 }\cdot h\quad =\quad \frac { 2 }{ 3 } \cdot { r }^{ 3 }\qquad |\cdot 3\)

\({ r }^{ 2 }\cdot h\quad =\quad 2\cdot { r }^{ 3 }\qquad |\div { r }^{ 2 }\)

\(h\quad =\quad 2\cdot r\qquad \)

Jetzt muss man nur noch für den Radius der Halbkugel 5cm einsetzten und erhält als Ergebnis eine Höhe h von 10cm. Somit beträgt die Maximalhöhe des Kegels 10cm.

Die Stehaufmännchen-Aufgabe soll in der Unterrichtseinheit Körperberechnung thematisiert werden, welche an brandenburgischen Gymnasien in der neunten Klasse unterrichtet wird. In dieser sollen laut Rahmenlehrplan Kompetenzen der Nivaustufe G erlangt werden, was bei der Aufgabe "Stehaufmännchen" der Fall ist (vgl. Abschnitt "Geförderte Kompetenzen").

Die Schülerinnen und Schüler haben im Physikunterricht in der Doppeljahrgangsstufe 7/8 (vgl. brandenburgischer "Rahmenlehrplan. Teil C. Physik Jahrgangstufen 7-10.", S.29) das thermische Verhalten von Körpern behandelt und dabei den "Zusammenhang zwischen Masse und Volumen" (ebd. S.30) und die "Dichte als physikalische Größe" (ebd.) kennen gelernt. Dieses Wissen wird für die Lösungsvariante 1 der Aufgabe benötigt. Somit ermöglicht die Stehaufmännchen-Aufgabe einen fächerübergreifenden Unterricht.

Vor dem Bearbeiten der Aufgabe im Unterricht sollte jeweils die allgemeine Volumenformel für Kegel und Kugeln erarbeitet worden sein. Erst danach kann die Aufgabe von den Schülerinnen und Schülern bearbeitet werden. Außerdem haben die Lernenden laut Rahmenlehrplan in der achten Klasse gelernt, Gleichungen zu lösen (vgl. Rahmenlehrplan, S.18, Nivaustufe F). Auch dieses Wissen ist für die Lösung der Aufgabe notwendig. In der neunten Klasse lernen die Schülerinnen und Schüler "Eigenschaften von Funktionen" zu beschreiben (ebd. S.29). Lösungsvariante 2 tritt also wahrscheinlich eher auf, wenn die Unterrichtseinheit Körperberechnung in der neunten Klasse zeitlich nach dem Thema der Analysis erfolgt.

Somit dient die Stehaufmännchen-Aufgabe der produktiven Übung und der Festigung von neu erlernten Zusammenhängen, wobei die Schülerinnen und Schüler bereits bekannte Zusammenhänge, sowie Vorgehensweisen zur Lösung einer Gleichung anwenden müssen.

Inhaltsbezogene Kompetenzen

Bezüglich der Leitidee Größen und Messen werden folgende Inhalte gefordert:

Die Schülerinnen und Schüler kennen die Volumenformel für Kegel und Kugel.

Größen und Messen, Niveaustufe G „Die Schülerinnen und Schüler können Größenangaben messen und Maße aus den Darstellungen entnehmen“ (RLP, S.24); Rechnen mit Größen, Niveaustufe G „Die Schülerinnen und Schüler können mit Größenangaben rechnen (auch bei [...] Kegeln und Kugeln sowie zusammengesetzten Körpern[...])“ (ebd., S.25)

Um die Aufgabe lösen zu können, muss der Körper in Teilkörper zerlegt werden. Aus der Leitidee Raum und Form werden die folgenden Kompetenzen gefordert:

Die Schülerinnen und Schüler können Körper in Teilkörper zerlegen.

Raum und Form, Niveaustufe G „Die Schülerinnen und Schüler können geometrische Objekte beschreiben (auch Differenz- und Teilkörper sowie Differenz- und Teilflächen)“ (RLP, S.26)

Im Lösungsweg 2 wird auf den Umgang mit Termen zurückgegriffen. Hierbei sollen die Schülerinnen und Schüler nach der Leitidee Gleichungen und Funktionen folgende Kompetenzen erwerben:

Die Schülerinnen und Schüler können eine Gleichung für das Volumen der Teilkörper in Abhängigkeit von der Höhe aufstellen.

Gleichungen und Funktionen, Niveaustufe E „Die Schülerinnen und Schüler können Terme und Gleichungen darstellen (auch im Bereich der rationalen Zahlen)“ (RLP, S.28)

Prozessbezogene Kompetenzen

Für die Lösung der Aufgabe sind prozessbezogene Standards relevant. Sowohl das mathematische Probleme lösen als auch das mathematische Modellieren werden mit dieser Aufgabe abgedeckt.

Folgendes wird beim mathematischen Problemlösen gefordert:

Die Schülerinnen und Schüler lösen eine Aufgabe die ihnen unbekannt ist.

Probleme mathemathisch lösen, „Die Schülerinnen und Schüler können Aufgaben bearbeiten, zu denen sie noch keine Routinestrategie haben (sich zu helfen wissen)“) (RLP, S.19); "Die Schülerinnen und Schüler können Kenntnisse, Fähigkeiten und Fertigkeiten bei der Bearbeitung von Problemen anwenden" (ebd.).

Da in der Aufgabe ein unbekannter zusammengesetzter Körper berechnet werden muss, haben die Schülerinnen und Schüler keine allgemeine Lösungsstrategie. Durch diese Aufgabe soll eine solche aber entwickelt werden. Haben die Lernenden eine Idee für die Lösung, müssen sie in diesem Fall den Körper in Teilkörper zerlegen und das Volumen berechnen.

Die Schülerinnen und Schüler entwickeln eine Strategie zum Lösen der Aufgabe (z.B. durch kombiniertes Vorwärts- und Rückwärtsarbeiten, Analogieschlüsse oder Rückführung von Unbekanntem auf Bekanntes), dabei benutzen sie bekannte heuristische Hilfsmittel (Skizze, Figur, Gleichungen) unter Verwendung heuristscher Prinzipen.

Probleme mathematisch lösen, „Die Schülerinnen und Schüler können Lösungsstrategien (z.B. vom Probieren zum systematischen Probieren) entwickeln und nutzen“, „Die SuS können heuristische Hilfsmittel zum Problemlösen anwenden.“ (RLP, S.19)

Beim matheamtischen Modellieren wird folgendes gefordert:

Die Schülerinnen und Schüler können anhand der Zeichnung und dem Aufgabentext die notwendigen Informationen verwenden.

Mathematisch Modellieren, „Die Schülerinnen und Schüler können relevante Informationen aus Sachtexten und anderen Darstellungen entnehmen“ (RLP, S.20)

Aus dem Kompetenzbereich mit symbolischen, formalen, technischen Elementen der Mathematik umgehen wird folgender Bereich gefordert:

Die Schülerinnen und Schüler verwenden die Volumenformel in Abhängigkeit von der Höhe des Körpers. Sie stellen mit dieser Volumenformel eine Gleichung auf und berechnen jeweils den Zusammenhang zwischen Höhe und Radius des Körpers.

Mit symbolischen, formalen, technischen Elementen der Mathematik umgehen, „Die Schülerinnen und Schüler können Tabellen, Terme, Gleichungen und Diagramme zur Beschreibung von Sachverhalten nutzen“, „Die Schülerinnen und Schüler können Variablen und Funktionen zur Bearbeitung von Aufgaben nutzen.“ (RLP, S.20)

Heuristische Hilfsmittel:

Das Stehaufmännchen wird den Schülerinnen und Schülern mittels einer informativen Figur vorgelegt. Das Stehaufmännchen besteht aus einer Halbkugel und einem Kegel. Diese beiden Teilkörper sind durch die Figur gegeben und müssen von den SuS erkannt werden. Aufgrund der Figur sehen die Schülerinnen und Schüler, dass es sich um zwei unterschiedliche Figuren handelt, die durch eine Gleichung in einen Zusammenhang gebracht werden müssen.

Außerdem werden Gleichungen benutzt, um das Volumen in Abhängigkeit von der Höhe darzustellen. Mithilfe der beiden Gleichungen für das Volumen der beiden Teilkörper kann der Schnittpunkt der Gleichungen ermittelt werden. Für diesen Schnittpunkt sind die Volumina der beiden Körper in Abhängigkeit von der Höhe und damit auch die Volumina gleich.

Heuristische Strategien:

Bei dieser Aufgabe ist das Vorwärtsarbeiten von Bedeutung:

Gegeben ist ein Stehaufmännchen. Ausgehend davon versucht man die Lösung zu erarbeiten. Die Lernenden müssen sich überlegen, welchen Zusammenhang es zwischen Masse und Volumen von Körpern gibt und auf die Formel für die Dichte kommen. Das Volumen muss jetzt für die beiden Teilkörper berechnet und gleichgesetzt werden, da die Teilkörper sowohl die gleiche Masse als auch eine gleiche Dichte besitzen. Dann wird nach der Höhe umgeformt.

Heuristische Prinzipien:

Für die Lösung der Aufgabe ist das heuristische Prinzip Zerlegen und Ergänzen notwendig.

Das Zerlegen besitzt bei dieser Aufgabe die wichtigste Stellung, denn ohne den Körper zu zerlegen, wird es sehr schwierig das Volumen des Körpers zu bestimmen. Durch die Zerlegung in zwei Teilkörper kann man das Volumen für die beiden Teile bestimmen und gleichsetzen (vgl. Lösungsvariante 1).

Insgesamt ergeben sich sowohl für die erste Lösungsvariante als auch für den zweiten Lösungsweg 4 Punkte. Nach Cohors-Fresenborg et al hat die Stehaufmännchen-Aufgabe damit einen Schwierigkeitsgrad von **.

Sprachlogische Komplexität:

Die Aufgabenstellung besteht aus drei Hauptsätzen. Zunächst wird die Größe des Durchmessers gegeben, der für den ersten Schritt des Lösungsweges 1 unrelevant ist. Dem folgenden Satz kann dann entnommen werden, dass die Massen der Halbkugel und des Körpers gleichgesetzt werden müssen. Und mit der Frage nach der Höhe wird dann darauf hingewiesen die Volumenformeln für Halbkugel und Kegel und die anfangs gegebene Größe des Durchmessers zu verwenden, wobei aus diesem zunächst der Radius ermittelt werden muss. Es lässt sich also erkennen, dass die Reihenfolge der letzten beiden Sätze den Schritten der mathematischen Bearbeitung entspricht, wobei beim letzten Bearbeitungsschritt auf die Information aus dem ersten Satz zurückgegriffen wird. Da es sich beim ersten Satz aber nur um eine einzige Information handelt und es sich um kurze präzise Sätze handelt, kann die Sprachlogische Komplexität für Lösungsvariante 1 bezüglich der Sprachlogischen Komplexität der Stufe 0 zugeordnet werden. Auch bezüglich der Lösungsvarainte 2 hat die Aufgabe eine Sprachlogische Komplexität der Stufe 0, da bei dieser Lösungsvariante von der Schlussfrage ausgegangen wird und dann beim Gleichsetzen und Umformen die vorher gegebenen Informationen benutzt werden.

Kognitive Komplexität:

Die Kognitive Komplexität entspricht für beide Lösungswege der Stufe 1, da wie unter dem Aspekt der "Sprachlogischen Komplexität" bereits beschrieben ist, Denkvorgänge nacheinander oder auch parallel abzuarbeiten sind. Außerdem ist kein Hinweis auf die Formel für die Dichte von Stoffen gegeben und die Schülerinnen und Schüler müssen die Nebenbedingung erkennen, dass die Halbkugel und der Kegel aus dem gleichen Material bestehen und somit auch die gleiche Dichte haben. Erst daraus kann mit der Information über die gleichen Massen der Körper gefolgert werden, dass die Volumina ebenfalls gleichgroß sein müssen, damit das Stehaufmännchen noch funktioniert.

Formalisierung von Wissen:

Bei beiden Lösungswegen müssen die Schülerinnen und Schüler die Formel für die Dichte eigenständig erbringen und verstehen: Bei Lösungsweg 1 um die beiden Volumina gleichsetzten zu können und bei Lösungsvariante 2 um die Funktionen gleichzusetzen. Außerdem müssen die Lernenden für die Berechnung der Höhe die Volumenformeln für Kegel und Kugel verwenden (bzw. die für die Halbkugel aufstellen) und gleichsetzen. Somit hat die Aufgabe bezüglich der Formalisierung von Wissen einen Schwierigkeitsgrad der Stufe 2.

Formelhandhabung:

Der erste Lösungsweg beinhaltet nur einfache Termumformungen und wenige Schritte. Im zweiten Lösungsweg werden zwei Terme gleichgesetzt um den Schnittpunkt zu bestimmen. Diese Gleichung wird in wenigen einfachen Schritten gelöst. Deshalb wird die Aufgabe hinsichtlich der Formalhandhabung der Stufe 1 zugeordnet.

Stufenzuordnung:

Formalisierung von Wissen

Stufe 2

Formelhandhabung

Stufe 1

Kognitive Komplexität

Stufe 1

Sprachlogische Komplexität

Stufe 0

Hilfestellungen:

Die Schülerinnen und Schüler könnten Schwierigkeiten haben, auf die Idee zu kommen, den Zusammenhang zwischen Masse und Volumen, also die Formel für die Dichte, zu nutzen.

Bei Auftreten dieses Problems können folgende Hilfestellungen gegeben werden:

Allgemein-strategische Hilfen	Inhaltsorientierte-strategische Hilfen	Inhaltliche Hilfen
Veranschauliche dir die Situation.	In welche Teilkörper lässt sich das Stehaufmännchen unterteilen? Denke daran, was du über diese bereits weißt.	Welche Formeln kennst du zur Berechnung des Volumens der Kugel und des Kegels?
Was ist gegeben und was wird gesucht?	Welche Größen kannst du in die Skizze eintragen? Helfen dir diese Größen die Aufgabe zu lösen?	Gibt es einen Zusammenhang zwischen der Höhe des Kegels und seinem Volumen? Wie kannst du diese Gleichung mit der gegebenen Information in Verbindung setzen, dass die Masse des Kegels höchstens genauso groß sein darf wie die der Halbkugel?
Kennst du Formeln, die dir weiterhelfen können?	Wie kannst du ausgehend davon, dass die Masse des Kegels höchstens genauso groß sein darf, wie die der Halbkugel, auf die maximale Höhe des Kegels schließen?	Welchen Zusammenhang zwischen Masse und Volumen kennst du? Denke an den Physik- oder Chemieunterricht!

Ein weiteres Problem könnte das Lösen der Gleichung sein.
Tritt dieses Problem auf, so kann auf folgende Weise darauf eingegangen werden:

Allgemein-strategische Hilfen	Inhaltsorientierte-strategische Hilfen	Inhaltliche Hilfen
Kennst du ähnliche Aufgaben?	Wie können wir Gleichungen umformen?	Wie ist das Volumen von Kegel und Halbkugel in Abhängigkeit von der Höhe?
Kannst du eine einfache lineare Gleichung lösen?	Welche Rechenoperationen kannst du hier verwenden?	Welche Größen beinhalten beide Terme?
Kannst du die Gleichung nach einer Variablen auflösen?	Betrachte den Kegel und die Halbkugel. Welche charakteristischen Größen haben sie gemeinsam?	Welche Größen sind jeweils relevant für das Volumen von Kegel und Halbkugel in Abhängigkeit von der Höhe?

Sozialformen:

Die Aufgabe soll in Einzelarbeit gelöst werden, damit die Lehrkraft einen Überblick über den Lernfortschritt jedes Schülers bekommt und in der folgenden Stunde auf die vorhanden Probleme eingehen kann.

Differenzierungsmöglichkeiten:

Differenzierungsmöglichkeiten für leistungsstärkere Schülerinnen und Schüler:

Die Aufgabe kann geringfügig geändert werden:

Ein Stehaufmännchen hat einen Durchmesser von 10 cm. Wie hoch darf der obere Teilkörper höchstens sein, wenn das Stehaufmännchen noch funktionieren soll?

Hier wird auf die Information "Damit das Stehaufmännchen funktioniert, müssen die beiden Körper gleich schwer sein." verzichtet. Dadurch erhöht sich der Schwierigkeitsgrad. Die Schülerinnen und Schüler müssen nun selbst eine Bedingung dafür finden, dass das Stehaufmännchen funktioniert.

Differenzierungsmöglichkeiten für leistungsschwächere Schülerinnen und Schüler:

Vereinfachung durch Visualisierung:

Ein Stehaufmännchen hat einen Durchmesser von 10 cm. Damit das Stehaufmännchen funktioniert, müssen die beiden Körper gleich schwer sein. Wie hoch darf der obere Teilkörper höchstens sein, wenn das Stehaufmännchen noch funktionieren soll?

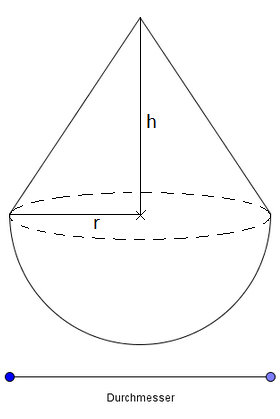
Die Schülerinnen und Schüler können nun besser erkennen, in welche Teilkörper sich das Stehaufmännchen unterteilen lässt und wonach gesucht ist. Möglicherweise kommen sie mithilfe der Skizze leichter darauf, das Volumen der Teilkörper zu berechnen.

Vereinfachung durch Lücken beheben:

Ein Stehaufmännchen hat einen Durchmesser von 10 cm. Damit das Stehaufmännchen funktioniert, müssen die beiden Körper gleich schwer sein. Wie hoch darf der obere Teilkörper höchstens sein, wenn das Stehaufmännchen noch funktionieren soll?

Hinweis: Nutze den Zusammenhang zwischen Masse und Volumen \(\varrho =\frac { m }{ V } \) (Formel für die Dichte \(\varrho \)).

Hier wird ein Hinweis gegeben, durch den die Schülerinnen und Schüler dahin gelenkt werden, die Volumenformel für den Kegel und die Halbkugel zu verwenden.

Die Stehaufmännchen-Aufgabe dient dem produktiven Üben der Kenntnisse über den Kegel und die Kugel, welche bereits im Unterricht eingeführt worden sind. Unter Verwendung der Volumenformeln dieser Körper wird der Frage nach der notwendigen Höhe eines Stehaufmännchens nachgegangen, wodurch diese Formeln gefestigt werden. Darüber hinaus wird das Lösen von Gleichungen wiederholt und geübt, sowie die Formel für die Dichte von Stoffen, welche aus dem Physikunterricht bereits bekannt sein sollte. Ein Fächerübergriff wird somit ermöglicht und den Schülerinnen und Schülern kann verdeutlicht werden, dass für das Lösen von Problemen auch Kenntnisse aus anderen Wissensgebieten von Bedeutung sein können.

Bearbeitet von: Robert Behrens (überarbeitet von Marisa Pfläging)

Like

Feedback