Streichholz-Quadrate

Fehlermeldung

Deprecated function: The each() function is deprecated. This message will be suppressed on further calls in FieldCollectionItemEntity->fetchHostDetails() (Zeile 313 von /www/htdocs/w0127817/beta.proffi-m.de/sites/all/modules/field_collection/field_collection.entity.inc).
Klasse Schulstufe Thema Themengebiet Schwierigkeit
3 Primarstufe Quadrate Raum und Form *
Heuristsche Hilfsmittel Heuristische Prinzipien Heuristische Strategien
Informative Figur Zerlegungs- und Ergänzungsprinzip, Invarianzprinzip, Symmetrieprinzip Systematisches Probieren

Aufgabenstellung

Wie viele Quadrate siehst du?

 

a) b) c)

 

 

Quellenangabe:

Original aus Rinkens, H., Rottmann, T., Träger, G. (Hrsg.). (2011). Welt der Zahl (3). Braunschweig: Schroedel. (S. 110)


Lösungsvariante 1 - Lösung durch Nachlegen der Figuren im Kopf
 

 

Die Aufgabenlösung wird sich jeweils im Kopf vorgestellt.

 

Aufgabenteil a)

gegeben: 

 

Lösung:

Zunächst werden drei Quadrate gelegt:

 

Im Anschluss daran werden im rechten unteren Quadrat zwei Streichhölzer hinzugefügt, sodass in diesem vier weitere kleine Quadrate entstehen.

Es ergeben sich damit drei große und vier kleine, also insgesamt sieben Quadrate.
 

 

 
Aufgabenteil b)

gegeben:

 

Lösung:

Zunächst wird ein großes Quadrat gelegt.

Wenn dieses mit vier Stäbchen geteilt wird, entstehen vier weitere Quadrate.

 
Wird nun in der Mitte noch ein Quadrat über das Kreuz gelegt, so entstehen vier weitere kleine Quadrate.

 

 
Durch Addition der Quadrate aus den einzelnen Schritten ergeben sich somit insgesamt zehn Quadrate.

 

Aufgabenteil c)
 
gegeben:

 

Lösung:

 
Hier erfolgt das Legen der Quadrate ähnlich wie in Aufgabenteil b)
 
Zunächst wird das gleiche große Quadrat gelegt wie in Aufgabenteil b). Hiermit existiert bereits ein Quadrat.

 
Dieses wird durch vier Stäbchen ebenfalls in vier weitere Quadrate geteilt.

 
Wird bei jedem dieser vier Quadrate die Ecke, die im Zentrum des großen Quadrats liegt, mit jeweils einem Stäbchen abgetrennt, so entsteht ein weiteres Quadrat.

 
Insgesamt ergeben sich in dieser Figur sechs Quadrate.

 

 

 
 
Lösungsvariante 2 - Lösung durch Abzählen

 

 

Die Quadrate werden jeweils im gegebenen Bild markiert und abgezählt.

 

Aufgabenteil a)

Durch Abzählen aller markierten Quadrate, erhält man sieben Quadrate.

 

 

Aufgabenteil b)

 

 Durch Einzeichnen der Quadrate, lassen sich insgesamt zehn Quadrate erkennen.

 

 

Aufgabenteil c)

 

 Hier lassen sich sechs Quadrate abzählen.

 

 


Die Problemlöseaufgabe lässt sich zu Beginn der dritten Klasse einsetzen. Da in der zweiten Klasse die ebene Figur 'Quadrat' bereits ausführlich behandelt wird (LISUM (2015), Niveaustufe B) und in der dritten Klasse komplexere ebene Figuren, wie beispielsweise das Parallelogramm und Trapez, sowie Körper folgen, wäre es sinnvoll, diese Aufgabe als Auffrischung des erlernten Wissens aus der zweiten Klasse zu nutzen. Sie kann aber natürlich auch schon in der zweiten Klasse im Rahmen der Unterrichtsthematik Quadrate als Übungsaufgabe eingesetzt werden.


Mit der Aufgabe Streichholz-Quadrate werden der inhaltsbezogene Kompetenzbereich [L3] Raum und Form sowie die prozessbezogenen Kompetenzbereiche [K2] Probleme mathematisch lösen, [K4] Mathematische Darstellungen verwenden und [K6] Mathematisch kommunizieren aus dem brandenburgischen Rahmenlehrplan (Teil C) Mathematik für die Jahrgangsstufen 1-10 (LISUM (2015)), der ab dem Schuljahr 2017/18 gültig ist, gefördert.

 

 

Inhaltsbezogene Kompetenzformulierungen

 

Raum und Form [L2]

Kompetenz 1: Die Schülerinnen und Schüler erkennen Quadrate in Figurenkonstellationen unter Benennung der Merkmale und Eigenschaften.

"Die Schülerinnen und Schüler können geometrische Objekte in der Umwelt wiedererkennen" (LISUM (2015), Geometrische Objekte und ihre Eigenschaften beschreiben, Niveaustufe A, S.26)

Erläuterung: Zum Lösen der Aufgabe benötigen die Kinder ihr Wissen über die Merkmale von Quadraten. Dieses Wissen müssen sie auf die Figurenkonstellationen anwenden.

 

Kompetenz 2: Die Schülerinnen und Schüler können eine Figurenkonstellation in ihre einzelnen Bestandteile (in Figuren) zerlegen.

"Die Schülerinnen und Schüler können ausgewählte geometrische Objekte unterscheiden" (LISUM (2015), Geometrische Objekte und ihre Eigenschaften beschreiben, Niveaustufe B, S.26), "Die Schülerinnen und Schüler können ausgewählte geometrische Objekte herstellen [...]" (LISUM (2015), Geometrische Objekte darstellen, Niveaustufe B, S.26)

Erläuterung: Die Kinder müssen die Abbilddung in alle möglichen einzelnen Quadrate zerlegen, um alle Quadrate zu erkennen.

 

Kompetenz 3:  Die Schülerinnen und Schüler erkennen Quadrate in unterschiedlichen Größen innerhalb der Figurenkonstellationen.

"Die Schülerinnen und Schüler können Lagebeziehungen zwischen geometrischen Objekten beschreiben" (LISUM (2015), Beziehungen zwischen geometrischen Objekten beschreiben, Niveaustufe B, S.26), "Die Schülerinnen und Schüler können ausgewählte geometrische Objekte unterscheiden" (LISUM (2015), Geometrische Objekte und ihre Eigenschaften beschreiben, Niveaustufe B, S.26)

Erläuterung: Um die richtige Anzahl bestimmen zu können, ist es notwendig zu wissen, dass Quadrate in unendlich vielen unterschiedlichen Größen auftreten können, ohne dass die Quadrateigenschaften verloren gehen.

 

 

Prozessbezogene Kompetenzformulierungen

 

Probleme mathematisch lösen [K2]

Kompetenz 4: Die Schülerinnen und Schüler finden einen Lösungsweg, um die Anzahl der Quadrate sicher zu bestimmen.

"Die Schülerinnen und Schüler können Lösungsstrategien [...] entwickeln und nutzen" (LISUM (2015), S.19)

Erläuterung: Die Kinder sollen dazu bewegt werden, ihre eigenen Lösungswege zu finden und anzuwenden. Dabei soll erkannt werden, dass es verschiedene Möglichkeiten der Lösungsfindung gibt.

 

Mathematische Darstellungen verwenden [K4]

Kompetenz 5: Die Schülerinnen und Schüler erstellen für die Lösung der Aufgabe geeignete graphische Abbildungen.

"Die Schülerinnen und Schüler können geeignete Darstellungen für das Bearbeiten mathematischer Sachverhalte und Probleme auswählen, nutzen und entwickeln" (LISUM (2015), S.20)

Erläuterung: Die Schülerinnen und Schüler müssen bei der Lösung die jeweilige Figurenkonstellation genauestens betrachten und es ist hilfreich diese zum Auszählen der Quadrate abzuändern. Es sollte erkannt werden, dass ein systematisches Vorgehen sinnvoll ist.  

 

Mathematisch kommunizieren [K6]

Kompetenz 6: Die Schülerinnen und Schüler dokumentieren ihren Lösungsweg in nachvollziehbarer Form.

"Die Schülerinnen und Schüler können eigene Problembearbeitungen und Einsichten dokumentieren und darstellen" (LISUM (2015), S.21)

Erläuterung: Die Lernenden müssen ihre Lösungsstrategie so festhalten, dass ein Außenstehender den Lösungsweg verstehen und nachvollziehen kann.   


Heuristische Hilfsmittel: 
  • Bei beiden Lösungswegen wird das Hilfsmittel der Infomativen Figur genutzt: Beim ersten Lösungsweg wird die Steichholzkonstellation mithilfe einer Informativen Figur schrittweise nachgebildet. Beim zweiten Lösungsweg werden in den gegebenen Abbildungen Quadrate markiert und letztendlich ausgezählt.

 

 

Heuristische Strategien: 
  • Beim ersten Lösungweg wird das Ergebnis gefunden, indem sich schrittweise von den großen zu den kleinen ebenen Figuren der Abbildung vorgearbeitet wird. Dabei sowie auch beim zweiten Lösungsweg wird jede einzelne Figur bezüglich des Vorhandenseins der Merkmale eines Quadrats betrachtet, was dabei hilft, jedes Quadrat zu finden, ohne eins zu übersehen. Somit spielt die Strategie des Systematischen Probierens bei der Aufgabenlösung eine Rolle.

 

  • Es existiert eine ähnliche Aufgabe in der Zeitschrift "MatheWelt" (Gebel, I. & Kuzle, A. (2016), S.8), in der Dreiecke in einer Figurenkonstellation abgezählt werden müssen. Wurde diese schon vorher im Unterricht eingesetzt, so ist bekannt, dass die gegebenen Abbildungen genauestens betrachtet werden müssen. Dieses Wissen über die Vorgehensweise bei der Aufgabe kann übertragen werden und somit werden in einem solchen Fall Analogieschlüsse gezogen.

 

 

Heuristische Prinzipien: 
  • Beim ersten Lösungsweg wird insbesondere das Ergänzungsprinzip angewendet, da die Figur schrittweise durch Legen der Streichhölzer im Kopf zur ursprünglichen Streichholzkonstellation ergänzt wird. Dies setzt auch ein vorheriges Zerlegen der urprünglichen Figur in große und kleine Quadrate im Kopf voraus. Auch beim zweiten Lösungsweg wird die ursprüngliche Figur in große und kleine Quadrate zerlegt. Somit ist das Zerlegungs- und Ergänzungsprinzip von Bedeutung.

 

  • Auch das Invarianzprinzip wird genutzt, da die Quadrate je nach Größe in unterschiedlicher Anzahl vorhanden sind und von den großen hin zu den kleinen Quadraten gearbeitet wird.

 

  • Außerdem gibt es Symmetrien zwischen den einzelnen Aufgabenteilen. So sind in allen Abbildungen die Quadrate mittlerer Größe enthalten, und in a) und b) die kleinsten Quadrate sowie in b) und c) jeweils das größte Quadrat. Durch Vergleich der Abbildungen kann somit bereits auf einen Teil der Anzahl der Quadrate geschlossen werden und somit ist es möglich, dass bei der Lösung auch das Symmetrieprinzip angewandt wird.

Die Aufgabe Streichholz-Quadrate hat nach Cohors-Fresenborg et al. mit insgesamt zwei erreichten Punkten einen Schwierigkeitsgrad von *.

 

 

Sprachlogische Komplexität: 

Die Aufgabenstellung besteht aus einem einfachen Hauptsatz, der allerdings keinen Aufschluss darüber gibt, welche Heurismen anzuwenden sind und in welcher Reihenfolge Schritte bei der Bearbeitung erfolgen müssen. Somit lässt sich der Aufgabe eine Sprachlogische Komplexität der Stufe 1 zuordnen.

 

 

Kognitive Komplexität: 

Bei beiden Lösungswegen sind Denkvorgänge nacheinander abzuarbeiten. So muss überlegt werden, wie am besten vorgegangen wird, damit keine Quadrate übersehen werden. Die Kognitive Komplexität der Aufgabe entspricht demnach ebenfalls der Stufe 1.

 

 

Formalisierung von Wissen: 

Die Formalisierung von Wissen lässt sich auf Stufe 0 ansiedeln, da die Lösung lediglich in graphischer Form (durch die erstellten Skizzen) und in rechnerischer Form (durch die Addition der Anzahlen der Quadrate unterschiedlicher Größen zu einer Gesamtzahl) erfolgt.

 

 

Formelhandhabung: 

Da lediglich zum Schluss die Anzahl der Quadrate addiert werden muss und dies nicht einmal in algebraischer Form ausgedrückt werden muss, lässt sich die Aufgabe bezüglich der Formelhandhabung ebenfalls auf Stufe 0 einordnen.

 

 

Stufenzuordnung: 
Formalisierung von Wissen
Stufe 0
Formelhandhabung
Stufe 0
Kognitive Komplexität
Stufe 1
Sprachlogische Komplexität
Stufe 1

Hilfestellungen: 

Bei der Bearbeitung der Aufgabe durch die Schülerinnen und Schüler können an einigen Stellen Schwierigkeiten auftreten. Im Folgenden sind zwei solcher kritischen Stellen dargestellt und es wird darauf eingegangen, welche allgemein-strategischen, welche inhaltsorientierten strategischen und welche inhaltlichen Hilfen in solchen Fällen gegeben werden können.

 

Ein erstes Problem könnte beim Finden einer geeigneten Lösungsstrategie auftreten. So könnten die Schülerinnen und Schüler nicht auf die Idee kommen, systematisch die Figuren im Kopf erneut zu legen, oder sich systematisch die verschiedenen Quadrate in der gegebenen Abbildung zu markieren. Dieses Problem kann darin zum Ausdruck kommen, dass die Schülerinnen und Schüler entweder gar nicht weiter kommen, oder dass sie bestimmte Quadrate am Ende übersehen haben. In solchen Fällen kann folgender Maßen interveniert werden:

 

Allgemein-strategische Hilfen Inhaltsorientierte strategische Hilfen Inhaltliche Hilfen
Helfen dir vielleicht weitere Skizzen? Kannst du im Kopf Streichhölzer entfernen, sodass noch Quadrate übrig bleiben? Du kannst dies auch mit weiteren Skizzen veranschaulichen! Welche unterschiedlichen Quadrate kannst du erkennen?
Kannst du das Gegebene irgendwie vereinfachen? Wie kannst du vorgehen, um alle Quadrate getrennt voneinander darzustellen? Überschneiden sich verschiedene Quadrate?

Falls die Aufgabe mit den Dreieckskonstellationen (vgl. Gebel, I. & Kuzle, A. (2016), S.8) bereits im Unterricht thematisiert wurde:

Kannst du dich an die Aufgabe mit den Dreiecken erinnern? Wie bist du dort vorgegangen?

 Du darfst auch mit verschiedenen Farben in die Abbildungen zeichnen! Welche Gemeinsamkeiten und Unterschiede haben die Quadrate die du sehen kannst? Was kannst du über ihre Lage sagen?

 

 

Ein grundlegenderes Problem kann darin liegen, dass die Schülerinnen und Schüler die Eigenschaften von Quadraten nicht mehr kennen und diese daher auch nicht in den Abbildungen identifizieren können, oder vielleicht sogar falsche Figuren als Quadrate identifizieren. Ist dies der Fall, so können folgende Hilfestellungen gegeben werden:

 

Allgemein-strategische Hilfen Inhaltsorientierte strategische Hilfen Inhaltliche Hilfen
Wie musst du vorgehen, wenn du Quadrate finden möchtest? Worauf musst du achten, wenn du Quadrate in der Abbildung finden möchstest? Welche Eigenschaften haben Quadrate?
Denke an die Eigenschaften von Quadraten und versuche diese in der Abbildung wiederzufinden. Was weißt du über die Streichhölzer? Was weißt du über die Seitenlängen eines Quadrats? Was kannst du über die Seiten von Quadraten sagen?
- Ein kleiner Hinweis: Alle Streichhölzer haben die gleiche Länge! Was sind Quadrate?

 

 

Sozialformen: 
  • Einzelarbeit

 

 

Differenzierungsmöglichkeiten: 

Für leistungsschwächere Schülerinnen und Schüler könnte die Aufgabe beispielsweise auf folgende Weise vereinfacht werden:

  • Durch Umlegen der Streichhölzer kann jeweils eine weiniger komplexere Figurenkonstellation zur Verfügung gestellt werden. Es könnten beispielsweise die folgenden vereinfachten Figuren durch die Aufgabenstellung zur Verfügung gestellt werden:
a) b) c)
In dieser Abbildung sind nur noch Quadrate gleicher Größe enthalten. Die Schülerinnen und Schüler müssen also nur noch abzählen. Es wird ihnen demnach ermöglicht, sich erst einmal an die Eigenschaften und Merkmale von Quadraten zurückzuerinnern, ohne verschiedene Größen und Überschneidungen berücksichtigen zu müssen.

Auch hier liegt eine Reduktion der verschiedenen Größen der Quadrate vor. So müssen die Lernenden nicht mehr drei verschiedene Größen unterscheiden, sondern nur noch zwei. Außerdem ist es möglich, dass sich die Lernenden die Überschneidung der großen Quadrate besser vorstellen können als in dem ursprünglichen Bild, da diese in einem ganzen kleineren Quadrat übereinstimmen, sich aber nicht vollständig überdecken (vgl. Bild unten). Dadurch könnte ihnen die Anwendung bestimmter Heurismen (auch für Aufgabenteil c)) nahegelgt werden.

Bei dieser Abbildung wurde das Quadrat aus dem Zentrum entnommen und dafür wurde eines der vier Quadrate im großen Quadrat mit zwei Streichhölzern geviertelt. Somit sind keine Dreiecke mehr vorhanden, die die Schülerinnen und Schüler von Quadraten differenzieren müssen und es ist auch kein Quadrat mehr vorhanden, dass im Lageverhältnis zu den anderen Quadraten um verdreht ist.

 

 

  • Den Schülerinnen und Schülern könnte eine Abbildung (Musterlösung) als Hilfe vorgegeben werden, in der eine Figurenkonstellation Schritt für Schritt erstellt wird und somit eine Erleichterung vorliegt (beispielsweise für Aufgabenteil a), wie in Lösungsvariante 1).

 

 

Auch für leistungsstärkere Schülerinnen und Schüler kann die Aufgabe schwieriger gestaltet werden, indem zum Beispiel folgende Änderungen vorgenommen werden:

  • Es können komplexere Figurenkonstellationen mit mehr Stäbchen erstellt werden. Eine veränderte Aufgabenstellung könnte wie folgt aussehen:
a) b) c)
Hier müssen die Schülerinnen und Schüler mehr Quadrate abzählen als in der ursprünglichen Aufgabe, wodurch sich der Arbeitsaufwand erhöht. Auch hier müssen mehr Quadrate abgezählt werden. Im Vergleich zur ursprünglichen Aufgabe wird das zentrale Quadrat durch zwei zusätzliche Stäbchen geviertelt. Die Schwierigkeit liegt nun darin, dass mehr Quadrate abzuzählen sind, vier verschiedene Größen der Quadrate auftreten, fünf der Quadrate um 45° rotiert sind und die kleinen Quadrate aufgrund der Diagonalen im zentralen Quadrat nicht auf den ersten Blick zu erkennen sind.

 

  • Es könnte eine weitere Frage gestellt werden: Kannst du noch weitere Figuren außer Quadrate in den Strochholz-Bildern erkennen?

Im Bild zum Aufgabenteil b) können neben Quadraten auch Dreiecke identifiziert werden. Durch die Identifikation dieser Figuren müssen die Schülerinnen und Schüler zusätzlich zwischen Quadraten und Dreiecken und deren unterschiedlichen Eigenschaften differenzieren.

 

  • Daneben kann den Schülerinnen und Schülern eine weitere ebene Figur gegeben werden, in der auch andere Figuren enthalten sind. Es könnte die Aufgabe gegeben werden, auch in diesen Figuren Quadrate zu finden und im Anschluss daran die Zusatzaufgabe, weitere - vielleicht auch unbekannte - Figuren zu finden. Damit könnte auch ein fließenderer Übergang zur neuen Unterrichtsthematik geschaffen werden, indem auch noch unbekannte ebene Figuren auftreten, die am Ende visualisiert werden und die dann im folgenden Unterricht aufgegriffen und vertieft thematisiert werden. Beispiele für solche Zusatzfiguren könnten die folgenden sein:

Hier lassen sich fünf Quadrate erkennen.

Darüber hinaus sind auch Dreiecke und Trapeze zu finden.

Diese Figurenkonstellation besteht aus einem Quadrat.

Es lassen sich auch Dreiecke, Parallelogramme und Trapeze identifizieren.

 Die Schwierigkeit bei dieser Konstellation besteht darin, dass zwar Dreiecke, Parallelogramme, ein Rechteck und ein Trapez zu finden sind, jedoch kein Quadrat, obwohl danach in der Aufgabenstellung gefragt wird.

 

  • Zur Forderung von Schülerinnen und Schülern, die früher mit der Aufgabe fertig sind, könnte außerdem folgende Zusatzaufgabe gegeben werden:

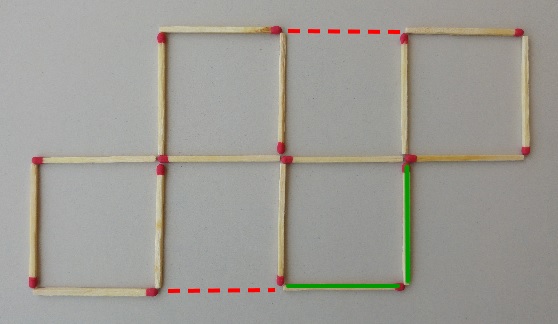
Lege zwei Streichhölzer so um, dass anschließend nur vier Quadrate zu sehen sind!

 

Lösung:

Also ergibt sich folgende Streichholzkonstellation:

 

 


Diese Aufgabe lässt sich zu Beginn der dritten Klasse als Einstieg in den Themenkomplex zu weiteren ebenen Figuren und Körpern einsetzen. So können Merkmale und Eigenschaften von bereits aus der zweiten Klasse bekannten Figuren - den Quadraten - noch einmal wiederholt und gefestigt werden.

Somit lässt sich die Aufgabe auch als Übungsaufgabe nach der Behandlung von Quadraten und deren Eigenschaften einsetzen. Um den Themenbereich der Quadrate vollständig zu vertiefen, reicht diese Aufgabe jedoch nicht aus. Sie ist lediglich eine gute Möglichkeit, die Kinder dazu anzuregen, ihr angeeignetes Wissen kreativ anzuwenden.



Bearbeitet von: Anna-Victoria Müller, Julia Hitscher (ergänzt von Marisa Pfläging)
nach oben
415 Nutzer/-innen haben abgestimmt.

Feedback

Wir freuen uns auf Ihre Anregungen und konstruktive Rückmeldung zum Material.