Trigonometrische Berechnungen am Dreieck

Fehlermeldung

Deprecated function: The each() function is deprecated. This message will be suppressed on further calls in FieldCollectionItemEntity->fetchHostDetails() (Zeile 313 von /www/htdocs/w0127817/beta.proffi-m.de/sites/all/modules/field_collection/field_collection.entity.inc).
Klasse Schulstufe Thema Themengebiet Schwierigkeit
7/ 8/ 9/ 10 Sekundarstufe I Trigonometrische Sätze Größen und Messen, Raum und Form **

Aufgabenstellung

Berechne die fehlenden Seiten und Winkel in einem Dreieck ABC mit a = 17,1 cm, wᵧ = 10,2 cm und γ = 63,8°.

Quellenangabe:

Original aus Lambacher Schweizer 10, Nordrhein- Westfalen (S.195, Nr.10)


Lösungsvariante 1 - Rechnerische Lösung
 
Zunächst wird eine Skizze mit den gegebenen Größen angefertigt.
 
 
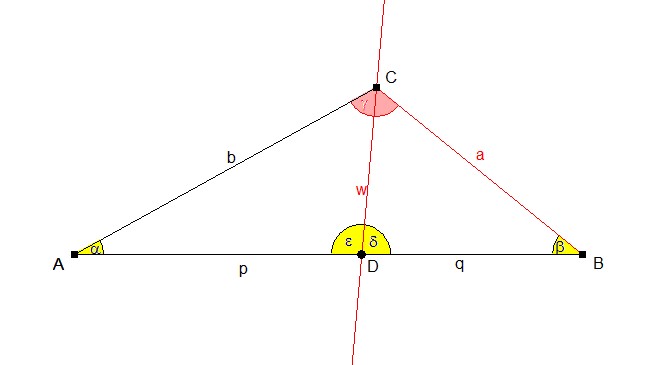
Durch die Winkelhalbierende wᵧ ergeben sich zwei Dreiecke. Den Schnitt der Winkelhalbierenden mit der Seite c nennen wir D. wᵧ  teilt c in p und q und den Winkel γ in zwei gleich große Winkel, die jeweils 31,9° betragen.  Den Winkel \(\sphericalangle BDC\) nennen wir δ, den Winkel \(\sphericalangle ADC\) ε.
 

Zu berechnen sind die Winkel α und β und die Seiten b und c.
 
 
1. Berechnung der Seite q im Dreieck BCD mit dem Kosinussatz: 
 
\(q² = a²+ w_\gamma² - 2\cdot a\cdot w_\gamma\cdot cos(\frac { \gamma }{ 2 } )\)
\(q^2=(17,1cm)^2+(10,2cm)^2-2\cdot 17,1cm \cdot 10,2cm\cdot cos⁡(31,9°)\)
\(q^2≈100,29 cm \)
\( q≈10,01 cm\)
 
\(\Leftrightarrow \)
 
\(\Rightarrow \)
\(\Rightarrow \)
 
 
 
2. Berechnung des Winkels β im Dreieck BCD mit dem Kosinussatz: 
 
\(w_\gamma² = a²+ q² - 2\cdot a\cdot q\cdot cos(\beta )\)
\(cos(\beta )=\frac { a²+q²-{ w }_{ \gamma }² }{ 2\cdot a\cdot q } \)
\(cos(\beta )=\frac { (17,1cm)²+(10,01cm)²-(10,2cm)² }{ 2\cdot 17,1cm\cdot 10,01cm } \)
\( β≈32,55°\)
 
 
\(\Leftrightarrow \)
\(\Rightarrow \)
\(\Rightarrow \)
 
 
3. Berechnung des Winkels α mit dem Innenwinkelsummensatz:
 
\(α=180°- β- γ\)
\(α≈180°-32,55°-63,8°\)
\(α ≈83,65°\)
 
 
\(\Rightarrow \)
\(\Rightarrow \)
 
 
4. Berechnung des Winkels δ mit dem Innenwinkelsummensatz: 
 
\(δ=180°- β- \frac { \gamma }{ 2 } \)
\(δ ≈180°-32,55°-31,9°\)
\(δ ≈115,55°\)
 
 
\(\Rightarrow \)
\(\Rightarrow \)
 
 
5. Berechnung des Winkels ε mit dem Nebenwinkelsatz: 
 
\(ε=180°- δ\)
\(ε ≈180°-115,55°\)
\(ε ≈64,45°\)

 

 
\(\Rightarrow \)
\(\Rightarrow \)
 
 
6. Berechnung der Seite p  im Dreieck ADC mit dem Sinussatz:
 
\(\frac { p }{ sin(\frac { \gamma }{ 2 } ) } =\frac { { w }_{ \gamma } }{ sin(\alpha ) } \)
\(p=\frac { { w }_{ \gamma } }{ sin(\alpha ) } \cdot sin(\frac { \gamma }{ 2 } )\)
\(p=\frac { 10,2cm }{ sin(83,65°) } \cdot sin(31,9°)\)
\(p ≈5,42cm\)
 
 
\(\Leftrightarrow \)
\(\Rightarrow \)
\(\Rightarrow \)
 
 
 
7. Berechnung der Seite c durch Addition von p und q:
 
\(c=p+q\)
\(c≈ 5,42cm+10,01cm\)
\(c≈15,43 cm\)
 
 
\(\Rightarrow \)
\(\Rightarrow \)
 
 
8. Berechnung der Seite b im Dreieck ABC mit dem Sinussatz: 
 
\(\frac { b }{ sin(\beta ) } =\frac { a }{ sin(\alpha ) } \)
\(b=\frac { a }{ sin(\alpha ) } \cdot sin(\beta )\)
\(b=\frac { 17,1cm }{ sin(83,65°) } \cdot sin(32,55°)\)
\(b≈9,26cm\)
 
 
\(\Leftrightarrow \)
\(\Rightarrow \)
\(\Rightarrow \)
 
 
 
Die Seite b des Dreiecks ABC hat demnach eine Länge von 9,26cm, die Seite c eine Länge von 15,43cm, der Winkel \(\alpha \) beträgt 83,65° und der Winkel \(\beta \) beträgt 32,55°.
 

 
Lösungsvariante 2 - Zeichnerische Lösung
 
Bei der zeichnerischen Bearbeitung der Aufgabe wird eine Skizze mit den gegebenen Größen nachkonstruiert und im Anschluss daran werden alle fehlenden Winkel und Seiten gemessen.

Die Konstruktion erfolgt mit Zirkel und Geodreieck mithilfe der dynamischen Geometriesoftware EUKLID DynaGeo:

 
1. Konstruktion der Seite a = 17,1 cm und des Winkels γ = 63,8°.
 
 
 
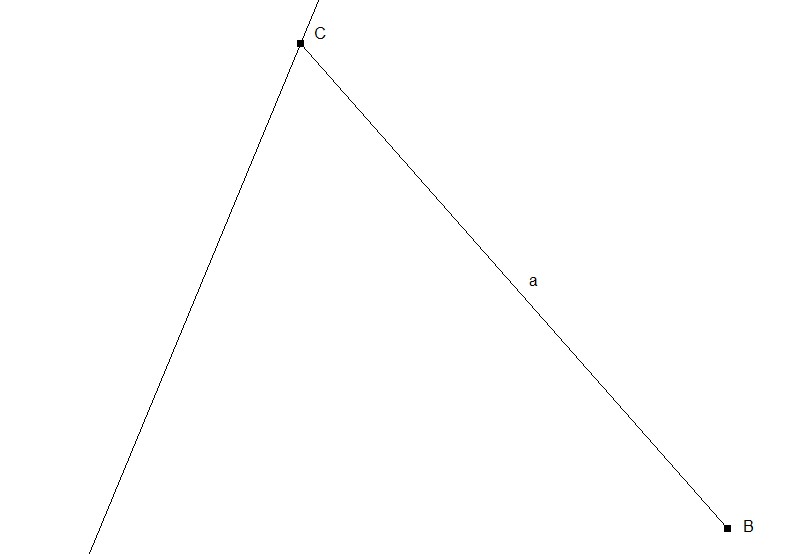
2. Konstruktion der Winkelhalbierenden wᵧ = 10,2 cm am Punkt C mit Hilfe einer Winkelhalbierenden und eines Kreises mit Radius r = 10,2 cm um C.
Der Schnittpunkt gibt uns den Punkt D.
 
 
 
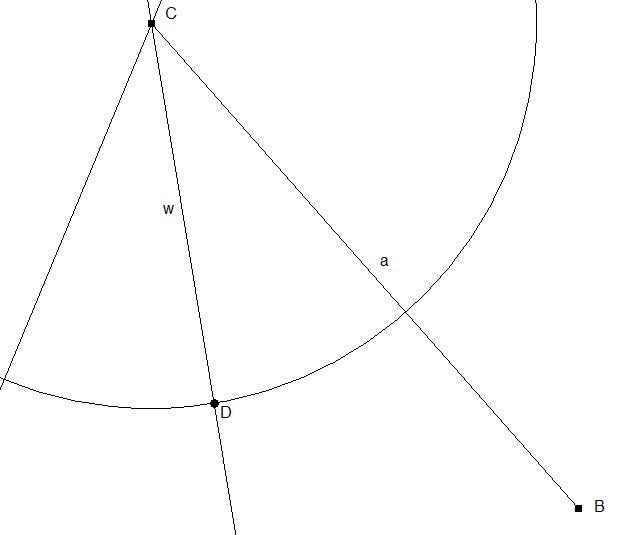
3. Konstruktion der Seite c mit p und q durch B und D. Der Schnittpunkt mit der Halbgeraden liefert uns den Punkt A und somit die Seite b.
 
 
 
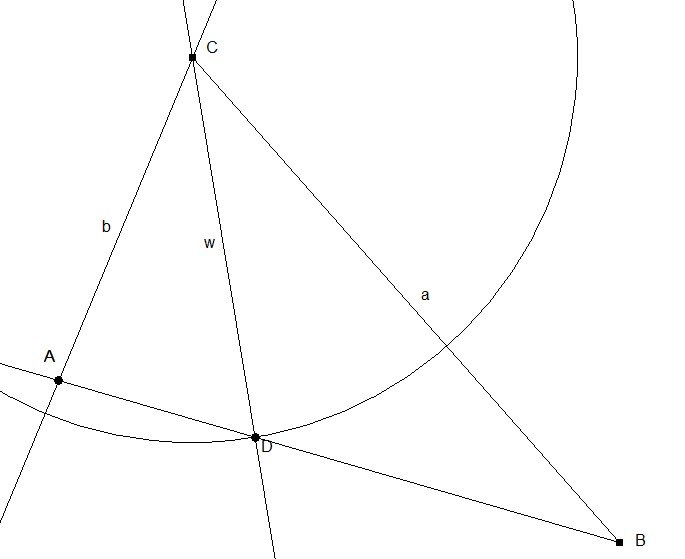
4. Messen der fehlenden Seiten b und c und der fehlenden Winkel α und β.
 
 
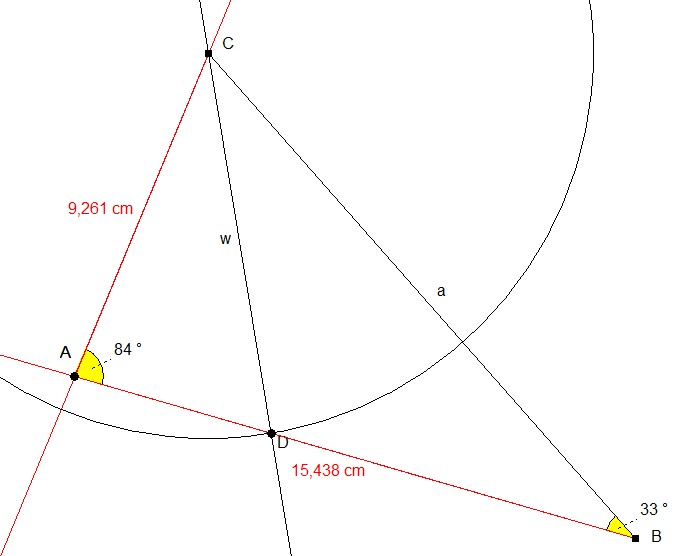
Es ergeben sich für die gesuchten Größen des Dreiecks ABC \(b\approx 9,261cm\), \(c\approx 15,438cm\), \(\alpha \approx 84°\) und \(\beta \approx 33°\).
 

Die Aufgabe lässt sich in der 10. Jahrgangsstufe einsetzen, da sie gewisse Grundlagen im trigonometrischen Bereich benötigt. So müssen die SuS den Umgang mit dem Kosinus- und Sinussatz bereits in der Schule gelernt haben. Dies geschieht laut niedersächsischem Kerncurriculum des Faches Mathematik für das Gymnasium für die Schuljahrgänge 5 bis10 (im Folgenden als "KC Niedersachsen Gymnasium (Jh.5-10)" bezeichnet) erst in der 10. Klasse: „Die Schülerinnen und Schüler berechnen Streckenlängen und Winkelgrößen mit Hilfe von Ähnlichkeitsbeziehungen und trigonometrischen Beziehungen“ (KC Niedersachsen Gymnasium (Jh.5-10), S.29). Zusätzlich benötigen die SuS das Wissen über Termumformung, welches ebenfalls erst in der 10. Klasse erlernt werden soll: „Die Schülerinnen und Schüler nutzen Tabellen, Grafen, Terme und Gleichungen zur Bearbeitung funktionaler Zusammenhänge." (ebd., S.21), "[Sie] formen Terme um, ggf. auch mit einem Computer-Algebra-System." (ebd.), "[Sie] wählen geeignete Verfahren zum Lösen von Gleichungen“ (ebd.). All dies wird von den SuS in der Aufgabe verlangt.

Der alternative Lösungsweg, das genaue Konstruieren des Dreiecks, ist bereits mit dem Wissenstand einer 7./8. Klasse einsetzbar, da die SuS in diesen Jahrgangsstufen die Winkelhalbierende kennen lernen. Ohne das Wissen über diese Hilfslinie im Dreieck ist das Dreieck nicht konstruierbar. „Die Schülerinnen und Schüler kennen Höhen, Mittelsenkrechte, Seitenhalbierende und Winkelhalbierende als besonderen Linien im Dreieck." (ebd. S.32), "[Sie] beschreiben und erzeugen Kreis, Parallele, Mittelsenkrechte, Winkelhalbierende und Parabel als Ortslinien“ (ebd.).

Inhaltsbezogene Kompetenzformulierungen
 
 
Größen und Messen
  • Die SuS verfügen über Größenvorstellungen, welche im Modellierungsprozess helfen, die Ergebnisse auf Plausibilität zu überprüfen.
 
  • Die SuS haben ein grundlegendes Verständnis vom Prinzip des Messens und können mit Größen umgehen.  
Größen und Messen, "Die Schülerinnen und Schüler entwickeln ein grundlegendes Verständnis vom Prinzip des Messens." (KC Niedersachsen Gymnasium (Jh. 5-10) 2006, S.29); zusätzlich am Ende von Schuljahrgang 10 "Die Schülerinnen und Schüler berechnen Streckenlängen und Winkelgrößen mit Hilfe von [...] Trigonometrischen Beziehungen." (ebd.)
 
 
Raum und Form
Bei der von uns ausgewählten Aufgabe ist es sehr hilfreich, vor dem Berechnen der fehlenden Größen eine Skizze anzufertigen. An dieser kann man die Struktur des Lösungsweges erkennen und sich vorstellen, welche Eigenschaften oder Funktionen die fehlenden Seitenlängen und Winkelgrößen innerhalb des Dreiecks besitzen können. Außerdem erfolgt ein ständiger Wechsel zwischen dem Herstellen, dem Darstellen, dem Beschreiben, dem Berechnen der Skizze und der Formelanwendung. Sobald die SuS eine unbekannte Seite oder einen unbekannten Winkel berechnet haben, ist es hilfreich die Skizze noch einmal zu betrachten und mithilfe neuer Erkenntnisse der Lösung näher zu kommen. Somit wird durch die Aufgabe die folgende Kompetenz gefördert:
  • Die SuS können eine Zeichnung (Skizze) konstruieren, mit Konstruktionsbezeichnungen umgehen sowie Muster und Strukturen erkennen.
Raum und Form, zusätzlich am Ende von Schuljahrgang 8 "Die Schülerinnen und Schüler konstruieren mit Zirkel, Geodreieck und dynamischer Geometriesoftware [...]." (KC, Niedersachsen Gymnasium (Jh. 5-10) 2006, S.31)
 
 
Zahlen und Operationen
  • Die SuS verfügen über ein Verständnis der Zahlen, Variablen, Rechenoperationen, Terme und Formeln.
Zahlen und Operationen "Die Schülerinnen und Schüler entwickeln ein grundlegendes Verständnis von Zahlen, Variablen, Rechenoperationen, Umkehrungen, Termen und Formeln." (KC, Niedersachsen Gymnasium (Jh. 5-10) 2006, S.25)
  • Die SuS operieren unter Verwendung des Kosinussatzes, Sinussatzes, des Nebenwinkel-Satzes und des Innenwinkelsummensatzes mit Variablen im jeweiligen Zahlenbereich.
 Zahlen und Operationen, zusätzlich am Ende von Schuljahrgang 8 "Die Schülerinnen und Schüler lösen einfache Rechenaufgaben im Bereich der reellen Zahlen" (KC, Niedersachsen Gymnasium (Jh. 5-10) 2006, S.25)
 
 
 
Prozessbezogene Kompetenzformulierungen
 
 
Mathematische Darstellungen verwenden
Die SuS fertigen zunächst eine Skizze mit dem gegebenen Winkel und den gegebenen Seiten an,daraufhin zeichnen sie auch die fehlenden Seiten und Winkel ein. Die Skizze veranschaulicht die logischen und geometrischen Zusammenhänge der gegebenen und der gesuchten Größen des Dreiecks. Außerdem können die SuS ihre individuellen Überlegungen anhand der Skizze dokumentieren. An dieser Skizze können sich die SuS im weiteren Verlauf ihres Lösungsweges orientieren. Außerdem unterstützt sie die Argumentation des Lösungsweges der SuS.
Mathematische Darstellungen verwenden "Mathematisches Arbeiten erfordert das Anlegen und Interpretieren von Darstellungen und den problemangemessenen Wechsel zwischen verschiedenen Darstellungen.", "Eigene Darstellungen dienen dem Strukturieren und Dokumentieren individueller Überlegungen und unterstützen die Argumentation." (KC, Niedersachsen Gymnasium (Jh. 5-10) 2006, S.19)
 
 
Mit symbolischen, formalen und technischen Elementen der Mathematik umgehen
  • Die SuS wählen verschiedene Sätze (Kosinussatz, Sinussatz, Nebenwinkel-Satz und Innenwinkelsummen-Satz), also Verfahren und Werkzeuge zur Berechnung der fehlenden Winkel und Seiten aus, wenden diese an und bewerten sie.
Mit symbolischen, formalen und technischen Elementen der Mathematik umgehen, zusätzlich am Ende von Schuljahrgang 6 "Die Schülerinnen und Schüler stellen einfache mathematische Situationen durch Terme dar und interpretieren Variable und Terme in gegebenen Situationen." (KC, Niedersachsen Gymnasium (Jh. 5-10) 2006, S.21)
  • Die SuS benutzen zur Berechnung der Winkel mithilfe von trigonometrischen Funktionen den Taschenrechner.
Mit symbolischen, formalen und technischen Elementen der Mathematik umgehen, zusätzlich am Ende von Schuljahrgang 8 "Die Schülerinnen und Schüler nutzen den eingeführten Taschenrechner und Geometriesoftware zur Darstellung und Erkundung mathematischer Zusammenhänge sowie zur Bestimmung von Ergebnissen." (KC, Niedersachsen Gymnasium (Jh. 5-10) 2006, S.22)
 
 
Probleme mathematisch lösen
Die Lösungsstruktur ist nicht offensichtlich, da zunächst verschiedene Winkelgrößen und Seitenlängen von Teildreiecken berechnet werden müssen, um anschließend die fehlenden Größen der Winkel und Seiten des gegebenen Dreiecks zu berechnen. Die Lösung der Aufgabe erfordert also ein strategisches Vorgehen. Um die Aufgabe zu lösen müssen die SuS über solides Grundwissen verfügen, sie müssen die oben genannten Sätze kennen und diese flexibel anwenden. Die SuS erfahren durch die Aufgabe und durch das schrittweise Lösen des Problems, dass Anstrengungsbereitschaft und Durchhaltevermögen zu Erfolg führen.
Probleme mathematisch lösen, zusätzlich am Ende von Schuljahrgang 8  „Die Schülerinnen und Schüler stellen sich inner- und außermathematischen Problemen und beschaffen die zu einer Lösung noch fehlenden Informationen."(KC, Niedersachsen Gymnasium (Jh. 5-10) 2006, S.15); zusätzlich am Ende von Schuljahrgang 10 "[Sie] wählen geeignete heuristische Strategien zum Problemlösen aus und wenden diese an.“ (ebd., S.16)

Heuristische Hilfsmittel: 
  • Die SuS erstellen zunächst eine Skizze, diese ist eine informative Figur. An ihr kann man alle wichtigen Informationen, die in der Aufgabe enthalten sind, ablesen und so wesentlich leichter eine Lösungsidee finden.
 
  • Des Weiteren werden Gleichungen als heuristisches Hilfsmittel verwendet, im konkreten Fall der Kosinussatz und der Sinussatz. Mithilfe von diesen Gleichungen können Beziehungen zwischen den gegebenen Größen unter Verwendung von Variablen hergestellt werden und diese zielführend mit mathematischen Mitteln umgeformt und schrittweise gelöst werden.
 
 
Heuristische Strategien: 
  • Als heuristische Strategie ist das kombinierte Vorwärts- und Rückwärtsarbeiten von Bedeutung. Um die Lösung zu erhalten, sind bei dieser Aufgabe mehrere Schritte erforderlich, man versucht aus dem Gegebenen das Gesuchte zu ermitteln - es wird vorwärtsgearbeiten. Des Weiteren werden Teilergebnisse mithilfe geeigneter Dreiecke ermittelt, um alle Größen des Ausgangsdreiecks zu erhalten. Es gibt bei dem Lösungsweg also immer neue Teilziele mit sich wiederholenden Rechenschritten: Es wird immer wieder eine Seite oder ein Winkel mithilfe der trigonometrischen Sätze und Winkelsätze neu berechnet, um letztendlich die gesuchten Winkelgrößen und Seitenlängen zu erhalten. Dies ist die Strategie des Rückwärtsarbeiten. Beide Strategien werden hier kombiniert, um die Lösung zu erhalten.
 
  • Eine weitere Strategie, die den SuS helfen kann, ist die des Analogieschlusses. Da die SuS bereits den Kosinus- und Sinussatz kennen gelernt und an einfachen Beispielaufgaben angewendet haben sollten, könnten die SuS ihr Wissen aus bekannten Aufgaben nutzen, um die Lösung der Teilschritte zu erhalten.
 
 
Heuristische Prinzipien: 
  • Bei der Lösung der Aufgabe hilft das heuristische Prinzip des Zerlegens und Ergänzens. Das Dreieck wird in Teildreiecke unterteilt, um Bekanntes, wie zum Beispiel die Länge der Winkelhalbierenden, zu verwenden und um mit Teilberechnungen die gesuchte Lösung zu ermitteln.

Für die Aufgabe ergibt sich nach Cohors-Fresenborg et al mit ingesamt 5 erreichten Punkten ein Schwierigkeitsgrad von **.
 
 
Sprachlogische Komplexität: 
Die SuS müssen die relevanten Informationen der Aufgabe verstehen, wie zum Beispiel den Fachbegriff Winkelhalbierende. Des Weiteren ist in dem Aufgabentext keine Reihenfolge festgelegt, die die Lösungsstruktur aufzeigen könnte. Daher lässt sich die Aufgabe bzgl. der Sprachlogischen Komplexität nach Cohors-Fresenborg et al. der Schwierigkeitsstufe 1 zuordnen.
 
 
Kognitive Komplexität: 
Die Kognitive Komplexität ist hier besonders ausgeprägt. Die SuS müssen mehrere Denkprozesse parallel durchführen. Es gibt mehrere Dreiecke, die zu betrachten sind und es muss immer wieder gefragt werden, welche Informationen gegeben sind und was zielführend ist. Außerdem sind die Denkschritte in einer zu beachtenden Reihenfolge verkettet, die SuS müssen beachten, welche Winkelgröße oder Seitenlänge sie zuerst berechnen können und ob es überhaupt sinnvoll ist, diese zu berechnen. Die Schwierigkeitsstufe des Aufgabenmerkmals liegt somit bei 2.
 
 
Formalisierung von Wissen: 
Die Formalisierung des Wissens ist nicht so komplex wie die Kognitive Komplexität und ist bei Schwierigkeitsstufe 1 angesiedelt. Die SuS müssen geeignete Werkzeuge (den Kosinussatz, den Sinussatz, den Nebenwinkelsatz und den Innenwinkelsummensatz) nutzen. Da sie die Sätze schon vorher im Unterricht behandelt haben, sollten ihnen diese Werkzeuge bekannt sein.
 
 
Formelhandhabung: 
Auch das Aufgabenmerkmal Formelhandhabung ist der Schwierigkeitsstufe 1 zu zuordnen. Die oben genannten Sätze müssen nicht nur von den SuS angewendet werden, sie müssen auch umgeformt werden.
 
 
Stufenzuordnung: 
Formalisierung von Wissen
Stufe 1
Formelhandhabung
Stufe 1
Kognitive Komplexität
Stufe 2
Sprachlogische Komplexität
Stufe 1

Hilfestellungen: 
 
Bei der Bearbeitung der Aufgabe befindet sich bereits in der ersten Phase des Problemlösens "Verstehen der Aufgabe" (nach Pólya 1948) eine kritische Stelle. Die SuS sollten ohne Probleme herausarbeiten können was gesucht und was gegeben ist, jedoch könnte es Schwierigkeiten bei der Erstellung einer informativen Figur/Skizze als Hilfe geben. Andere SuS könnten gar nicht erst auf die Idee kommen, eine Skizze zu erstellen, um die gesuchten und gegebenen Informationen der Aufgabe zu veranschaulichen. In diesem Fall können folgende Hinweise gegeben werden.
 
Allgemein-strategische Hilfen
Wie beginnen wir bei Problemlöseaufgaben für gewöhnlich?
Unterstreiche dir das wichtigste im Text.
Fertige doch eine Skizze an.
 
 
Die wahrscheinlich größte Hürde bei der Lösung der Aufgabe liegt in Phase 2, "Ausdenken eines Planes" (Pólya 1948). Die SuS müssen sich überlegen, wie sie vorgehen, um die gesuchten Größen zu ermitteln. Aber wo fängt man an? Um die SuS dabei zu unterstützen können folgende Hilfen gegeben werden.
 
Allgemein-strategische Hilfen Inhaltsorientierte strategische Hilfen Inhaltliche Hilfen
Kennst du ähnliche Aufgaben, und was hat dir dort geholfen?
Kannst du bekannte Sätze über Winkel anwenden?
Welche Winkel der Skizze kannst du direkt berechnen?
Markiere dir die gegebenen Seiten und Winkel in deiner Skizze.
Wie helfen dir die Teildreiecke?
Was macht die Winkelhalbierende mit dem Winkel \(\gamma \)?
 
Welche Sätze über Dreiecke könnten dir hier weiterhelfen?
Wie lauten Kosinus- und Sinussatz?
 
 
Eine weitere kritische Stelle ist das Umstellen von Kosinus- und Sinussatz. Hier können folgende Hinweise helfen.
 
Allgemein-strategische Hilfen Inhaltsorientierte strategische Hilfen Inhaltliche Hilfen
Wie stellt man Gleichungen um?
Nach was möchtest du die Gleichung umstellen?
Stelle den Kosinussatz nach β um, bzw. stelle den Sinussatz nach p bzw. b um.
Kennst du eine ähnliche Aufgabe?
Was möchtest du berechnen?
Addiere/Multipliziere/Subtrahiere/Dividiere … mit ... .
Überprüfe deinen Lösungsweg.
Überprüfe deine Ergebnisse an deiner Skizze und dem Aufgabentext.
Kontrolliere dein Ergebnis mit dem Innenwinkel- und dem Nebenwinkelsatz.
 
Macht deine Lösung Sinn?
  
 
 
 
Sozialformen: 
  • Einzelarbeit
  • Partnerarbeit
 
 
Differenzierungsmöglichkeiten: 
Differenzierungen in der Aufgabe selbst gibt es keine.
 
Für leistungsschwächere SuS kann die Aufgabe folgender Maßen differenziert werden:
Den SuS, die sich bei der Aufgabe nicht allein die Lösungsidee erschließen können, kann eine bereits erstellte Skizze auf dem Pult oder der Rückseite der Tafel zur Verfügung gestellt wird. Falls dies nicht weiterhilft, könnte die Lehrperson ein weiteres Blatt Papier mit den notwendigen Sätzen auf das Pult legen, an das sich die SuS orientieren können. Diese Hilfen sollten jedoch erst nach einer gewissen Selbstbeschäftigung mit der Aufgabe stattfinden, damit jeder die Möglichkeit hat sich eine eigene Lösungsidee zu erschließen und diese auszuprobieren, bevor er/sie zu schnell aufgibt.
 
Leistungsstärkeren SuS kann zusätzlich die Aufgabe gestellt werden, einen anderen Lösungsweg zu finden oder eine Möglichkeit zu finden die errechnete Lösung durch Nachkonstruieren zu überprüfen.
 

Die Aufgabe ist eher zum Ende der Thematik „Trigonometrie“ in der 10. Jahrgangsstufe einsetzbar. Es werden wichtige Sätze der Unterrichtseinheit in einer komplexeren Aufgabe wiederholt. Sie schult den Umgang mit dem Kosinus- und dem Sinussatz und zeigt den SuS noch einmal, dass diese Sätze zur Berechnung von Winkelgrößen und Seitenlängen in nicht rechtwinkligen Dreiecken einsetzbar sind. Durch das Umformen der Terme werden auch die verschiedenen Einsatzmöglichkeiten des Kosinussatzes und des Sinussatzes deutlich. Da es sich nicht um eine Päckchenaufgabe handelt lernen die SuS wie Sätze oder Formeln mehrmals (hintereinander) angewendet werden können. Außerdem fördert diese Übung das schrittweise Problemlösen. Die Aufgabe ist jedoch noch vor dem Bearbeiten alltagsbezogener Aufgaben einzusetzen, da das Problem der Aufgabe rein mathematisch ist und keine Modellierung stattfindet, sondern lediglich eine Darstellung des Problems anhand der Skizze.
 


Bearbeitet von: Lisa Sölter, Lea Stöcker, Maike Schleper (hochgeladen von Marisa Pfläging)
nach oben
407 Nutzer/-innen haben abgestimmt.

Feedback

Wir freuen uns auf Ihre Anregungen und konstruktive Rückmeldung zum Material.