Falten eines Fünfecks
| Klasse | Schulstufe | Thema | Themengebiet | Schwierigkeit |
|---|---|---|---|---|
| 8/ 9/ 10 | Sekundarstufe I | Begründen in der ebenen Geometrie | Größen und Messen, Raum und Form | ** |
| Heuristsche Hilfsmittel | Heuristische Prinzipien | Heuristische Strategien |
|---|---|---|
| Informative Figur | Zerlegungs- und Ergänzungsprinzip | Vorwärtsarbeiten, Rückwärtsarbeiten, Kombiniertes Vorwärts- und Rückwärtsarbeiten |
Aufgabenstellung
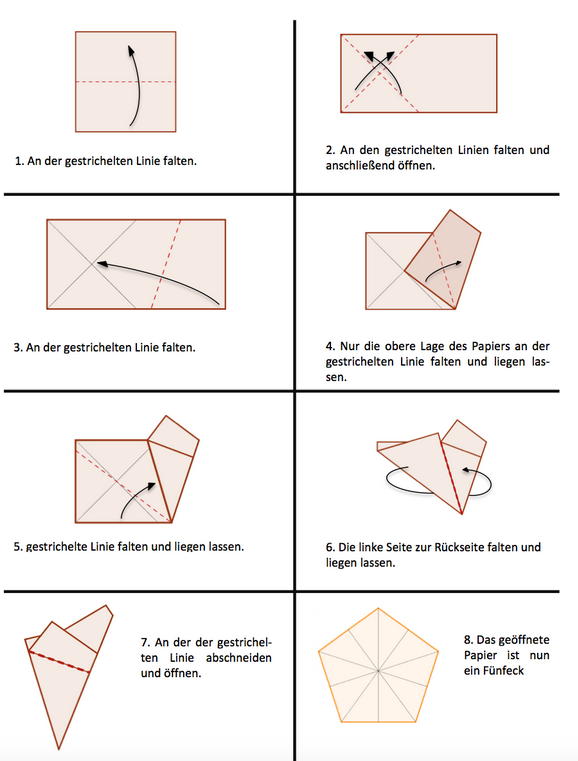
Fertigen Sie ausgehend von der Faltanleitung eine DGS-Konstruktion an.
Zeigen Sie mit Hilfe dieser DGS-Konstruktion, dass die Faltanleitung kein regelmäßiges Fünfeck liefern kann und begründen Sie dies kurz.
Quellenangabe:
- Lösung
- Themengebiet
- Geförderte Kompetenzen
- Heurismen
- Schwierigkeitsgrad
- Umsetzung im Mathematikunterricht
- Einsatzmöglichkeiten
Schritt 1:
Nach dem ersten Falten (Schritt 1, s.o.) des Quadrates erhält man ein Rechteck. In der DGS kann hierfür direkt ein Rechteck mit den nötigen Seitenverhältnissen – die langen Seiten sind doppelt so lang wie die kurzen – konstruiert werden:

Schritt 2:
Im nächsten Schritt kann man, z. B. über die Mittelsenkrechten-Funktion, das Rechteck in zwei kongruente Quadrate teilen. Über das Verbinden der schräg gegenüberliegenden Eckpunkte des linken Quadrates erhält man dessen Diagonalen. Ihr Schnittpunkt liefert den für die in Schritt 3 auszuführende Faltung notwendigen Punkt.
Schritt 3:
Auf den eben beschriebenen Punkt soll nun die untere rechte Ecke des Rechtecks, Punkt B, gefaltet werden. Für diese Faltung muss zunächst die Faltgerade konstruiert werden. Diese erhält man, indem man den zuvor erwähnten Diagonalenschnittpunkt (in der folgenden Abbildung als Punkt B’ bezeichnet) über eine Strecke mit Punkt B verbindet und anschließend zu dieser die Mittelsenkrechte konstruiert. Diese Mittelsenkrechte teilt das Rechteck in zwei Teilvierecke. Spiegelt man das rechte Teilviereck (BGJ’L’) an der Mittelsenkrechten, erhält man schließlich die in Schritt 3 geforderte Faltung (siehe Abb. 3).

Schritt 4:
Für die nächste Faltung konstruiert man die Winkelhalbierende des Winkels ∢ B’L’J’. Anschließend spiegelt man an dieser das Dreieck L’RB’ (siehe Abb. 4).

Schritt 5:
Schließich konstruiert man eine Gerade durch L’ und B’ und spiegelt das sich damit ergebende Dreieck AL’S an eben dieser Geraden (siehe Abb. 5).

Blendet man alle Elemente aus, die „weggefaltet“ wurden, erhält man die folgende Darstellung:

Auf den letzten Teil, der ein Schneiden und Ausfalten beinhaltet, soll an dieser Stelle verzichtet werden, da mit den vorausgegangenen Schritten eindeutig begründet werden kann, dass sich aus dieser Faltanleitung kein regelmäßiges Fünfeck ergeben kann.
Begründung der Unregelmäßigkeit
Bereits bei dem Erstellen der Konstruktion fallen Abweichungen zu der Darstellung in der Faltanleitung sofort ins Auge. So muss man bemerken, dass Punkt R nicht auf der Rechteckseite (Seite EG) liegt (siehe Abb. 5), obwohl dies laut Faltanleitung gefordert wird.
Um die sich aus diesen Abweichungen ergebende Vermutung, dass sich am Ende kein regelmäßiges Fünfeck ergibt, zu bestätigen, sollte die DGS-Konstruktion genauer betrachtet werden. Tut man dies, lässt sich erkennen, dass man mit der Anleitung nicht die für ein Fünfeck erforderliche Innenwinkelsumme von 540° erhält. Beim genaueren Analysieren der Vorgehensweise kann man erkennen, dass der Fehler auf einer Fehlannahme aus dem 3. Schritt beruht. Die hierbei getätigte Faltung liefert nicht die für die Konstruktion erforderlichen Winkelgrößen, sondern bringt leichte Abweichungen davon mit sich (siehe Abb. 7).
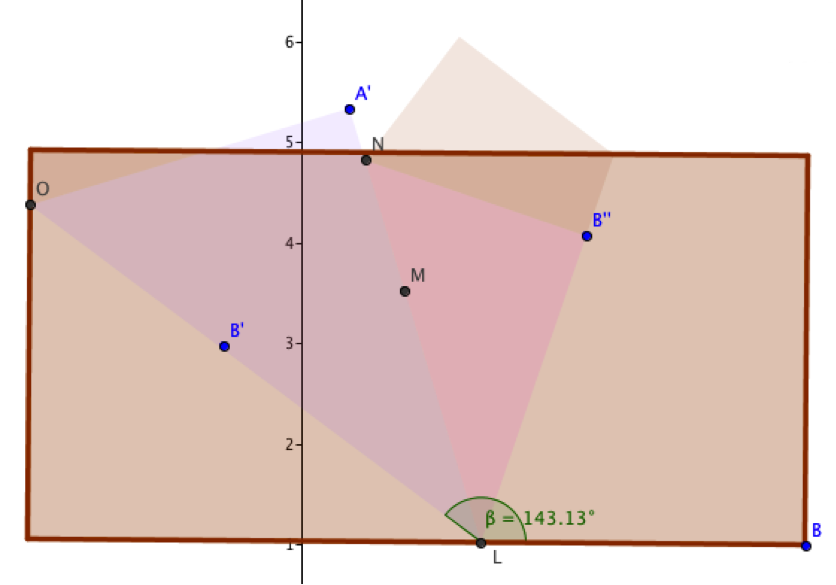
Der in der Abbildung eingetragene Winkel Beta müsste für die Faltung eines regelmäßigen Fünfecks 144° betragen, da dieser die Summe von vier der in der folgenden Abbildung dargestellten 36°-Winkel bildet (siehe Abb. 8).

„Sie entdecken Eigenschaften und Beziehungen und lernen sie zu begründen. Das Entdecken und Erkunden von Eigenschaften ebener Figuren werden durch den Einsatz von dynamischer Geometriesoftware gefördert. Dazu gehören u. a. die besonderen Linien im Dreieck und die Eigenschaften von Vierecken.“2
„Die Schülerinnen und Schüler erkunden Beziehungen zwischen geometrischen Figuren, verstehen wesentliche Sätze und wenden diese zur Lösung von inner- und außermathematischen Problemen an.“4
Da jedoch hier eine Vielzahl bzw. Aneinanderreihung von geometrischen Abbildungen zur Lösung erforderlich sowie der geübte Umgang damit und ein gewisses Maß an kognitiventlastender Routine nötig ist, sollte diese Aufgabe nicht etwa in den Klassenstufen 7/8 angesiedelt werden, sondern vielmehr ist es zu empfehlen, diese in der 9. oder 10. Klasse zu behandeln.
2 Ministerium für Bildung, Jugend und Sport des Landes Brandenburg (2008): Rahmenlehrplan für die Sekundarstufe I. Jahrgangsstufen 7 – 10. Mathematik. 1. Auflage, o.O, S. 38
3 Ministerium für Bildung, Jugend und Sport des Landes Brandenburg (2008): Rahmenlehrplan für die Sekundarstufe I. Jahrgangsstufen 7 – 10. Mathematik. 1. Auflage, o.O, S. 38
4 Ministerium für Bildung, Jugend und Sport des Landes Brandenburg (2008): Rahmenlehrplan für die Sekundarstufe I. Jahrgangsstufen 7 – 10. Mathematik. 1. Auflage, o.O, S. 38
Durch ihre Komplexität und vielschichtigen Anforderungen fördert diese Aufgabe eine Vielzahl an fachbezogenen Kompetenzen. Dies gilt sowohl für prozessbezogene als auch für inhaltsbezogene mathematische Kompetenzen.
- Prozessbezogene mathematische Kompetenzen:
Argumentieren:
In der vorliegenden Aufgabe muss die gegebene Faltanleitung analysiert und verstanden werden. Beim Entwickeln eines Plans zur Lösung des Problems können bereits erste Vermutungen darüber angestellt werden, warum kein regelmäßiges Fünfeck entstehen kann.
Zur vollständigen Bewältigung des Problems muss schließlich logisch nachvollziehbar begründet werden, warum die Faltanleitung an der Konstruktion eines regelmäßigen Fünfecks scheitert. Beim Argumentieren müssen die SuS auf die in der bzw. den Figuren vorliegenden geometrischen Beziehungen zurückgreifen.
Probleme lösen:
Die SuS müssen in der Aufgabe Strategien und Werkzeuge für die geeignete 'Übersetzung' in bzw. Erweiterung zu DGS-Konstruktionen anwenden. Die gegebene Faltanleitung ist also kein vorgegebenes Lösungsverfahren, sondern die SuS müssen ihren individuellen Weg zur Lösung des Problems finden und können dabei ganz unterschiedlich vorgehen. Die verschiedenen Lösungswege beziehen sich sowohl auf die Bearbeitung der Aufgabe in einem DGS-System, als auch auf die verschiedenen mathematischen Lösungsansätze zur Erklärung der Tatsache, dass kein regelmäßiges Fünfeck entstanden ist. Gerade bei der Präsentation der mathematischen Lösung sind verschiedene Darstellungsformen notwendig die von der Art der jeweiligen Lösung abhängen (eine grafische Lösung muss anders präsentiert werden als eine algebraische Lösung usw.) und somit Raum für Diskussionen zwischen den SuS auf inhaltlicher und formaler Ebene lassen. Auf diese Weise wird das Reflektieren von Lösungswegen, Strategien und formaler Darstellungen mathematischer Inhalte gefördert.
Darstellungen verwenden:
Bei der vorliegenden Aufgabe müssen die Schüler zwischen verschiedenen Darstellungsformen der Mathematik wechseln und dadurch mit ihnen umgehen lernen. Sie starten mit einem geschriebenen Text den sie grafisch in einem DGS umsetzen müssen, wobei sie sich geometrischer Werkzeuge bedienen. Anschließend gilt es anhand der grafischen Umsetzung das zugrundeliegende mathematische Problem zu erkennen und dies in eine formale, mathematisch-symbolische Form zu transferieren. Dies verlangt von den SuS das Interpretieren, Auswählen und Anlegen solcher unterschiedlichen Darstellungsformen und stärkt somit einen flexiblen, problemangemessenen Umgang mit diesen.
Kommunizieren:
Schon für die Lösung und Präsentation der Aufgabe ist ein intensiver Kommunikationsprozess innerhalb der Klasse notwendig. Zunächst müssen sich die SuS über verschiedene Strategien und Lösungsansätze austauschen und diese dann praktisch umsetzen. Dabei findet eine Kommunikation über mathematische Zusammenhänge und Inhalte in einer relativ natürlichen Sprache statt, da die SuS sich erst einmal der Lösung annähern müssen und hier ein zu formales Vorgehen den meisten im Weg stehen würde. Teil des mathematischen Kommunizierens ist es aber auch sich in einer angemessenen Fachsprache ausdrücken zu können und die gewonnen Erkenntnisse in geeigneter Form zu dokumentieren und zu präsentieren. Diese Ebene wird durch den zweiten Teil der Aufgabe, der Begründung warum kein regelmäßiges Fünfeck entsteht, und der anschließenden Reflektion des Vorgehens abgedeckt. Damit ist die Sprache das „zentrale Verständigungsmittel“ welches die gemeinschaftliche Zusammenarbeit und Bearbeitung der Aufgabe ermöglicht.
- Inhaltsbezogene mathematische Kompetenzen:
Raum und Form:
Durch die DGS-Konstruktion der Faltanleitung lernen die SuS den Umgang mit verschiedenen geometrischen Figuren und Strukturen. Sie müssen selbständig ein mathematisches Problem in die Sprache der Geometrie übersetzten. Anschließend gilt es die Konstruktion analytisch zu bearbeiten und sich so „dem Fehler“ in der Faltanleitung anzunähern. Schließlich können sie ihre Lösung nur präsentieren, wenn sie die Eigenschaften und Beziehungen zwischen den verschiedenen geometrischen Figuren durchschauen, beschreiben und den Fehler logisch darlegen können.
- Die DGS funktioniert als zentrale Arbeitsplattform für die Bearbeitung dieser Aufgabe. Durch das Anfertigen der DGS-Konstruktion wird der Schüler dazu angehalten, die vorliegende Faltanleitung zu mathematisieren und selbstständig zu formalisieren.
- Die DGS-Konstruktion ermöglicht es ihm, die mathematische Komplexität dieser Anleitung zu bewältigen, sie schrittweise nachzuvollziehen, mathematisch zu interpretieren und genauer zu analysieren.
- Im ersten Teil der Aufgabe, dem Umsetzen der Faltanleitung innerhalb der DGS, erscheint das Vorwärtsarbeiten als sinnvoll, da die Anleitung Schritt für Schritt abgearbeitet werden kann.
- Bei der Begründung kann ebenfalls vorwärtsgearbeitet werden, indem vom ersten Schritt ausgehend jede einzelne Faltung mithilfe der DGS analysiert und mathematisch hinterfragt wird. Jedoch ist es hierbei auch vorstellbar, von dem letzten Schritt bzw. dem Fünfeck aus die Anleitung rückwärts durchzugehen und genauer zu betrachten.
- Grundsätzlich bietet sich ein kombiniertes Vorwärts- und Rückwärtsarbeiten an, um die Probleme, die diese Faltanleitung aufwirft, näher zu bestimmen und den eigentlichen „Knackpunkt“ zu erkennen.
- Falls Schwierigkeiten bei der Lösungsfindung auftreten, kann bei dieser Aufgabe auch ein systematisches Probieren innerhalb der DGS auch hilfreich sein.
- Da vor allem beim zweiten Teil der Aufgabe eine Vielzahl von individuellen Lösungswegen möglich und auch zu erwarten sind, können verschiedene heuristische Prinzipien zum Einsatz kommen.
- So ist es für die Entwicklung einer Begründung, weshalb es sich bei dem Faltergebnis um kein regelmäßiges Fünfeck handelt, beispielsweise ein Zerlegen oder Ergänzen der einzelnen Figuren, die man in den Arbeitsschritten erhält, sehr hilfreich (z.B. um zu zeigen, dass sich nicht die nötige Innenwinkelsumme ergibt (s.o.)).
Da dieser Aufgabe 4 Punkte vergeben wurden, wurde diese Aufgabe mit ** gekennzeichnet. Hier die Analyse:
Die Aufgabe ist sprachlich sehr einfach und klar formuliert und die Arbeitsschritte werden in ihrer Abfolge sprachlogisch leicht verständlich dargeboten.Die sprachlogische Komplexität entspricht der Stufe 0.
Bei der vorgestellten Aufgabe gibt es keinen festvorgegebenen Lösungsweg. Die Konstruktion sowie die Begründung können auf sehr unterschiedliche Weise vorgenommen werden.Für beide Teile sind diverse geometrische Beziehungen und Nebenbedingungen zu berücksichtigen und verschiedene heuristische Strategien anzuwenden.Es wird damit deutlich, dass die kognitive Komplexität auf der Stufe 2 liegt.
In der beschriebenen Aufgabe beinhaltet das Formalisieren ein mathematisches Erfassen und „Übersetzen“ einer „Bastelanleitung“ in geometrische Objekte und Abbildungen. Diese Formalisierung ist in keiner Art und Weise vorgegeben, sondern muss von Grund auf selbstständig erarbeitet werden. In gleicherweise ist die Begründung (dass es sich nicht um ein regelmäßiges Fünfeck handelt) mathematisch formalisiert darzustellen. Die Aufgabe ist hinsichtlich der Formalisierung von Wissen in der Stufe 2 einzuordnen.
Auf der algebraischen Ebene sind in dieser Aufgabe lediglich verschiedene Winkelgrößen zu berechnen und zu vergleichen. Diese lassen sich sogar automatisch über die DGS ausgeben. Folglich liegt hier die Formelhandhabung in ihrer Komplexität auf der Stufe 0.
Grundsätzlich lässt sich das Bewätigen einer mathematischen Problemlöseaufgabe (nach George Pólya) in vier Schritten vollziehen. Als basalste (allgemein-strategische) Hilfestellung kann den SuS diese (im Folgenden dargestellte) Schrittfolge vorgegeben werden, um ihnen ein erstes Grundgerüst zum mathematischen Problemlösen bereitzustellen.
Im ersten Schritt geht es um das Verstehen und Analysieren der Aufgabe. Hier bieten sich insbesondere für unsere Aufgabe die folgenden Hilfestellungen an:
| Allgemein-strategische Hilfe | Inhaltlich-strategische Hilfe |
| Sieh dir die Faltanleitung an. Nimm dir ein Blatt Papier und versuche sie zunächst ohne DGS daran nachzuvollziehen. | Welche Figur entsteht? Bist du dir sicher, dass es sich um ein regelmäßiges Vieleck handelt? |
| Kannst du auf diese Weise exakt arbeiten und auch durch einfaches Falten und Messen mit Papier und Lineal genau begründen? Bietet dir eine DGS hierfür Vorteile? |
Der zweite Schritt beinhaltet das Ausdenken eines Plans bzw. einer Lösungsstrategie während der dritte Part dann die Ausführung des Plans enthält. Für beide Teile bieten sich für unsere Aufgabe je nach Bedarf Hilfestellungen auf unterschiedlichen Ebenen an. Grundsätzlich sind zunächst immer erst allgemein-strategische Hilfestellungen zu wählen. Inhaltiche Hilfestellungen sollte in der Regel erst, wenn allgemein-strategische und inhaltich-strategische Hilfestellungen den SuS nicht weiterhelfen konnten, eingesetzt werden:
| Allgemein-strategische Hilfen | Inhaltlich-strategische Hilfen | Inhaltliche Hilfen |
| Wie lässt sich diese Aufgabe am besten in eine DGS übertragen? Welche geometrischen „Werkzeuge“, die du bereits kennengelernt hast, könnten dir dabei helfen? | Bei der Visualisierung der Faltanleitung anhand einer DGS hast du verschiedene Möglichkeiten. Eine Variante wäre, dass du dir überlegst, wie sich eine Faltung geometrisch darstellen lässt. Was passiert aus mathematisch-geometrisch Sicht, wenn du ein Blatt in der Mitte faltest? | Mathematische Werkzeuge, die dir bei der Erstellung der Faltanleitung mit einer DGS helfen könnten, sind u. a. die Winkelhalbierende, Spiegelungen und die Mittelsenkrechte. |
| Überlege dir, wie du die Aufgabe angehen willst, da es viele unterschiedliche Wege gibt, sie zu lösen. Du kannst beispielswiese zunächst eine DGS-Konstruktion erstellen und durch Probieren herausfinden, warum kein regelmäßiges Fünfeck entsteht. | Eine andere Möglichkeit wäre sich im Voraus Gedanken zu machen, was an der Faltanleitung „falsch“ sein könnte, um dann gezielt bei der Erstellung der DGS-Konstruktion darauf zu achten, ob sich deine Hypothese bestätigen lässt. Dies sind nur zwei mögliche Strategien, du kannst natürlich auch anders vorgehen. | Bei der Begründung, dass bei dem Faltvorgang kein regelmäßiges Fünfeck entsteht, lohnt es sich, über die Winkelsumme des Fünfeckes und über die Größe eines einzelnen Winkels eines regelmäßigen Fünfecks nachzudenken. |
|
Weitere Fragen, über die es sich lohnt nachzudenken, sind:
|
Beim Durchlaufen dieser vier Stationen ist es wichtig, den SuS - bezogen auf das individuelle Leistungsniveau, und auf persönliche Schwäche sowie Stärken - möglichst angemessene Hilfestellungen bereitzustellen. Dabei sollten diese auf das für ein Weiterkommen Notwendigste reduziert werden, um trotzdem ein möglichst hohen Grad an Selbstständigkeit in der unterrichtlichen Arbeit der SuS zu wahren.
Die hier vorgeschlagenen Hilfestellungen stellen nur eine kleine Auswahl von vielen Möglichkeiten dar, die selbstverständlich ergänzt werden können.
Bei der Umsetzung der Aufgabe im Unterricht sind verschiedene Sozialformen denkbar. Grundsätzlich kann die Aufgabe in Einzelarbeit gelöst werden. Auch denkbar wäre eine Partnerarbeit bei der zwei SuS sich gemeinsam beraten können. Jedoch sollte hierbei trotzdem jeder an einem eigenen Computer arbeiten, da bei der Arbeit am PC schnell eine der beiden Personen nur zum Zuschauer wird. Aus diesem Grund sollte insbesondere von einer 'Gruppenarbeit von Anfang an' bei dieser Aufgabe abgesehen werden.
Deutlich effektiver als eine einfache Einzelarbeit kann ein Unterricht nach dem Ich-Du-Wir-Prinzip sein. Hierbei starten die SuS in Einzelarbeit - jeder an einem eigenen Computer -, machen sich mit der Aufgabe vertraut und sammeln selbstständig erste Ideen und Lösungsansätze. Im Anschluss gehen sie über in die Partnerarbeit, in der sie sich austauschen und sich gegenseitig die gesammelten Erfahrungen, Ideen oder Lösungswege vorstellen. Nach dieser Phase finden sich dann die SuS in Gruppen zusammen und besprechen ihre Resultate, um anschließend ihre Lösungen vor der Klasse zu präsentieren.
Abschließend und unabhängig von der Sozialform sollte die Aufgabe mit der gesamten Klasse besprochen werden, um sicherzustellen, dass am Ende jeder einen möglichen Lösungsweg kennt und die Problematik verstanden hat. Außerdem sollte darauf geachtet werden, dass eine Ergebnissicherung stattfindet. Die gesammelten Erkenntnisse sollten dabei im Hefter handschriftlich festgehalten werden, damit diese auch nach der Arbeit am Computer zur Verfügung stehen.
Hinweise für die Leistungsschwächeren Schülerinnen und Schüler
Für leistungsschwächere Schüler könnte man eine Faltanleitung für eine DGS-Konstruktion, wie etwa die von uns oben beschriebe Anleitung, vorbereiten, um ihnen einen ersten Ausgangspunkt für Formalisierungen und Beispiele bzw. Vorlagen für den Umgang mit einer solchen Anleitung anzubieten. Wenn man die Faltanleitung nicht als Ganzes verteilt, sondern immer nur schrittweise herausgibt werden sehr gezielte und differenzierte Hilfestellungen möglich die den Schülern nur eine Lösung für das jeweils aktuelle Problem anbieten, ohne aber schon die gesamte Konstruktion zu verraten.
Sollten Schüler bei der technischen Umsetzung Schwierigkeiten haben, könnte die DGS-Konstruktion vorgeben werden. Diese müssen sie dann nachvollziehen und nachkonstruieren. Auch hier ist es möglich, wieder nur Teile der Hilfestellungen anzubieten und so anschließend ein selbständiges Arbeiten zu ermöglichen. So werden etwa in den ersten Konstruktionsschritten wesentliche Konzepte für die Aufgabe, wie Mittelsenkrecht, Winkelhalbierende oder das Konstruieren eines Quadratmittelpunktes, bereits vorgestellt und stehen damit als Werkzeug für das weitere Vorgehen zur Verfügung. Diese teilweise vorgegeben DGS-Konstruktion gibt den Schülern somit einen ersten Ausgangspunkt für Formalisierungen und Beispiele bzw. Vorlagen für den Umgang mit einer Faltanleitung.
Bei all diesen Hilfestellungen ist jedoch noch nicht das zugrunde liegende mathematische Problem berührt worden, was somit also auch noch eine inhaltlich-strategische bzw. inhaltliche Differenzierung ermöglicht. Wie sich eine Differenzierung auf dieser Ebene gestalten kann ist bereits unter dem Punkt inhaltliche Hilfen angesprochen worden.
Hinweise für die Leistungsstärkeren Schülerinnen und Schüler
Leistungstärkeren Schülern kann man gerecht werden, indem man möglichst wenig vorgibt und sie weitestgehend selbstständig das Problem bewältigen lässt, da sich die Aufgabe auf Grund ihrer kognitiven Komplexität (s.o.) und der notwendigen (selbstständigen) Formalisierungsleistung auf diese Weise sehr anspruchsvoll gestaltet.
Es zeigt sich also, dass durch Variation der Art und des Umfangs der Hilfestellungen und in Abhängigkeit davon, wie viel man vorgeben möchte, die Aufgabe sehr differenziert im Unterricht eingesetzt werden kann. Einerseits stellt die Aufgabe also auf Grund ihres recht hohen Schwierigkeitgrads eine Herausforderung für leistungsstarke Schüler dar, während andererseits über adäquate Lernhilfen, die sich besonders innerhalb der DGS sehr vielseitig gestalten lassen, auch weniger leistungsstarke Schüler diese Aufgabe als bewältigbare Herausforderung sowie Lernchance wahrnehmen und lösen können.
Diese Aufgabe berührt verschiedene (schul-)mathematische Bereiche. Sie kann besonders gut im Kontext der Beschäftigung mit geometrischen Figuren bzw. Objekten und ihren Beziehungen eingesetzt werden. Schüler sollten hierfür bereits Objekte wie Winkelhalbierende, Mittelsenkrechte, Fünfecke sowie geometrische Abbildungen wie Geradenspiegelungen (und evtl. Drehungen) kennen. Außerdem erfordert die Bearbeitung der Aufgabe auch Kenntnisse im Umgang mit DGS und das nötige Wissen, um hierin mit den angeführten Objekten und Abbildungen eigene Konstruktionen anfertigen zu können.
Die Bearbeitung dieser Aufgabe fördert das Verstehen von geometrischen Objekten und ihren Relationen. Außerdem müssen die SuS eigene Argumentationstrukturen und 'Beweisstrukturen' entwickeln, um damit ihre Festellungen logisch und nachvollziehbar zu begründen.
Denkbar wäre auch diese Aufgabe als Teil einer größen Projektarbeit, in der verschiedene Probleme mit Hilfe von DGS bearbeitet werden, einzusetzen. Werden hierbei von verschiedenen Gruppen unterschiedliche Aufgaben bearbeitet, eignet sich diese Aufgabe für etwas leistungsstärkere SuS bzw. Gruppen.
Grundvoraussetzung für die Bearbeitung dieser Aufgabe ist die Verfügbarkeit einer ausreichenden Anzahl an Computer mit einer dynamischen Geometrie-Software, um den Schülern ein selbstständiges Arbeiten zu ermöglichen.
Bearbeitet von: David Meyer-Belitz, Chris Lindner & Ana Kuzle
Feedback
Wir freuen uns auf Ihre Anregungen und konstruktive Rückmeldung zum Material.
Copyright © 2014-2017 - Ana Kuzle
