Argumentieren am Zahlengitter

Fehlermeldung

Deprecated function: The each() function is deprecated. This message will be suppressed on further calls in FieldCollectionItemEntity->fetchHostDetails() (Zeile 313 von /www/htdocs/w0127817/beta.proffi-m.de/sites/all/modules/field_collection/field_collection.entity.inc).
Klasse Schulstufe Thema Themengebiet Schwierigkeit
3/ 4 Primarstufe Produktive Übungen im ZR 100 Zahlen und Operationen *

Aufgabenstellung


Im oberen linken Feld steht die Startzahl (hier 3). Die noch leeren Kästchen werden fortlaufend ausgefüllt, indem in der Waagerechten bzw. Senkrechten vorgeschriebene Zahlen addiert werden, weshalb diese Zahlen im Weiteren als Pluszahlen bezeichnet werden (zusammen können sie als Pluszahl-Paar betitelt werden). Die untere rechte Zahl wird Zielzahl genannt, die Zahl in der Mitte Mittelzahl und die übrigen werden als Randzahlen bezeichnet.
 
                                                                            a) Fülle zunächst das Zahlengitter aus.
                                                                            b) Was ändert sich, wenn man die Pluszahlen verändert?
                                                                            c) Kannst du mit anderen Pluszahlen zu derselben Zielzahl wie in a) gelangen?
                                                                            d) Wie viele Möglichkeiten gibt es, um zu dieser Zielzahl zu gelangen?
                                                                            e) Was fällt dir auf? Welcher Zusammenhang besteht zwischen den besonderen
                                                                                Zahlen: Startzahl - Mittelzahl - Zielzahl? Welcher besondere Zusammenhang
                                                                                ergibt sich für die Startzahl 0?
                                                                             f) Erfinde ein Zahlengitter mit der Zielzahl 25.
 

Quellenangabe:

In Anlehnung an SELTER (2004)


Lösungsvariante 1

a) Fülle zunächst das Zahlengitter aus.
 
 
b) Was ändert sich, wenn man die Pluszahlen verändert?
 
Vertauscht man die Pluszahlen, so finden sich alle Zahlen, die vorher in der ersten Spalte standen, nun in der ersten Zeile wieder. Ebenso tauchen die Zahlen aus der zweiten bzw. dritten Spalte nun in der zweiten bzw. dritten Zeile auf. Man kann auch sagen, dass die Werte des Zahlengitters an der Diagonalen gespiegelt wurden. Verändert man nur eine der zwei Pluszahlen, zum Beispiel die waagerechte Pluszahl, dann ändern sich die Werte aus der ersten Spalte des Zahlengitters nicht, jedoch alle übrigen. Vergrößert bzw. vermindert man beide Pluszahlen gleichmäßig, so verändern sich sämtliche Kästchen des Zahlengitters und somit auch die Mittelzahl und Zielzahl. Vergrößert man eine der Zahlen um eins und verringert die andere um eins, so ändern sich zwar einige Werte in den Kästchen, jedoch bleiben Mittelzahl und Zielzahl gleich.
 

c) Kannst du mit anderen Pluszahlen zu derselben Zielzahl wie in a) gelangen?
 
Ja, beispielsweise mit den Zahlen 5 und 6.
 
 
d) Wie viele Möglichkeiten gibt es, um zu dieser Zielzahl zu gelangen?

Gesucht sind weitere Möglichkeiten, die Zielzahl 25 mit vorgegebener Startzahl 3 zu erreichen. Von der Startzahl zur Zielzahl addiert man zweimal die waagerechte Pluszahl und ebenso zweimal die senkrechte Pluszahl. Somit müssen die beiden gesuchten Zahlen in der Summe, die Hälfte der Differenz der Zahlen 3 und 25 ergeben. Die Differenz von 3 und 25 beträgt 22. Die beiden Pluszahlen müssen zusammen also 11 ergeben. Damit lassen sich folgende Möglichkeiten an Pluszahl-Paaren ausmachen: 0 und 11; 1 und 10; 2 und 9; 3 und 8; 4 und 7; 5 und 6. Je nachdem, ob die Zahl als waagerechte bzw. als senkrechte Pluszahl gewählt wird, kann man die Zahlen auch noch vertauschen. Insgesamt ergeben sich somit 12 Möglichkeiten.
Gibt es noch weitere Möglichkeiten? Nein, es kann keine weiteren Möglichkeiten mehr geben, da systematisch eine Zahl um eins verringert und die andere Zahl um eins vergrößert wurde. Alle weiteren Summen zweier natürlicher Zahlen ergeben mehr bzw. weniger als 11.
 
 
e) Was fällt dir auf? Welcher Zusammenhang besteht zwischen den besonderen Zahlen: Startzahl - Mittelzahl -
    Zielzahl? Welcher besondere Zusammenhang ergibt sich für die Startzahl 0?
 
Die Mittelzahl stellt die Summe aus der Startzahl und den beiden Pluszahlen dar. Die Zielzahl kann dann als Summe der Mittelzahl zuzüglich der beiden Pluszahlen betrachtet werden. Anders kann die Zielzahl aber auch von der Startzahl aus gedacht, als die Summe von dem Doppelten der Pluszahlen und der Startzahl verstanden werden. Ist die Startzahl 0, so ist die Mittelzahl die Summe der waagerechten und senkrechten Pluszahlen und die Zielzahl ist dann das Doppelte der Mittelzahl.
 
 
f) Erfinde ein Zahlengitter mit der Zielzahl 23.
 
In Anlehnung an das gegebene Zahlengitter verringert sich die Zielzahl um zwei. In Teil e) wurde herausgearbeitet, dass die Zielzahl die Summe von Startzahl und dem Doppelten der beiden Pluszahlen darstellt. Wenn sich nun die Zielzahl um den Wert zwei verringert, kann dies durch eine andere Startzahl oder durch eine Änderung des Pluszahl-Paares bedingt werden. Nehmen wir an, die Pluszahlen bleiben gleich. Dann muss die Startzahl verändert werden, nämlich, ebenso wie die Zielzahl um den Wert 2 verringert werden. In diesem Fall kann die Startzahl demnach von 3 auf 1 herabgesetzt werden. Betrachten wir nun den anderen Fall, also eine Veränderung der Pluszahlen. Damit die Zielzahl um zwei kleiner wird, muss die Summe des Pluszahl-Paares insgesamt um eins gesenkt werden, denn das Pluszahl-Paar wirkt sich ja zweifach auf die Zielzahl aus. Hieraus ergeben sich viele Lösungsmöglichkeiten, eine wäre das Pluszahl-Paar 4 und 6.
 
 
 
 
Lösungsvariante 2

a) Fülle zunächst das Zahlengitter aus.

Ein möglicher alternativer Lösungsweg der Aufgabe führt zu keinem anderen Ergebnis. Das ausgefüllte Zahlengitter wird, bei korrektem Ausfüllen, immer die Werte aus dem zuerst beschriebenen Lösungsweg haben. Unterschiede im Lösungsweg sind bei diesem Aufgabenteil lediglich in der Hinsicht möglich, wie bzw. in welcher Reihenfolge das Zahlengitter ausgefüllt wird. „Die »Zielzahl« des Zahlengitters kann auf beliebigen »Gitterwegen« in vier Rechenschritten erreicht werden (z.B. zweimal waagerecht und zweimal senkrecht oder einmal waagrecht, zweimal senkrecht und einmal waagrecht). Das Kommutativgesetz \((a+b=b+a)\), Assoziativgesetz \(((a+b)+c=a+(b+c)) \) und das Distributivgesetz (hier:\(2⋅(a+b)=2⋅a+2⋅b)\)) bzgl. der Addition kommt zum Tragen“ (BEZOLD, 2010b, S.14).

 

b) Was ändert sich, wenn man die Pluszahlen verändert?

Antworten auf diesen Aufgabenteil werden hinsichtlich Umfang und Genauigkeit stark variieren. Es können also solche Antworten erwartet werden, die nur die Veränderung einer Pluszahl oder die beider Pluszahlen beschreiben.

 

c) Kannst du mit anderen Pluszahlen zu derselben Zielzahl wie in a) gelangen?

Wurde eine Entdeckung bezüglich der Kombinationsmöglichkeiten aus Pluszahlen noch nicht in Teil b) erkannt, wird sie mittels dieser Aufgabenstellung provoziert. Bei der Beantwortung genügt es, ein Beispiel anzugeben, denn die Frage nach allen Möglichkeiten wird nicht gestellt. Dennoch ist zu erwarten, dass einige Schülerinnen und Schüler versuchen, mehrere Möglichkeiten zu finden.

 

d) Wie viele Möglichkeiten gibt es, um zu dieser Zielzahl zu gelangen?
 
Spätestens mit dieser Frage wird die Suche nach allen Möglichkeiten angestoßen. Neben der Angabe aller Möglichkeiten wird zudem eine Begründung gefordert, warum alle Lösungen gefunden wurden und es darüber hinaus keine weiteren Lösungen mehr geben kann. Geht man bei der Angabe aller Möglichkeiten systematisch vor, wie in dem aufgezeigten Lösungsweg, so lässt sich daraus einfacher eine plausible Begründung ableiten, als wenn durch bloßes Probieren viele Lösungen nebeneinanderstehen.
 

e) Was fällt dir auf? Welcher Zusammenhang besteht zwischen den besonderen Zahlen: Startzahl - Mittelzahl -   
    Zielzahl? Welcher besondere Zusammenhang ergibt sich für die Startzahl 0?

Bei dieser Aufgabenstellung kann es dazu kommen, dass Schülerinnen und Schülern das Entdecken der gesuchten Zusammenhänge sehr schwer fällt. Manchen mag es einfacher gelingen, Zusammenhänge mit der Startzahl 0 zu entdecken, Anderen mit einer von 0 abweichenden Startzahl. Dennoch sollte bewusst darauf geachtet werden, dass die beschriebenen Erkenntnisse, wie im ersten Lösungsweg, erkannt werden.
 

f) Erfinde ein Zahlengitter mit der Zielzahl 23.

Diese Aufgabe stellt den Aufgabentyp „Umkehraufgabe“ (Bruder, 2005) dar, denn die Zielzahl ist vorgegeben und die Umformungen die dahin führen sind bis auf die genaue Angabe von Pluszahlen bekannt. Aus den gewonnenen Erkenntnissen aus Teilaufgabe e) kann gefolgert werden, dass mit der Startzahl 0 die Zielzahl 23 nicht gefunden werden kann. Dies gilt insbesondere für alle geraden Startzahlen. Denn die waagerechte und senkrechte Pluszahl werden insgesamt je zweimal auf die Startzahl addiert. Sind die beiden Pluszahlen gerade, so ist bei gerader Anfangszahl auch die Zielzahl gerade. Für den Fall, das beide Pluszahlen ungerade sind, ergeben diese in der Summe eine gerade Zahl. Somit sind bei gerader Startzahl in diesem Fall auch die Mittelzahl und Zielzahl gerade. Zuletzt kann man den Fall für eine ungerade und eine gerade Pluszahl betrachten. Somit ist die Summe der Pluszahlen ungerade. Ist in diesem Fall die Startzahl gerade, so ist die Mittelzahl nun ungerade. Da die Zielzahl allerdings die Summe von Startzahl und dem zweimaligen Addieren der Pluszahlen darstellt, ist sie auch in diesem Fall wieder gerade.
Zur Übersicht zeigt folgende Tabelle alle möglichen Fälle, wobei Pluszahl 1 und 2 als waagerechte bzw. senkrechte Pluszahl gedeutet und vertauscht werden können, jedoch keine Veränderungen der Eigenschaften von Mittelzahl und Zielzahl liefern:
 

Startzahl Pluszahl 1 Pluszahl 2 Mittelzahl Zielzahl
Gerade Gerade Gerade Gerade Gerade
Ungerade Gerade Gerade Ungerade Ungerade
Gerade Ungerade Ungerade Gerade Gerade
Ungerade Ungerade Ungerade Ungerade Ungerade
Gerade Gerade Ungerade Ungerade Gerade
Ungerade
 Gerade Ungerade Gerade Ungerade
 
Tab. 2.1: Zusammenhang der Zahlen Startzahl-Mittelzahl-Zielzahl in Abhängigkeit der Wahl einer geraden/ungeraden Startzahl und der Wahl
               gerader/ungerader Pluszahlen
 
Für die Suche nach einem Zahlengitter mit der Zielzahl 23 folgt also, dass keine gerade Startzahl gewählt werden kann. Aus Teil e) folgte, dass die Mittelzahl die Summe aus Startzahl, der waagerechten Pluszahl und der senkrechten Pluszahl darstellt und die Zielzahl somit als Summe von Startzahl zuzüglich dem Doppelten des Pluszahl-Paares angesehen werden kann. Nimmt man nun eine beliebige ungerade Startzahl, so muss anschließend die Differenz zwischen gewählter Startzahl und der Zielzahl 23 bestimmt werden. Die Hälfte der ermittelten Differenz ist dann die Summe der Pluszahlen, woraus sich wiederrum mehrere Kombinationsmöglichkeiten ergeben. Sind diese Zusammenhänge erst erschlossen, ist es leicht, alle in Frage kommenden Zahlengitter zu suchen. Folgende Tabelle veranschaulicht die Abhängigkeit der gewählten Startzahl zu den in Frage kommenden Pluszahlen an möglichen Pluszahl-Paaren:
 
Startzahl Differenz zwischen gewählter Startzahl und Zielzahl (23) Bei gewählter Startzahl ergeben die Pluszahlen in der Summe: Bei gewählter Startzahl kommen folgende Pluszahl-Paare in Frage
(Falls sich Zahlen in einem Tupel unterscheiden, können sie vertauscht werden):
\(1\) \(23-1=22\) \(22:2 =11\)
\((11,0); (10,1); (9,2); (8,3);\)
\((7,4); (6,5)\)
\(3\) \(23-3=21\) \(20:2=10\)
\((10,0); (9,1); (8,2); (7,3); \)
\((6,4); (5,5)\)
\(5\) \(23-5=18\) \(18:2=9\)
\((9,0); (8,1); (7,2); (6,3);\)
\((5,4)\)
\(7\) \(23-7=16\) \(16:2=8\)
\((8,0); (7,1); (6,2); (5,3); \)
\((4,4)\)
\(9\) \(23-9=14\) \(14:2=7\) \((7,0); (6,1); (5,2); (4,3)\)
\(11\) \(23-11=12\) \(12:2=6\) \((6,0); (5,1); (4,2); (3,3)\)
\(13\) \(23-13=10\) \(10:2=5\) \((5,0); (4,1); (3,2)\)
\(15\) \(23-15=8\) \(8:2=4\) \((4,0); (3,1); (2,2)\)
\(17\) \(23-17=6\) \(6:2=3\) \((3,0); (2,1)\)
\(19\) \(23-19=4\) \(4:2=2\) \((2,0); (1,1)\)
\(21\) \(23-21=2\) \(2:2=1\) \((1,0)\)
\(23\) \(23-23=0\) \(0:2=0\) \((0,0)\)
 
Tab. 2.2: Möglichkeiten von Pluszahl-Paaren in Abhängigkeit einer festen Startzahl und gleich bleibender Zielzahl 23
 
Der letzte Fall scheint trivial, um jedoch alle Möglichkeiten zu betrachten, darf er der Vollständigkeit wegen, nicht weggelassen werden.

Das Aufgabenformat Zahlengitter befasst sich aus dem Bereich Arithmetik vorrangig mit der Grundrechenart Addition und den Eigenschaften von Teilbarkeit und Primzahlen. Bezüglich der Addition kommen anhand der Aufgabe auch Kommutativgesetz, Assoziativgesetz und das Distributivgesetz zum Tragen (BEZOLD, 2010b). Dabei eröffnet die Aufgabe mit den unterschiedlichen Aufträgen ganz verschiedene Entdeckungen. Nachdem die Gestalt des Zahlengitters erfasst wurde, insbesondere ist hier die Entdeckung von Zusammenhängen zwischen den besonderen Feldern im Zahlengitter (Startzahl, Mittelzahl und Zielzahl) gemeint, sind unter Anwendung weiterer Fragen bisher unentdeckte Besonderheiten zu erkunden.
In der Literatur (vgl. SELTER, 2004; BEZOLD, 2012) wird dabei empfohlen anfangs Zahlengitter mit der Startzahl Null bearbeiten zu lassen und nachfolgend die gemachten Entdeckungen „auf Zahlengitter mit beliebiger Startzahl zu übertragen“ (BEZOLD, 2012, S. 82). Dieser Reihenfolge wird in der Aufgabe nicht nachgegangen, dennoch wird darauf verwiesen, den Fall der Startzahl 0 zu betrachten. Ob nun Zusammenhänge bei der Wahl 0 als Startzahl deutlich klarer erkennbar sind, scheint mir persönlich nicht ausreichend begründet. Durch die gewählte Aufgabenstellung ist der Hinweis zur Betrachtung der Startzahl 0 gegeben, sodass für Schülerinnen und Schüler verschiedene Zugangsmöglichkeiten eröffnet werden und dadurch möglichst für jeden Typ Entdecker die Zusammenhänge erkennbar werden sollten.
Das Format ermöglicht neben der näheren Untersuchung der Grundrechenart Addition aber auch Erkenntnisse, die in den Bereich Teilbarkeit und Primzahlen fallen. Teilbarkeitsuntersuchungen müssen bei diesem Aufgabenformat immer dann angestellt werden, wenn weitere Möglichkeiten von Pluszahl-Paar Kombinationen zu einem Gitter angegeben werden sollen, oder wenn nur die Zielzahl vorgegeben ist und daraus Startzahl und Pluszahl generiert werden sollen. Dies führt dann bspw. zu der Erkenntnis, dass bei der Wahl Null als Startzahl eine ungerade Zielzahl und damit insbesondere Primzahlen unmöglich sind.

Inhaltsbezogene Kompetenzformulierungen
 
Zahlen und Operationen 
Zahldarstellungen, Zahlbeziehungen, Zahlvorstellungen 
„Die Schülerinnen und Schüler vergleichen, strukturieren, zerlegen Zahlen und setzen sie zueinander in Beziehung“ (Kerncurriculum Niedersachen im Fach Mathematik für die Grundschule, S.19)
Diese Kompetenz wird sowohl am Ende des  Schuljahrgangs 2 als auch am Ende des Schuljahrgangs 4 erwartet. Bereits in Aufgabenteil b) ist ein Vergleich der verwendeten Pluszahlen notwendig, um eine Veränderung ausfindig machen zu können. In den Aufgabenteilen c) - f) ist ein Strukturieren und Zerlegen der Zahlen notwendig, um zu der jeweiligen Aufgabenstellung eine Lösung zu finden. Hat man bspw. aus b) geschlossen, dass sich das Zahlengitter nicht verändert, falls die Pluszahlen addiert die gleiche Summe wie zuvor bilden, so können in Teil c) durch Zerlegen des Ergebnisses, weitere Möglichkeiten gefunden werden. 
 
Operationen verstehen 
„Die Schülerinnen und Schüler verfügen über Grundbegriffe aus den Bereichen Addition, Subtraktion, Multiplikation und Division“ (ebd., S. 20) 
 Diese Kompetenz trifft in Bezug auf die gestellte Aufgabe nur auf die Rechenoperation Addition zu.
 
Operationen beherrschen 
„Die Schülerinnen und Schüler kennen die Zahlzerlegungen (bis 10) auswendig und nutzen sie in Aufgabenstellungen“ (ebd.) und „führen schriftliche Rechenverfahren sicher aus: Addition mit mehreren Summanden, […]“ (ebd., S. 21) 
Die zuerst genannte Kompetenz ist bei der Bearbeitung von Teilaufgabe c) von Vorteil. Zwar müssen dazu, bei den hier gewählten Pluszahlen, auch Zahlzerlegungen größer als 10 gefunden werden, dies schließt die formulierte Kompetenz jedoch nicht aus. Die zweit genannte Kompetenz findet bereits beim Ausfüllen des Zahlengitters Anwendung. Gerade das Einsetzen größerer Zahlen in das Zahlengitter kann Schülerinnen und Schüler dazu veranlassen, die geforderten Additionsaufgaben schriftlich auszuführen. 
 
 
 
Prozessbezogene Kompetenzformulierungen
 
Kommunizieren und Argumentieren 
„Die Schülerinnen und Schüler verwenden eingeführte mathematische Fachbegriffe sachgerecht“, „stellen Vermutungen über mathematische Sachverhalte an, begründen und überprüfen sie“ sowie „entdecken und beschreiben mathematische Zusammenhänge“ (Kerncurriculum Niedersachsen für die Grundschule im Fach Mathematik, S. 15) 
Die Kompetenz „beschreiben mathematische Sachverhalte mit eigenen Worten und finden dazu Fragestellungen“ (ebd.) wird nicht aufgeführt, da der zweite Satzteil auf die Aufgabe nicht zutrifft. Die Kompetenz „verwenden eingeführte mathematische Fachbegriffe sachgerecht“ tritt bspw. in Aufgabenteil e) hervor. Hier wird eine sachgerechte Verwendung des Fachbegriffs „Summe“ betont. Ebenso wird mit diesem Aufgabenteil die Kompetenz „entdecken und beschreiben mathematische Zusammenhänge“ (ebd.) angesprochen, denn die Schülerinnen und Schüler werden explizit dazu aufgefordert, Zusammenhänge zwischen Startzahl, Mittelzahl und Zielzahl zu entdecken und zu beschreiben. In Anlehnung an den beschriebenen Argumentationsprozess nach Bezold lassen sich weitere Kompetenzen formulieren, die sicherlich den bereits genannten Kompetenzen ähneln. Diese könnten z.B. wie folgt lauten: Die Schülerinnen und Schüler
  • stellen Vermutungen über mathematische Zusammenhänge an,
  • formulieren mathematische Entdeckungen in eigenen Worten,
  • hinterfragen die gefundenen Entdeckungen,
  • und versuchen diese zu begründen.

Die Nennung dieser Kompetenzen soll verdeutlichen, dass mit jeder gestellten Aufgabe, neben den vorformulierten Kompetenzen aus dem Kerncurriculum noch weitere davon abweichende Fertigkeiten und Fähigkeiten eingeübt werden können. Das Curriculum stellt lediglich eine Orientierungshilfe dar. In dem Teil zum Argumentieren wurde herausgestellt, dass vor allem den Bausteinen 2 und 3 des Argumentationsprozesses nach Bezold mit den aufgeführten Kompetenzen kaum gerecht geworden wird. Die Formulierung weiterer Kompetenzen soll aber aufzeigen, dass die ausgewählte Aufgabe jeden Baustein des Argumentierens anspricht.
 

Problemlösen 
„Die Schülerinnen und Schüler nutzen Zusammenhänge und übertragen sie auf ähnliche Sachverhalte“ (Kerncurriculum Niedersachen im Fach Mathematik für die Grundschule, S. 18)
Diese Kompetenz kommt in den Aufgaben c) - f) zum Tragen, denn das Wissen, welches in Aufgabenteil b) gewonnen wird, kann auf die anderen Teilaufgaben bezogen werden 
 
 
 
 
Die angeführten prozessbezogenen Kompetenzen finden sich überwiegend als Erwartungen am Ende des Schuljahrgangs 4 wieder, die inhaltsbezogenen Kompetenzen bereits am Ende des Schuljahrgangs 2. Da jedoch gerade die prozessbezogene Kompetenz des Argumentierens im Vordergrund steht, sollte die Aufgabe erst in der 3./4. Klassenstufe umgesetzt werden.

Heuristische Hilfsmittel: 
  • Das Zahlengitter ist eine Informative Figur. Es enthält alle wichtigen Informationen die zur Lösung der Aufgabe notwendig sind und alle Aufgabenstellungen a) bis f) sind auf dieses bezogen.
 
  • Beim zweiten Lösungsweg zur Aufgabe f) werden Tabellen benutzt, um mögliche Fälle und Zusammenhänge zu veranschaulichen.
 
 
Heuristische Strategien: 
  • Beim Ausfüllen des Zahlengitters in Aufgabenteil a) wird ausgehend von der gegebenen Startzahl vorwärts gearbeitet bis hin zur Zielzahl.
 
  • Aufgabenteil b) bis c) sowie f) wird durch Systematisches Probieren gelöst. Dabei handelt es sich um ein kombiniertes Vorwärts- und Rückwärtsarbeiten.
 
  • In Aufgabenteil c) wird von der Zielzahl ausgegangen und es werden mögliche Pluszahlen gesucht, wobei rückwärts gearbeitet wird.
 
 
Heuristische Prinzipien: 
  • Bereits in Aufgabenteil a) wird das Symmetrieprinzip genutzt. Die Schülerinnen und Schüler erkennen, dass in einer Zeile bzw. in jeder Spalte in jedem Schritt die gleiche Zahl addiert werden muss und somit immer gleich vorgegangen wird.
 
  • Bei Aufgabenteil b) wird untersucht, was sich ändert, wenn man die Pluszahlen ändert. Dabei werden verschiedene Veränderungen der Pluszahlen vorgenommen. Demnach wird dem Fallunterscheidungsprinzip nachgegangen.
 
  • In den Aufgabenteilen c) - f) ist ein Strukturieren und Zerlegen der Zahlen notwendig, um zu der jeweiligen Aufgabenstellung eine Lösung zu finden. Hat man bspw. aus b) geschlossen, dass sich das Zahlengitter nicht verändert, falls die Pluszahlen addiert die gleiche Summe wie zuvor bilden, so können in Teil c) durch Zerlegen des Ergebnisses, weitere Möglichkeiten gefunden werden. Somit ist das Zerlegungsprinzip bei der Lösung der Aufgabe von Bedeutung.
 
  • Bei Lösung von Aufgabe c) und  f) spielt außerdem das Invarianzprinzip eine Rolle, da die Zielzahl fest bleibt, und überlegt wird, wie sich die restlichen Elemente des Zahlengitters verändern können.

Die Aufgabe hat mit 1 Punkt (bzw. 2 Punkten) einen Schwierigkeitsgrad von *.
 
 
Sprachlogische Komplexität: 
Die Aufgabenstellungen des Zahlengitters sind jeweils in kurzen verständlichen Sätzen formuliert. Es treten weder logische Rückbezüge auf, noch werden logische Funktionen wie Negation etc. verwendet. Die Aufgabenstellung in Teil d) ist etwas anspruchsvoller und könnte als einzige der Stufe 1 zugeordnet werden, da mit der Frage „wie viele Möglichkeiten gibt es?“ implizit alle Möglichkeiten gefordert werden, was aus der Beschreibung der schwierigkeitsgenerierenden Merkmale eine besondere Herausforderung darstellt. Neben der bloßen Nennung aller Lösungen wird eine plausible Begründung verlangt, warum alle Lösungen gefunden wurden und es keine weiteren mehr gibt.
 
 
Kognitive Komplexität: 
In Aufgabenteil a) muss das Zahlengitter lediglich nach angegebenen Rechenschritten ausgefüllt werden, weshalb keine hohe „Kognitive Komplexität“ vorliegt und kann daher klar der Stufe 0 zugeordnet werden. Die anderen Aufgabenteile rufen die Schülerinnen und Schüler jedoch zu einer aktiven Auseinandersetzung mit dem Kontext Zahlengitter auf und fordern zum Teil die Organisation von mehreren Denkvorgängen (z.B. Aufgabenteil ‚e)‘), womit sie eindeutig der Stufe 1 zugeordnet werden können. Da für die Bearbeitung der weiterführenden Aufgabenteile keine heuristischen Strategien notwendig sind, ist die Abgrenzung zu Stufe 2 deutlich.
 
 
Formalisierung von Wissen: 
In Aufgabenteil a) wird in keinerlei Weise die „Formalisierung von Wissen“ verlangt. In den Aufgabenteilen b) - f) ist dies zwar durchaus der Fall, allerdings reichen wenige Präzisierungen aus, womit die Aufgabe insgesamt der Stufe 0 zuzuweisen ist. Präzisierungen sind hier bei der Formulierung der Zusammenhänge oder bei der Beschreibung von Veränderungen aufgrund einer Abänderung der Pluszahlen nötig. Eine Formalisierung wäre an diesen Stellen denkbar, wenn man die Pluszahlen als Platzhalter für beliebige natürliche Zahlen (und damit als Variable) ansieht. Daraus ließen sich die Zusammenhänge von Startzahl, Mittelzahl und Zielzahl ohne Betrachtung beispielhafter Pluszahlen ablesen. Dies wird jedoch nicht verlangt, es reicht ebenso diese Zusammenhänge durch Worte auszudrücken und zu begründen.
 
 
Formelhandhabung: 
Da bereits festgestellt wurde, dass das Merkmal „Formalisierung von Wissen“ der Stufe 0 zugeordnet werden kann, ist ein Umgang mit Formeln bei dieser Aufgabe nicht notwendig. Ebenso wurde beschrieben, dass allgemeine Abhängigkeiten der Startzahl, Mittelzahl und Zielzahl mithilfe der Verwendung von Variablen aufgestellt werden. Da dies jedoch für einen erfolgreichen Lösungsweg nicht zwingend notwendig ist, kann die Aufgabe auf Stufe 0 eingeordnet werden.
 
 
Stufenzuordnung: 
Formalisierung von Wissen
Stufe 0
Formelhandhabung
Stufe 0
Kognitive Komplexität
Stufe 0
Stufe 1
Sprachlogische Komplexität
Stufe 0
Stufe 1

Hilfestellungen: 
Um geeignete Hilfestellungen anzubieten, müssen zunächst Faktoren bei der Aufgabenbearbeitung ausfindig gemacht werden, die zu Schwierigkeiten führen könnten. Bereits in Teilaufgabe b) ist zu erwarten, dass zwar eine Veränderung festgestellt wird, jedoch die Verschriftlichung dessen, womit die Änderung zusammenhängt, den Schülerinnen und Schülern schwerfällt. Da die Erkenntnisse aus diesem Teil jedoch maßgeblich die gelingende Bearbeitung der weiteren Teilaufgaben bedingt, empfiehlt es sich, für diese Schwierigkeit Hilfestellungen zu formulieren. Anhand dessen sollte dann auch die Teilaufgabe c) gelingen. Bei Aufgabenteil d) sollten solche Hilfestellungen formuliert werden, die darauf hindeuten, dass verlangt wird, alle Möglichkeiten anzugeben. Während der Bearbeitung von Teil e) werden vermutlich ähnliche Probleme wie im Aufgabenteil b) auftreten. Werden die Zusammenhänge in b) nicht erkannt, so fehlen elementare Vorstellungen für die erfolgreiche Lösung von e). Die gewonnenen Erkenntnisse müssen dann schließlich in Teil f) selbst umgesetzt werden. Dabei muss beispielsweise bedacht werden, dass nur mit einer ungeraden Startzahl zu einer ungeraden Zielzahl gelangt werden kann. Es zeigt sich, dass an vielen Stellen der Durchführung Probleme auftreten können. Für die beschriebenen kritischen Stellen sollen nun Hilfestellungen angegeben werden:
 
Allgemein-strategische Hilfen Inhaltsorientierte strategische Hilfen Inhaltliche Hilfen
Lies dir die Aufgabe genau durch.
Wie kann die Summe von zwei beliebigen natürlichen Zahlen aussehen? (zwei gerade, zwei ungerade, gerade und ungerade)
Was ändert sich, wenn nur eine Pluszahl verändert wird? Wie sieht es aus, wenn beide gleichmäßig verändert werden? Und schließlich, wie verhält es sich, wenn eine Pluszahl vergrößert und die andere verkleinert wird?
Gibt es Angaben, die dir zur Bearbeitung fehlen?
Kennst du eine Möglichkeit, die gleiche Summe mit unterschiedlichen Summanden zu bilden?
Wie kannst du ohne Ausfüllen des oberen mittleren Feldes und des linken mittleren Feldes auf direktem Weg die Mittelzahl bestimmen?
Was kannst du aus den gegebenen Informationen ermitteln?
Überprüfe, ob dein Ergebnis und die Rechnungen korrekt sind.
Wie kannst du sichergehen, dass alle Lösungen gefunden wurden?
 
 
Sozialformen: 
Gruppenexploration (Einzelarbeit, Partnerarbeit und Gruppenarbeit möglich)
 
 
Differenzierungsmöglichkeiten: 
Für leistungsstärkere Schülerinnen und Schüler kann der Schwierigkeitsgrad der Aufgabe durch eine Erweiterung des Gitters, von einem 3x3 Gitter zu einem 4x4 Gitter, angepasst werden. Dabei kann dann wieder nach Zusammenhängen von Startzahl und Zielzahl gefragt werden, jedoch entfällt die Betrachtung der Mittelzahl, weil das Gitter eine gerade Anzahl an äußeren Feldern aufweist. Die Betrachtung eines 4x4 Gitters mit der Startzahl 0 führt so bspw. zu der Entdeckung, dass die Zielzahlen immer Vielfache von 3 sind (STEINBORN, 2005, S. 12).
 
Beispiel: Erweiterung zu einem 4x4 Gitter:
                                          Abb. 1: 4x4 Zahlengitter
 

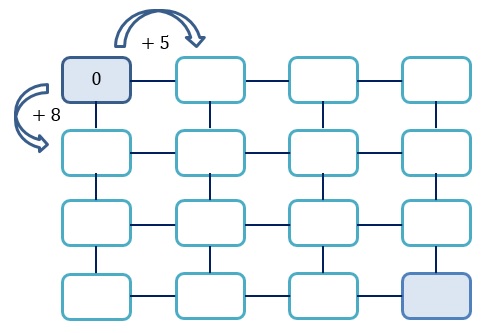
Denkbar wäre auch eine Betrachtung eines nicht-quadratischen Gitters. Neben der Veränderung der Größe eines Zahlengitters, kann aber auch anhand der verwendeten Zahlen und Operationen differenziert werden. Eine Umpositionierung der gegebenen Zahlen innerhalb des Zahlengitters impliziert so auch eine Veränderung des Aufgabentyps. Teilaufgabe a) stellt eine klassische „Bestimmungsaufgabe“ (BRUDER, 2005) dar. Als „Umkehraufgabe“ (ebd.) würden dann die Zielzahl und das Pluszahl-Paar vorgegebenen werden. Es kann aber auch eine der beiden Diagonalen des Zahlengitters angegeben werden. Weitere ähnliche Variationen und Problemstellungen sind bei SELTER (2004, S. 44) zu finden. Statt der ausschließlichen Verwendung der Grundrechenart Addition, kann auch die Multiplikation oder Subtraktion aufgenommen werden. Bei Veränderung der Pluszahlen zu Minuszahlen muss jedoch darauf geachtet werden, dass die verwendeten Zahlen Ergebnisse größer gleich Null liefern. Ist der Zahlenraum bereits von natürlichen Zahlen zu negativen Zahlen erweitert und sind die dazugehörigen Grundvorstellungen erfolgreich vermittelt worden, so kann natürlich ohne weitere Überlegungen mit Minuszahlen gearbeitet werden.
 
Für leistungsschwächere Schülerinnen und Schüler kann analog das Gitter weiter verkleinert werden oder unterstützende Elemente hinzugefügt werden. So ein Element könnte hier derart aussehen, dass zusätzlich zu dem Pfeil noch Platz für eine schriftliche Rechnung geschaffen wird. Zur Bewältigung der weiterführenden Aufgabe kann neben dem Einsatz der aufgeführten Lernhilfen, vor allem bei Teilaufgabe e), eine Unterstützung dadurch stattfinden, dass Worte wie „doppelt“, „Summe“, „Pluszahl“ vorgegeben werden und in der Erklärung der Zusammenhänge Anwendung finden sollen.

Die Aufgabe kann in einer Gruppenexploration umgesetzt werden. Bei einer Gruppenexploration geht es um „die Entdeckung mathematischer Zusammenhänge“ (BARZEL, BÜCHTER, & LEUDERS, 2011, S. 90), welche durch die Betrachtung vieler verschiedener Beispiele ermöglicht wird. Die Untersuchung der Beispiele wird dabei aufgeteilt. In Bezug auf die Aufgabe kann bspw. eine Gruppe mehrere Zahlengitter mit der Startzahl Null und eine weitere Zahlengitter mit anderer Startzahl betrachten. Gleichermaßen ist denkbar, dass die zu erkennenden Veränderungen bei Abwandeln der Pluszahlen arbeitsteilig untersucht werden. Die Lehrperson präsentiert also zunächst die Aufgabe der Klasse. Dann werden in einem zweiten Schritt die Beispiele aufgeteilt und daran anschließend untersucht. Die Aufteilung und Untersuchung kann dabei sowohl in Einzel-, Partner- als auch Gruppenarbeit stattfinden. Abschließend werden die Entdeckungen in der Gruppe bzw. der Klasse zusammengetragen und besprochen. Mit der Methodenauswahl der Gruppenexploration können die Schülerinnen und Schüler erleben, dass mit dem kooperativen Arbeiten eine Untersuchung vieler, ganz unterschiedlicher Beispiele möglich ist, die in Einzelarbeit gar nicht denkbar gewesen wären. Zudem ist so das Arbeiten von Gruppen auf unterschiedlichem Niveau gegeben. Einige Gruppen werden beispielsweise eifrig weitere Zahlengitter untersuchen, andere hingegen werden nur die in der Aufgabe angegebenen Zahlengitter betrachten. Treffen die Schülerinnen und Schüler diese Einteilung der Arbeit nach Anforderungsniveau selbst, so „werden sie […] zu Akteuren der Binnendifferenzierung“ (BARZEL ET. AL., S. 90).


Bearbeitet von: Lara Pertz (hochgeladen von Marisa Pfläging)
nach oben
502 Nutzer/-innen haben abgestimmt.

Feedback

Wir freuen uns auf Ihre Anregungen und konstruktive Rückmeldung zum Material.