Flächenberechnung von zusammengesetzten Figuren
| Klasse | Schulstufe | Thema | Themengebiet | Schwierigkeit |
|---|---|---|---|---|
| 6 | Sekundarstufe I | Flächeninhalt | Raum und Form | ** |
| Heuristsche Hilfsmittel | Heuristische Prinzipien | Heuristische Strategien |
|---|---|---|
| Informative Figur | Zerlegungs- und Ergänzungsprinzip, Symmetrieprinzip | Vorwärtsarbeiten, Systematisches Probieren |
Aufgabenstellung

Quellenangabe:
- Lösung
- Themengebiet
- Geförderte Kompetenzen
- Heurismen
- Schwierigkeitsgrad
- Umsetzung im Mathematikunterricht
- Einsatzmöglichkeiten


Der Flächeninhalt des gelben Rechtecks beträgt: \(8cm\cdot (6cm-(2cm+2cm))={ 16cm }^{ 2 }\)
Der Flächeninhalt des roten Rechtecks beträgt: \(10cm⋅2cm=20cm^{ 2 }\)
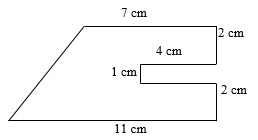
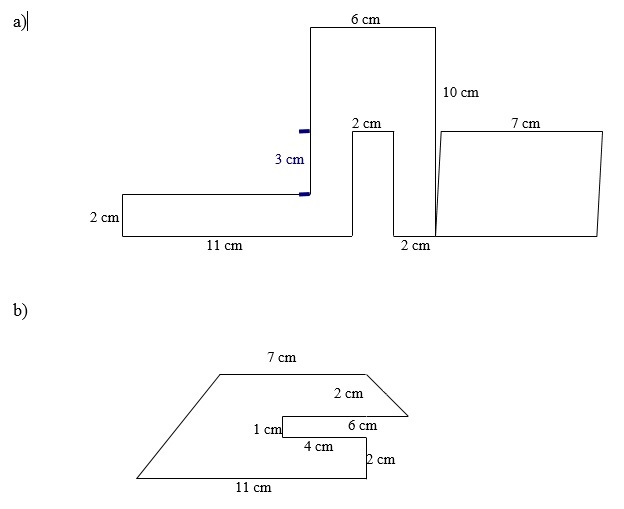
Um den Flächeninhalt der Figur bestimmen zu können, teilen wir diese in drei Rechtecke auf und ergänzen das entstandene Dreieck durch ein kongruentes Dreieck zu einem Rechteck.
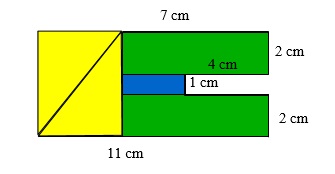
Wir wissen, dass die beiden grünen Rechtecke gleich groß sind, da die kürzere Seite jeweils \(2 cm\) und die längere Seite jeweils \(7 cm\) misst, und wegen der Symmetrie. Also können wir den Flächeninhalt der grünen Rechtecke mit der Flächeninhaltsformel für Rechtecke berechnen: \(2cm⋅7cm=14cm^2\)
Wir wissen bereits, dass die kurze Seite des blauen Rechtecks \(1 cm\) lang ist. Um die längere Seite zu bestimmen, rechnen wir: \(7cm – 4cm = 3cm\). Nun können wir wieder die Flächeninhaltsformel anwenden: \(1cm⋅3cm=3cm^2\)
Nun berechnen wir den Flächeninhalt des gelben Rechtecks: \(4cm⋅5cm=20cm^2\)
Allerdings ist ursprünglich nur das eine gelbe Dreieck gegeben, welches genau die Hälfte des entstandenen gelben Rechtecks ausmacht. Deshalb müssen wir nur die Hälfte des Flächeninhaltes des gelben Rechtecks berücksichtigen, also \(20cm^2:2=10cm^2\)
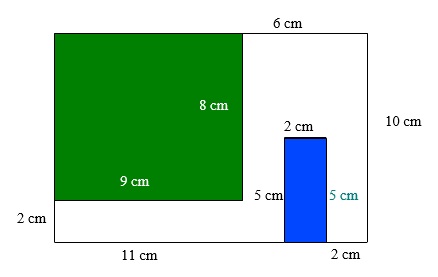
Der Flächeninhalt des entstandenen Rechtecks beträgt: \(10cm⋅(11cm+2cm+2cm)=150cm^2\)
Der Flächeninhalt des grünen Rechtecks beträgt: \(8cm⋅9cm=72cm^2\)
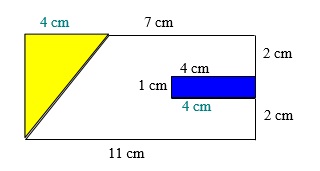
Um den Flächeninhalt des gelben Dreiecks zu berechnen, gehen wir folgendermaßen vor:
Wir zerlegen nun wieder die Figur ähnlich wie bereits in 3a), sodass aus dem Dreieck wieder ein Rechteck entsteht.

Schülerinnen und Schüler sollen die Kompetenz erlangen, Flächeninhalte von Rechtecken und Quadraten zu bestimmen (KC: Größen und Messen 3.6.2). Dies sollen sie auch bei zusammengesetzten Figuren bestimmen, indem sie die Figur in Rechtecke bzw. Quadrate unterteilen (KC: Größen und Messen 3.6.3). Diese Kompetenz, den Flächeninhalt und Umfang von zusammengesetzten Figuren zu bestimmen, wird in unserer ausgewählten Aufgabe trainiert. Dafür müssen sie verwendete Größen (in unserem Beispiel: Längen und Flächeninhalt) unterscheiden, was einer weiteren Kompetenz im Kerncurriculum (Größen und Messen: 1.6.2) entspricht.
Das Berechnen von Flächeninhalten ist ein wichtiges Thema, weil es die Grundlage für Volumenberechnungen ist.
Wir haben uns dafür entschieden, diese Aufgabe in einer sechsten Klasse zu behandeln. Die Flächeninhaltsberechnung vom Rechteck und Quadrat sollte bereits als Thema behandelt worden sein. An dieses Thema könnte man mit dieser Aufgabe gut anschließen, um zur Flächeninhaltsberechnung zusammengesetzter Figuren überzuleiten, welche laut dem Kerncurriculum auch eine Kompetenz ist, die am Ende des sechsten Jahrgangs beherrscht werden sollte.
Unsere Teilaufgabe a) sieht ausschließlich die Zerlegung in Rechtecke vor, bzw. die Ergänzung mit Hilfe von Rechtecken zu einem großen Rechteck. Die Teilaufgabe b) gestaltet sich hier schon als etwas schwieriger, denn in dieser Figur ist ein Dreieck vorhanden, welches durch ein weiteres Dreieck zu einem Rechteck ergänzt werden kann. Dadurch sollen die Schülerinnen und Schüler herausfinden, dass der Flächeninhalt des entstandenen Rechtecks genau doppelt so groß ist wie der gesuchte Flächeninhalt des Dreiecks. Da die Flächeninhaltsberechnung von Dreiecken erst im siebten oder achten Schuljahr thematisiert wird, ist dies schon eine Vorbereitung dafür. Das ist ein weiterer Grund diese Aufgabe nicht bereits im fünften, sondern erst Mitte des sechsten Schuljahres zu behandeln.
"Die Schülerinnen und Schüler berechnen Flächeninhalt [...] von Quadrat und Rechteck.", "Die Schülerinnen und Schüler berechnen Flächeninhalt [...] zusammengesetzter Figuren." (KC, Ende Schuljahrgang 6, S.27)
"Die Schülerinnen und Schüler erkennen und benennen Eigenschaften von Rechteck, Quadrat, Dreieck und Kreis." (KC, Ende Schuljahrgang 6, S.28)
"Die Schülerinnnen und Schüler wenden die Strategie des Zerlegens und Zusammensetzens an." (KC, Ende Schuljahrgang 6, S.19)
"Die Schülerinnen und Schüler lösen Probleme durch Probieren." (ebd.)
"Die Schülerinnen und Schüler nutzen Darstellungsformen wie Tabellen, Skizzen oder Graphen zur Problemlösung." (ebd.)
- Als heuristisches Hilfsmittel wird eine Skizze genutzt, welche eine Informative Figur ist. Die möglichen Zerlegungen und Ergänzungen werden in den Figuren skizziert, sodass einzelne Figuren erkannt werden können und so der Flächeninhalt dieser berechnet werden kann.
- Es wird systematisch ausprobiert, wie die Figuren am Besten zerlegt werden können, damit möglichst viele Seitenlängen bereits gegeben sind und diese nicht berechnet werden müssen.
- In Bezug auf das „Vorwärstarbeiten“ wird bei der ersten Lösungsmöglichkeit die gegebene Figur in mehrere Einzelfiguren zerlegt, dessen Flächeninhalt berechnet werden kann. Anschließend werden die Flächeninhalte summiert und der gesuchte Flächeninhalt wird erhalten. Bei der zweiten Lösungsmöglichkeit wird eine Figur so ergänzt, dass ein Rechteck entsteht. Es wird der kompletten Flächeninhalt berechnet und das subtrahiert, was zu viel berechnet wurde.
- Wie bereits beim „Vorwärtsarbeiten“ erwähnt wurde, wurde sowohl das Prinzip des Ergänzens als auch das des Zerlegens angewandt. Bei Teilaufgabe b) haben wir die Figur so zerlegt, dass an der linken Seite ein Dreieck entsteht, welches wir durch Ergänzung eines gleich großen Dreieck wieder zu einem Rechteck konstruieren konnten. Bei der Ergänzung ist zu beachten, dass die Flächen, die zu viel berechnet wurden, im Nachhinein wieder abgezogen werden.
- Mithilfe des Symmetrieprinzips werden die fehlenden Seitenlängen bestimmt, denn die Symmetrien der einzelnen Rechtecke sind bekannt.
| Allgemein-strategische Hilfen | Inhaltsorientierte strategische Hilfen | Inhaltliche Hilfen |
|
Kennst du eine ähnliche Aufgabe?
|
Wie lautet die Formel?
|
Hast du einzelne Flächen mehrmals berechnet?
|
|
Was hast du gegeben? |
Von welchen geometrischen Figuren kannst du den Flächeninhalt berechnen?
|
Berechne zunächst die einzelnen Flächeninhalte und addiere diese anschließend.
|
|
Was fehlt dir noch?
|
Kannst du die Figur zerlegen oder ergänzen?
|
Zerlege die Figur in Rechtecke.
|
| Allgemein-strategische Hilfen | Inhaltsorientierte strategische Hilfen | Inhaltliche Hilfen |
|
Kennst du eine ähnliche Aufgabe?
|
Kannst du hier besser ergänzen oder zerlegen?
|
Kannst du aus dem Dreieck durch Ergänzung ein Rechteck machen?
|
|
Sieh dir die Figur noch einmal genau an.
|
Kannst du etwas ergänzen, um es dir zu erleichtern?
|
Wie genau kommst du vom Flächeninhalt des Rechtecks auf den Flächeninhalt des Dreiecks?
|
|
Entwirf einen Plan.
|
Sind dir alle Seitenlängen bekannt, die du benötigst?
|
Wie oft passt das Dreieck in das neue Rechteck?
|
- Einzelarbeit
- Partnerarbeit
Die Figuren sehen dann folgendermaßen aus:
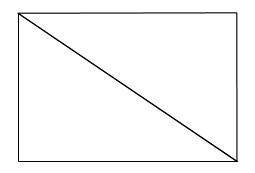
Damit sollte ihnen deutlich werden, dass ein Rechteck in zwei gleich große Dreiecke unterteilt werden kann. Somit kann das Dreieck zu einem Rechteck ergänzt werden. Der Flächeninhalt ist dann halb so groß, wie der des zugehörigen Rechtecks.
Bearbeitet von: Lina Cappel, Marina Kröger (hochgeladen von Marisa Pfläging)
Feedback
Wir freuen uns auf Ihre Anregungen und konstruktive Rückmeldung zum Material.
Copyright © 2014-2017 - Ana Kuzle
