Zaunaufgabe
| Klasse | Schulstufe | Thema | Themengebiet | Schwierigkeit |
|---|---|---|---|---|
| 5 | Primarstufe | Umfang von Rechtecken | Größen und Messen, Raum und Form, Zahlen und Operationen | **, *** |
| Heuristsche Hilfsmittel | Heuristische Prinzipien | Heuristische Strategien |
|---|---|---|
| Informative Figur, Tabelle, Gleichungen | Invarianzprinzip, Extremalprinzip | Vorwärtsarbeiten, Kombiniertes Vorwärts- und Rückwärtsarbeiten, Systematisches Probieren, Analogieschlüsse |
Aufgabenstellung
Emilys Tante ist umgezogen. Vorher hatte sie zwei Gemüsebeete (siehe Bild). Im neuen Garten möchte sie nur noch ein großes, rechteckiges Beet anlegen. Emily soll die Zäune der alten Beete verwenden um das neue Beet zu umzäunen.
a) Welche Maße kann das neue Beet haben, damit die Zäune der alten Beete genau passen?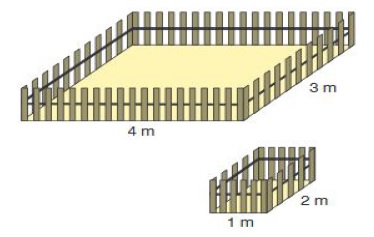
b) Gibt es noch weitere Lösungen? Welche?

b) Gibt es noch weitere Lösungen? Welche?
c) Bei welchen Maßen hat das Beet die größte Fläche?
Dokumentiere deinen Lösungsweg in nachvollziehbarer Weise.
Quellenangabe:
Original aus Gebel, I., & Kuzle, A. (2016). MatheWelt. Heft 196. Das Schülerarbeitsheft. mathematik lehren. S.10
- Lösung
- Themengebiet
- Geförderte Kompetenzen
- Heurismen
- Schwierigkeitsgrad
- Umsetzung im Mathematikunterricht
- Einsatzmöglichkeiten
Lösungsvariante 1 - Rechnerische Lösung
a)
alte Beete:
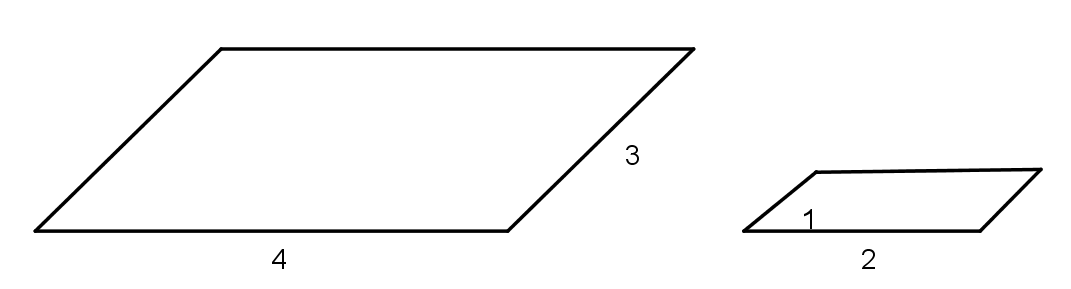
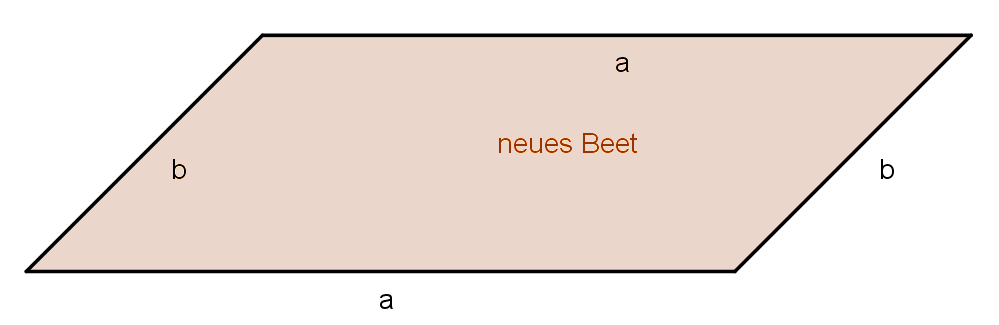
Zunächst wird der Umpfang des neuen Beetes berechnet, der sich aus den Seitenlängen der beiden alten Beete zusammensetzt:
\(U=2 \dot\ 4+2 \dot\ 3+2 \dot\ 2+2 \dot\ 1=8+6+4+2=20[m]\)
Die Zaunlänge von 20m muss nun so aufgeteilt werden, dass jeweils zwei Seiten gleich lang sind. Für den Umfang des neuen Beets gilt:
\(U=2 \dot\ a+2 \dot\ b\)
Die Umfangsformel kann wie folgt umgeformt werden:
| \(U=2 \dot\ 4+2 \dot\ 3+2 \dot\ 2+2 \dot\ 1\) | |
| \(\Leftrightarrow \) | \(U=2 \dot\ (4+2)+2 \dot\ (3+1)\) |
| \(\Leftrightarrow \) | \(U=2 \dot\ 6+2 \dot\ 4\) |
Somit ergibt sich \(a=6[m]\) und \(b=4[m]\).
Das neue Beet kann also die Maße 6m x 4m haben.
b)
Für den Umfang des neuen Beets gilt:
| \(U=a+a+b+b=2a+ 2 b\) | |
| \(\Rightarrow \) | \(20=2a+2b\) |\(-2a\) |
| \(\Leftrightarrow \) | \(2b=20-2a\) |\(:2\) |
| \(\Leftrightarrow \) | \(b=10-a\) |
Somit ergeben sich für die Seitenlängen a und b des neuen Beets mit einem Umfang von 20 m folgende Möglichkeiten:
| Seite a (in m) | Seite b (in m) |
| 1 | 9 |
| 2 | 8 |
| 3 | 7 |
| 4 | 6 |
| 5 | 5 |
| 6 | 4 |
| 7 | 3 |
| 8 | 2 |
| 9 | 1 |
Die blau markierten Maße wiederholen sich.
Somit gibt es noch vier weitere Möglichkeiten, also insgesamt fünf Möglichkeiten, für die Maße des neuen Beetes.
c)
Um zu ermitteln mit welchen Maßen das neue Beet die größte Fläche hat, wird die Flächeninhaltsformel für Rechtecke verwendet:
\(A=a \dot\ b\)
Es werden alle möglichen Flächen berechnet.
| Seite a (in m) | Seite b (in m) | Flächeninhalt A (in m²) |
| 1 | 9 | 9 |
| 2 | 8 | 16 |
| 3 | 7 | 21 |
| 4 | 6 | 24 |
| 5 | 5 | 25 |
Das Beet hat mit den Maßen 5m x 5m mit 25m² die größtmögliche Fläche.
Lösungsvariante 2 - Eine weitere rechnerische Lösung für die Aufgabenteile a) und b)
Gesucht ist der Umfang des neuen Beets.
Da das neue Beet die Form eines Rechtecks hat, reicht es aus zwei Seiten zu berechnen. Die beiden Seiten müssen zusammen 4+3+2+1 Meter, also 10 Meter lang sein.
neues Beet mit \(a+b=10\):
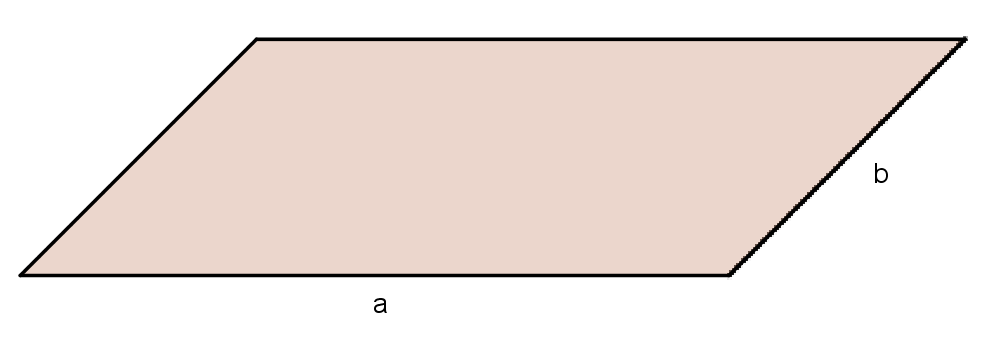
Durch Ausprobieren erhalten wir die folgenden Möglichkeiten für a und b:
| Versuch | Seite a | Seite b | a+b |
Kommentar:
Ich habe gerechnet...
|
| 1 | 1 | 9 | 10 | 1 plus wieviel ergibt 10? |
| 2 | 2 | 8 | 10 | 2 plus wieviel ergibt 10? |
| 3 | 3 | 7 | 10 | 3 plus wieviel ergibt 10? |
| 4 | 4 | 6 | 10 | 4 plus wieviel ergibt 10? |
| 5 | 5 | 5 | 10 | 5 plus wieviel ergibt 10? |
| 6 | 6 | 4 | 10 |
6 plus wieviel ergibt 10?;
Diese Kombination gab es schon.
|
Aufgabenteil a) und b) wurden somit gelöst. Ein mögliches Beet hat die Seitenlängen 1m und 9m und insgesamt gibt es fünf Lösungen.
Lösungsvariante 3 - Eine weitere rechnerische Lösung für den Aufgabenteil a)
Gegeben sind zwei Rechtecke \(R_1\) und \(R_2\). \(R_1\) hat die Seitenlängen \(a_1=4[m]\) und \(b_1=3[m]\). \(R_2\) hat die Seitenlängen \(a_2=1[m]\) und \(b_2=2[m]\).
Gesucht ist ein neues Rechteck der Seitenlängen \(a_3\) und \(b_3\).
Zunächst wird der Umfang der beiden Rechtecke \(R_1\) und \(R_2\) ermittelt.
| \(U_{ { R }_{ 1 } }=2\left( { a }_{ 1 }+{ b }_{ 1 } \right) \) | ; | \(U_{ { R }_{ 2 } }=2\left( { a }_{ 2 }+{ b }_{ 2 } \right) \) | |
| \(\Rightarrow \) | \(U_{ { R }_{ 1 } }=2( 4+3) \) | ; | \(U_{ { R }_{ 1 } }=2( 1+2) \) |
| \(\Leftrightarrow \) | \(U_{ { R }_{ 1 } }=14 [m]\) | ; | \(U_{ { R }_{ 1 } }=6[m]\) |
Durch Addition dieser erhält man den Umfang des neues Beets:
| \(U_{ { R }_{ 3 } }={ U }_{ { R }_{ 1 } }+{ U }_{ { R }_{ 2 } }\) | |
| \(\Rightarrow \) | \(U_{ { R }_{ 3 } }=14+6\) |
| \(\Leftrightarrow \) | \(U_{ { R }_{ 3 } }=20[m]\) |
Die Zaunlänge von 20m muss nun so aufgeteilt werden, dass jeweils zwei Seiten gleich lang sind.
| \(U_{ { R }_{ 3 } }=2\left( { a }_{ 3 }+{ b }_{ 3 } \right) \) | |
| \(\Rightarrow \) | \(20=2\left( { a }_{ 3 }+{ b }_{ 3 } \right) \) |\(:2\) |
| \(\Leftrightarrow \) | \(10 = a_3+b_3\) |
Da die beiden Variablen \(a_1\) und \(b_1\) unbekannt sind, nehmen wir \(a_3=7[m]\) an. Damit folgt:
| \(10=7+{ b }_{ 3 } \ \) |\(-7\) | |
| \(\Leftrightarrow \) | \(b_3=3[m]\) |
Das neue Beet hat also die Maße 7m und 3m.
Lösungsvariante 4 - Zeichnerische Lösung
Gegeben: zwei Rechtecke
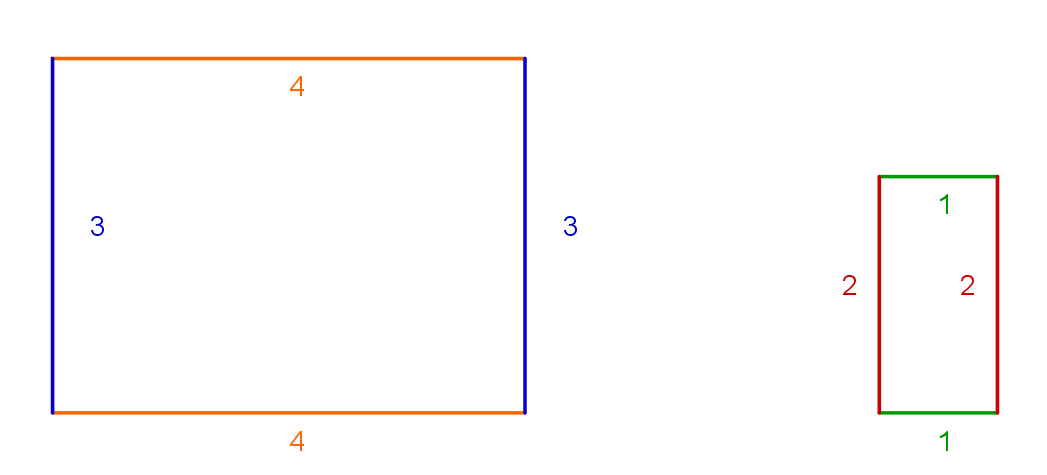
a)
Zerlegt man das zweite Rechteck in die einzelnen Seitenlängen und setzt diese an das erste Rechteck, so entsteht ein neues Rechteck:
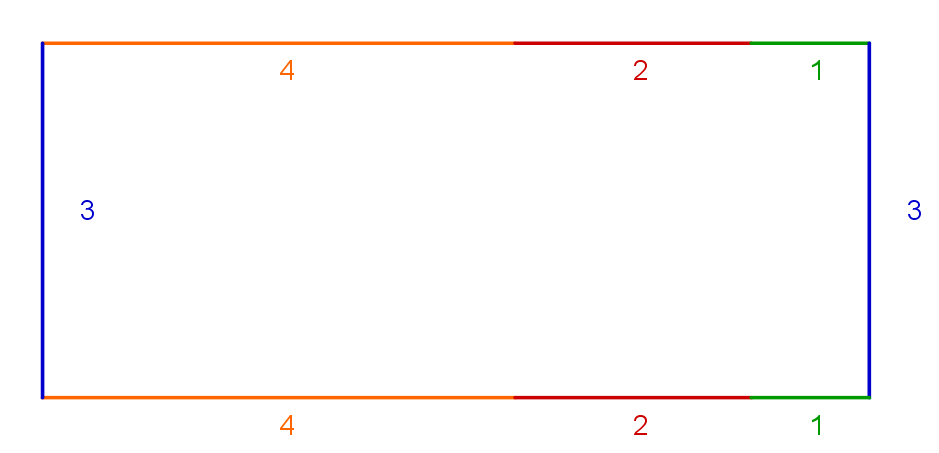
Das neue Beet kann 4+2+1=7 Meter lang und 3 Meter breit sein.
b)
Auf gleiche Weise wie in Aufgabenteil a) können die weiteren Möglichkeiten ermittelt werden:
|
Möglichkeit 2:
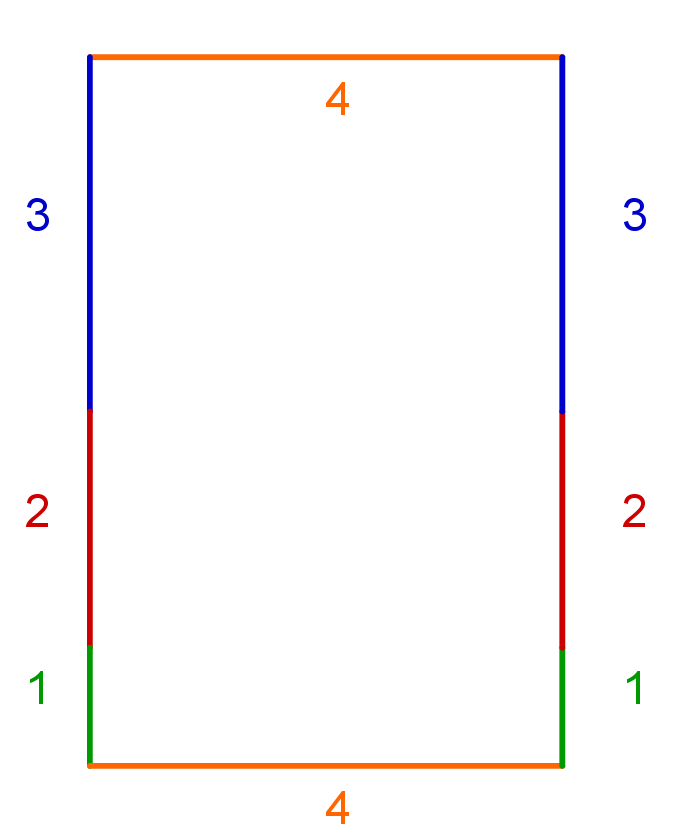 |
Möglichkeit 3:
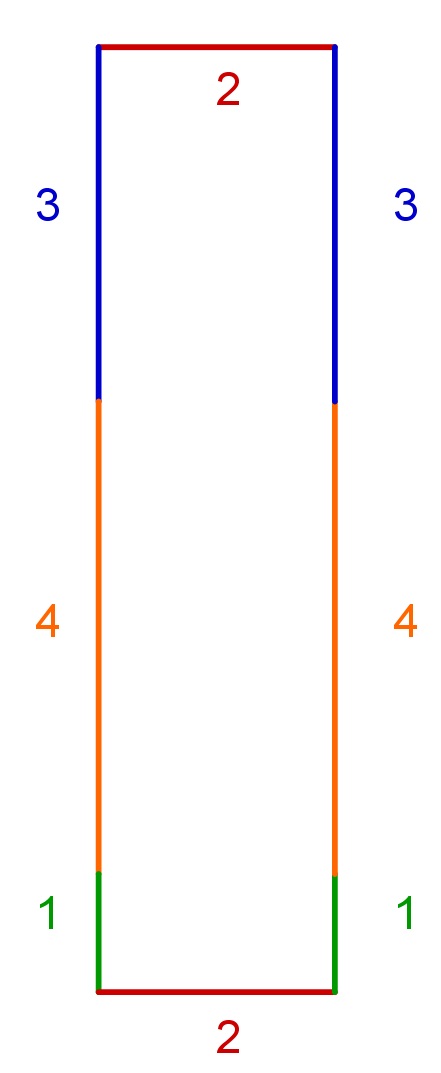 |
Möglichkeit 4:
 |
|
Möglichkeit 5:
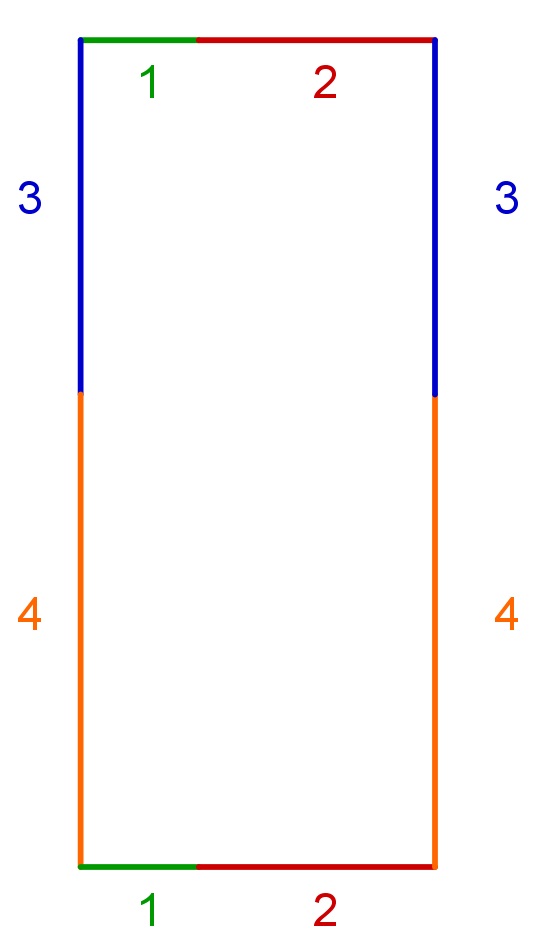 |
Möglichkeit 6:
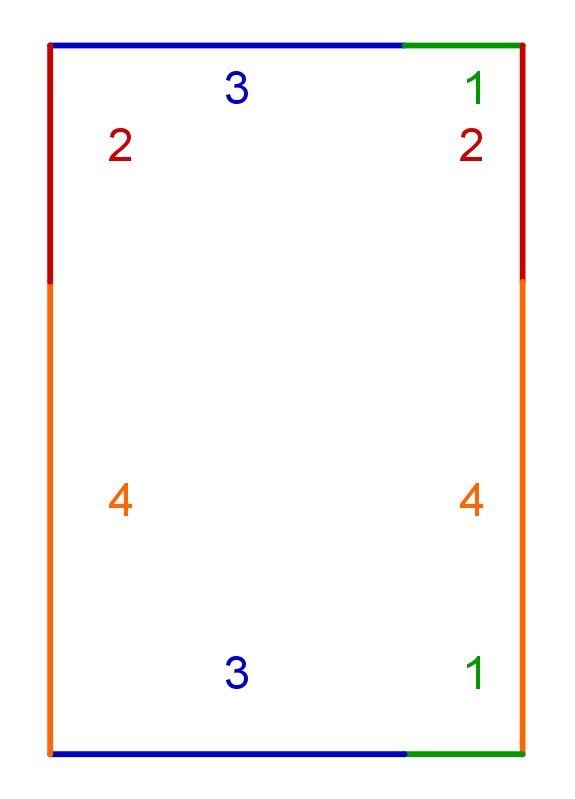 |
Möglichkeit 7:
 |
Es ist zu erkennen, dass Möglichkeit 2 und 6 das gleiche Rechteck mit den Maßen 4 m x 6 m ergeben. Außerdem ergibt die Variante aus Teilaufgabe a) und Möglichkeit 5 das gleiche Rechteck mit den Seitenlängen 3 m und 7m.
Somit gibt es insgesamt fünf Möglichkeiten das neue Beet einzuzäunen.
c)
Mit der Flächeninhaltsformel \(A= a \dot\ b\) für Rechtecke mit der Seitenlänge a und b ergibt sich für die Flächen der mäglichen Figuren aus Aufgabenteil b):
| \(A_2=4 \dot\ (3+2+1)=4 \dot\ 6=24[m²]\) |
| \(A_3=2 \dot\ (3+4+1)=2 \dot\ 8=16[m²]\) |
| \(A_4=1 \dot\ (3+4+2)=1 \dot\ 9=9[m²]\) |
| \(A_5=(1+2) \dot\ (4+3)=3 \dot\ 7=21[m²]\) |
| \(A_7=(4+1) \dot\ (3+2)=5 \dot\ 5=25[m²]\) |
Antwort: Bei der siebten Figur mit den Maßen 5m x 5m erhält man den größten Flächeninhalt.
Lösungsvariante 5 - Eine weitere zeichnerische Alternative für Aufgabenteil a)
Wir haben zwei Rechtecke gegeben, das eine hat Seitenlängen von 4m und 3m. Dieses zeichnen wir zunächst. Das andere Rechteck hat Seitenlängen von 1m und 2m. An dem ersten Rechteck werden jeweils einmal 1m und einmal 2m ergänzt (blaue Linien). Nun wird das neue Rechteck vervollständig (grüne Linien). Das neue Beet ist konstruiert. Es können die Maße durch die maßstabsgerechte Konstruktion abgemessen werden.
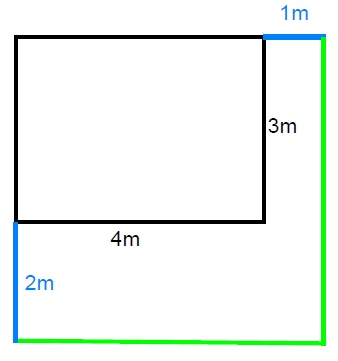
Antwort: Das neue Beet hat die Maße 5m und 5m.
Die Zaunaufgabe kann ab der fünften Klasse eingesetzt werden. Die im entsprechenden Abschnitt beschriebenen Kompetenzen lassen sich zwar den Niveaustufen B und C zuordnen und somit sollten Schülerinnen und Schüler der vierten Jahrgangsstufe in der Lage sein, die Aufgaben zu lösen (vgl. Rahmenlehrplan Teil C. Mathematik. Jahrgangstufen 1- 10.2015, S. 16), in MatheWelt 196 wird jedoch eine Verwendung für die fünfte Jahrgangsstufe empfohlen (vgl. Gebel und Kuzle 2016, S. 10). Der Grund hierfür liegt wahrscheinlich darin, dass die Berechnung des Umfanges von Rechtecken bereits fortgeschritten verstanden werden muss. Außerdem müssen die Schülerinnen und Schüler auch in der Lage sein, mithilfe der Formel zur Berechnung des Umfanges aus einem Umfang gesuchte Seitenlängen zu ermitteln. Dies ist schwieriger, da die Formel nicht direkt angewandt werden kann. Abschließend lässt sich daher sagen, dass nahezu alle Kinder der fünften Jahrgangstufe dazu in der Lage sein sollten, die Aufgabe zu lösen. Es ist zu vermuten, dass einige Kinder der vierten Klasse die Aufgabe ebenfalls lösen können.
Zu den mit dieser Aufgabe geförderten Kompetenzen zählen Kompetenzen aus dem prozessbezogenen Kompetenzbereich „Probleme mathematisch lösen“ sowie aus den inhaltsbezogenen Kompetenzbereichen „Größen und Messen“, „Raum und Form“ und „Gleichungen und Funktionen“ (vgl. Rahmenlehrplan Brandenburg "Teil C. Mathematik. Jahrgangsstufen 1-10. 2015", der ab dem Schuljahr 2017/18 gültig ist (im Folgenden als RLP bezeichnet)).
Inhaltsbezogene Kompetenzformulierungen
Größen und Messen:
Bei den inhaltsbezogenen Kompetenzbereichen wird der Bereich „Größen und Messen“ gefördert, indem die Schülerinnen und Schüler Größen in Sachzusammenhängen berechnen. So erwerben sie folgendermaßen als erste Kompetenz:
Die Schülerinnen und Schüler können mit Größenangaben rechnen. (vgl. RLP, Größen und Messen, Niveaustufe C, S.24)
Dabei müssen die Seiten des neuen Gartenbeets ermittelt werden, indem sowohl die Größe Umfang verwendet wird (Aufgabenteil a) und b)) als auch der größtmögliche Flächeninhalt berechnet wird (Aufgabenteil c)).
Raum und Form:
Der Kompetenzbereich „Raum und Form“ wird gefördert, indem die Schülerinnen und Schüler geometrische Objekte darstellen. Als zweite Kompetenz lässt sich formulieren:
Die Schülerinnen und Schüler können ausgewählte geometrische Objekte zeichnen. (vgl. RLP, Raum und Form, Niveaustufe B, S.26)
So ist es hilfreich, sich als Einstieg in die Aufgabe die Skizze der Aufgabenstellung in Form eines Rechtecks oder eines Parallelogramms abzuzeichnen und gegebenenfalls eine oder mehrere weitere Skizze(n) mit dem neu zu erstellenden Gartenbeet aufzuzeichnen (Aufgabenteile a) und b)).
Gleichungen und Funktionen:
Und schließlich wird auch der Kompetenzbereich „Gleichungen und Funktionen“ gefördert, indem die Schülerinnen und Schüler die Lösung mittels einer Gleichung bzw. eines Terms errechnen können (in allen Aufgabenteilen möglich). Daraus ergibt sich als dritte Kompetenz:
Die Schülerinnen und Schüler können Terme und Gleichungen darstellen. (vgl. RLP, Gleichungen und Funktionen, Niveaustufe C, S.28)
So lässt sich beispielsweise aus der Formel für den Umfang eine Gleichung erstellen, mithilfe derer eine Seitenlänge in Abhängigkeit zur anderen Seitenlänge ermittelt werden kann (Aufgabenteil b)) oder es lassen sich die Flächeninhalte mit Termen errechnen (Aufgabenteil c)).
Prozessbezogene Kompetenzformulierungen
Probleme mathematisch lösen
Der prozessbezogene Kompetenzbereich „Probleme mathematisch lösen“ wird insofern gefördert, dass die Schülerinnen und Schüler eine Aufgabe bearbeiten, welche sie vor ein bisher noch nicht bearbeitetes Problem stellt, so dass sie diese nicht mit bisher erworbenen Strategien lösen können (Aufgabenteil a)). Die erste Kompetenz lautet also:
Die Schülerinnen und Schüler können Aufgaben bearbeiten, zu denen sie noch keine Routinestrategie haben. (vgl. RLP, S.19)
Um der Lösung auf die Spur zu kommen, geht damit die zweite zu erwerbende Kompetenz einher:
Die Schülerinnen und Schüler können eine Lösungsstrategie entwickeln, die vom zufälligen Probieren (wie in Aufgabenteil a)) zum systematischen Probieren (in Aufgabenteil b)) führt und genutzt wird. (vgl. RLP, S.19)
In diesem Zuge lernen die Schülerinnen und Schüler als dritte Kompetenz:
Die Schülerinnen und Schüler können heuristische Hilfsmittel zum Problemlösen anwenden. (vgl. RLP, S.19)
In dieser Aufgabe werden als heuristische Hilfsmittel die informative Figur (für Aufgabenteil a)) sowie die Tabelle und die Gleichung (für Aufgabenteil b)) angewendet. Als heuristische Strategien lassen sich das Vorwärtsrechnen (in Aufgabenteil a)) und das systematische Probieren (in Aufgabenteil b)) einbringen. Im erweiterten Teil (Aufgabenteil c)) kann schließlich noch das heuristische Extremalprinzip vermittelt werden.
Heuristische Hilfsmittel:
- Die Lösung des Aufgabenteils a) wird begleitet von dem heuristischen Hilfsmittel der Informativen Figur, indem die Zeichnung zunächst in vereinfachter, zweidimensionaler Form abgezeichnet wird. Beim zeichnerischen Lösungsweg wird die informative Figur in allen Aufgabenteilen genutzt.
- In Aufgabenteil b) und c) bei der rechnerischen Lösung wird die Systematik des heuristischen Hilfsmittels Tabelle zunutze gemacht, welche in ähnlichen Aufgaben bereits kennengelernt wurde.
- Außerdem werden bei der Ermittlung des Umpfangs und des Flächeninhalts sowie bei der rechnerischen Ermittlung aller Möglichkeiten für die Umzäunung des neuen Beets Gleichungen verwendet.
Heuristische Strategien:
- Bei Aufgabenteil a) wird für das weitere Vorgehen die heuristische Strategie des Vorwärtsarbeitens genutzt, indem überlegt wird, was gegeben ist und damit weiterarbeitet wird. Dabei werden die Überlegungen geprägt von der heuristischen Strategie der Analogiebildung. Dadurch, dass schon ähnliche Aufgaben bekannt sind, kann sogleich auf die Formel für den Umfang zurückgegriffen werden und es können die Maße für das neu zu erstellende Beet nach den Seitenlängen a und b aufgeteilt und berechnet werden.
- Bei der zeichnerischen Lösung werden die heuristischen Strategien des Vorwärtsarbeitens und des systematischen Probierens benutzt: Zunächst werden alle möglichen Beetvarianten aufgezeichet, indem systematisch die Maße beider ursprünglichen Beete miteinander kombiniert werden. So entstehen in Aufgabenteil b) sechs mögliche Beete, wobei zwei dieselben Maße haben, welche sich jedoch aus unterschiedlichen Zaunstücken zusammensetzten. Dass sich diese doppeln wird daher erst in Aufgabenteil c) ersichtlich. Zur Ermittlung der Flächeninhalte aller sechs Beete werden die Seitenlängen addiert und schließlich multipliziert. Auf diese Weise ist zwar keine Systematik zwischen den Beeten erkennbar, aber der höchste Wert ist unter den Lösungen zu finden. Es werden somit deutlich weniger heuristische Hilfsmittel und Strategien für den Lösungsfindungsprozess verwendet, aber die Bearbeitung der Aufgabe ist dennoch möglich.
- Außerdem wird inbesondere bei Lösungsvariante 3 eine Kombination aus Vorwärts- und Rückwärtsarbeiten genutzt. Zunächst müssen die einzelnen Umfänge der Rechtecke und der Umfang des neuen Rechteckes bestimmt werden (Vorwärtsarbeiten). Anschließend werden aus dem Umfang von die neuen Seitenlängen (, ) ermittelt (Rückwärtsarbeiten).
Heuristische Prinzipien:
- Durch die systematische Auflistung in Aufgabenteil b) bei den rechnerischen Lösungen wird deutlich, dass, wenn die Länge der Seite a kontinuierlich zunimmt und die der Seite b dementsprechend abnimmt, sich die Seiten a und b in der Mitte der Tabelle mit dem gleichen Wert treffen und sich die Zahlenkombinationen der Maße für das neue Beet von da an wiederholen. Auf diese systematische Weise wird das heuristische Extremalprinzip deutlich sichtbar. Diese Erkenntnis lässt sich auch für Aufgabenteil c) nutzen. Denn wenn sich die Zahlenkombinationen wiederholen, wird auch derselbe Flächeninhalt entstehen. Es wird deutlich, dass – gemäß dem Extremalprinzip – die kleinsten Werte für den Flächeninhalt zu Beginn und am Ende der Tabelle stehen, während sich der größte Wert für den Flächeninhalt in der Mitte der Tabelle befindet (vgl. Mathewelt, 2016).
- Bei Aufgabenteil b) wird das Invarianzprinzip verwendet. Der Sachverhalt, der immer gleich bleibt ist bei der rechnerischen Lösung, dass zur Ermittlung jeder Möglichkeit die Umfangsformel genutzt werden muss und, dass bei der zeichnerischen Lösung die Seitenlängen der ursprünglichen Rechtecke immer wieder auf die gleiche Art und Weise neu zusammengesetzt werden.
Die Zaunaufgabe hat nach Cohors-Fresenborg et al bezüglich der zeichnerischen Lösung einen Schwierigkeitsgrad von ** und bezüglich der rechnerischen Lösung einen Schwierigkeitsgrad von ***.
Sprachlogische Komplexität:
Die Sprachlogische Komplexität der Zaunaufgabe entspricht der Stufe 1, da sich aus der Reihenfolge der Sätze keine Rückschlüsse auf die Reihenfolge der zu bearbeitenden Schritte ziehen lassen, die Satzstruktur aber nicht zu komplex ist.
Kognitive Komplexität:
Bei der Zaunaufgabe muss vor der Bearbeitung überlegt werden, wie vorgegangen wird. Bei der Lösung müssen heuristische Hilfsmittel, Prinzipien und Strategien angewendet werden. Darüber hinaus muss bei der Ermittlung der Möglichkeiten für das neue Beet die Bedingung berücksichtigt werden, dass dieses einen Umpfang von 20m haben muss. Aufgrund dieser Aspekte ist die Aufgaben bezüglich der Kognitiven Komplexität auf Stufe 2 anzusiedeln.
Formalisierung von Wissen:
Der rechnerischen Lösung lässt sich der Formalisierung von Wissen die Stufe 2 zuordnen: Die Schülerinnen und Schüler müssen eigenständig symbolische Repräsentationen erbringen, sie müssen die Seitenlängen des neuen Beets mit zwei Variablen (hier: a und b) bezeichnen und mithilfe der Umfangsgleichung die jeweils unbekannte Größe ermitteln. Bei der zeichnerischen Lösung (vgl. Lösungsvariante 4) müssen die Schülerinnen und Schüler lediglich bei Aufgabenteil c) die Flächeninhaltsformel für Rechtecke anwenden. Somit lässt sich dieser Lösungsweg der Stufe 1 zuordnen.
Formelhandhabung:
Die Formelhandhabung entspricht bei der zeichnerischen Lösung der Stufe 0, da hier keine algebraischen Operationen erforderlich sind. Bei der rechnerische Lösung sind einfache Termumformungen erforderlich, somit lässt sich die Formelhandhabung dieser auf Stufe 1 einordnen.
Stufenzuordnung:
Formalisierung von Wissen
Stufe 1
Stufe 2
Formelhandhabung
Stufe 0
Stufe 1
Kognitive Komplexität
Stufe 2
Sprachlogische Komplexität
Stufe 1
Hilfestellungen:
Bei der Lösung der Zaunaufgabe könnte es für die Schülerinnen und Schüler schwierig sein, zunächst zu berücksichtigen, dass der Umfang des neuen Beets der Summe der Umpfänge der alten Beete entsprechen muss. Diesbezüglich können folgende Hilfestellungen gegeben werden.
| Allgemein-strategische Hilfen | Inhaltsorientierte strategische Hilfen | Inhaltliche Hilfen |
| Was ist gegeben? | Mit welcher geometrischen Größe kann die Länge der Begrenzungslinien von ebenen Figuren angegeben werden? | Welchen Umfang muss das neue Beet haben? |
| Veranschauliche dir die Situation mithilfe von Skizzen. | Mit welcher geometrischen Größe lässt sich die Länge des zur Verfügung stehenden Zauns angeben? | Wieviel Meter Zaun stehen für die Eingrenzung des neuen Beets zur Verfügung? |
| Welche Größe des neuen Beets lässt sich aus den gegebenen Informationen ermitteln? | Woraus setzt sich die Länge des neuen Zauns/der neue Zaun zusammen? | Welche Umfänge haben die alten Beete jeweils? Was bedeutet dies für den Umfang des neuen Beets? |
Eine weitere kritische Stelle könnte sein, bei der rechnerischen Bearbeitung des Aufgabenteils b) auf die Idee zu kommen, die Umfangsformel für das neue Beet zunächst mit zwei Variablen für die beiden Seitenlängen aufzustellen und diese dann so umzuformen, dass immer eine Seitenlänge festgelegt werden kann und somit die fehlende ermittelt werden kann. Sollte diese Schwierigkeit auftreten, kann wie folgt reagiert werden.
| Allgemein-strategische Hilfen | Inhaltsorientierte strategische Hilfen | Inhaltliche Hilfen |
| Reflektiere, wie du in Aufgabenteil a) zu einer Lösung gelangt bist. | Kannst du eine Formel aufstellen, mit der du verschiedene Möglichkeiten für Seitenlängen des neuen Beets systematisch durchprobieren kannst? | Stelle eine allgemeine Formel für den Umfang des neuen Beets auf. |
| Verallgemeinere dein Vorgehen aus Teilaufgabe a). | Lassen sich aus dem Umpfang des Beets Aussagen über die Seitenlängen dieses machen? | Welche geometrische Größe ist für das neue Beet bereits festgesetzt? Wie lässt sich diese allgemein noch berechnen? |
| Wie kannst du systematisch vorgehen? Gibt es eine sich wiederholende Vorgehensweise zur Ermittlung der einzelnen Möglichkeiten? | Welche Seitenlängen kann ein Rechteck mit einem Umfang von 20m annehmen? | Lege jeweils eine Seitenlänge des neuen Beets fest und ermittle dann die fehlende Seitenlänge. Wiederhole dies für alle möglichen Seitenlängen. |
Sozialformen:
- Einzelarbeit
Differenzierungsmöglichkeiten:
Differenzierungsmöglichkeiten für leistungsschwächere Schülerinnen und Schüler könnten folgendermaßen aussehen:
- Bei Aufgabenteil a) könnte der Hinweis gegeben werden, die Aufgabe zeichnerisch zu lösen.
- Für Aufgabenteil b) sollte der Hinweis erfolgen, dass beim Aufzeichnen der Beete die Seitenlängen beschriftet und diese Zahlen in eine Tabelle eingetragen werden sollen, sodass die leistungsschwächeren Schülerinnen und Schüler den Überblick behalten, welche Zahlenkombinationen sie bereits ermittelt haben. Außerdem könnte man ihnen bereits verraten, dass es fünf verschiedene Beet-Varianten gibt.
- Für Aufgabenteil c) sollte als Tipp auf die in b) erstellte Tabelle verwiesen werden und, dass nur eine weitere Spalte ergänzt werden braucht, in der der Flächeninhalt eingetragen wird. Somit wissen die Lernenden sogleich, wo sie anknüpfen können und geraten nicht in die Verlegenheit gegebenenfalls mit Spekulationen zu beginnen.
- Leistungsschwächere Schüler und Schülerinnen könnten Streichhölzer o. Ä. zur Verfügung gestellt werden, um das Verständnis für den Umfang von Rechtecken zu erleichtern.
- Zunächst sollten die Eigenschaften von Rechtecken und die Formel zu Berechnung des Umfangs wiederholt werden. Man kann den Schülerinnen und Schülern dann verschiedenfarbige Schnüre geben und sie auffordern die Maße der Beete (evtl. im verkleinerten Maßstab; bei der Umrechnung helfen) zuzuschneiden. Aus diesen Schnüren kann man dann die Rechtecke legen lassen. Die Lösung sollte der Lösung in 2b) entsprechen. Mit der Schnur, die dem ermittelten Gesamtumfang entspricht (20m; evtl. wieder einen anderen Maßstab nutzen) können weitere Rechtecke gefunden werden.
Differenzierungsmöglichkeiten für leistungsstärkere Schülerinnen und Schüler könnten folgendermaßen aussehen:
- Bei Aufgabenteil b) könnte die Zusatzfrage hinzugefügt werden: „Wie kannst du sichergehen, dass du alle Möglichkeiten gefunden hast? Begründe!“ Auf diese Weise reicht zur Bearbeitung der Aufgabe nicht die zeichnerische Vorgehensweise, sondern es ist ein systematisches Vorgehen mittels Tabelle notwendig.
- Als Zusatzaufgabe ließe sich noch folgender Aufgabenteil d) anschließen: „Beim neuen Grundstück hat Emilys Tante die Möglichkeit, das Beet direkt an den Rand des Gartens anzulegen, welcher mit einem Zaun eingegrenzt ist. Wie groß wird das neue Beet, wenn sie den alten Zaun für drei Seiten verwendet, sodass die alten Zäune genau passen? Bestimme alle Möglichkeiten. Mit welchen Maßen entsteht die größtmögliche Fläche.“
Lösung:
- zur Verfügung stehender Draht: \(20m\)
- für die Seitenlängen einer quadratischen Fläche müsste gelten: \(20:3\) (dies ist nicht möglich)
- bei einem rechteckigen Beet müssen zwei Seiten gleichlang sein: \(a=b\) ; \(c=20-a-b\)
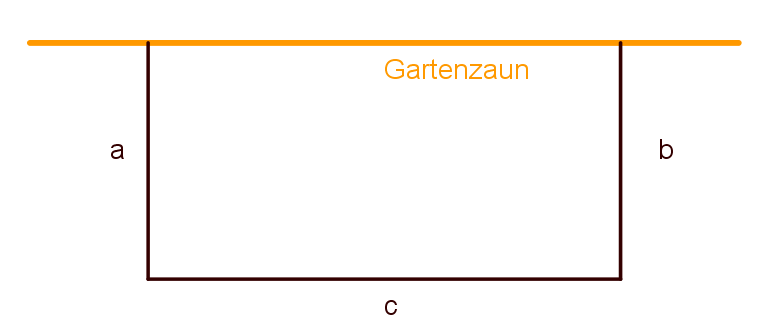
|
Seite a
|
Seite b | Seite c | Flächeninhalt |
| 1 | 1 | 18 | 18 |
| 2 | 2 | 16 | 32 |
| 3 | 3 | 13 | 39 |
| 4 | 4 | 12 | 48 |
| 5 | 5 | 10 | 50 |
| 6 | 6 | 8 | 48 |
| 7 | 7 | 6 | 52 |
| 8 | 8 | 4 | 32 |
| 9 | 9 | 2 | 18 |
Antwort:
Die größtmögliche Fläche entsteht mit den Maßen . Insgesamt gibt es neun Möglichkeiten mit fünf verschiedenen Flächen, den Zaun für das neue Beet zu ziehen.
Hierbei ist es erforderlich, die Aufgabe mit einem neuen Aspekt und somit anderen Angaben neu zu berechnen. Die geistige Beweglichkeit wird also mit einem Aspektwechsel gefördert, indem Aufgabenkriterien variiert wurden (vgl. Kuzle & Bruder (2016)). Die neue Ausgangssituation ist nicht in einer Skizze veranschaulicht, so dass die leistungsstärkeren Schülerinnen und Schüler sich nun selbst das heuristische Hilfsmittel informative Figur anfertigen sollten, um sich den Sachverhalt besser vorstellen und strukturieren zu können (vgl. Mathewelt, 2016). Da alle Möglichkeiten gefunden werden sollen, wird auch eine systematische Herangehensweise nahe gelegt – optimalerweise mithilfe des heuristischen Hilfsmittels Tabelle, das gleich den Flächeninhalt mit einbezieht. Vorab ist die Überlegung sinnvoll, ob sich wieder die größte Fläche bei einer quadratischen Form ergibt. Jedoch lässt sich die zur Verfügung stehende Drahtmenge nicht durch drei teilen, sodass die Schülerinnen und Schüler darauf schließen müssen, dass sich eine rechteckige Fläche ergibt, wobei zwei der gesuchten Seiten gleich lang sind. Mit diesen Vorüberlegungen sollten die Schülerinnen und Schüler errechnen können, dass es neun verschiedene Möglichkeiten der Gestaltung des Beetes gibt, wobei fünf verschieden große Flächeninhalte entstehen. Die größte Fläche ergibt sich mit den Maßen 5 Meter mal 10 Meter gleich 50 Meter.
Diese Zaunaufgabe eignet sich gut für den Einstieg ins Thema, da mit ihr die heuristischen Hilfsmittel sowie einige heuristischen Strategien gut verdeutlicht und vermittelt werden können. So könnte man die Schülerinnen und Schüler die Aufgabe zunächst eigenständig lösen lassen und dann in der Klasse die verschiedenen Lösungsstrategien vergleichen. Anschließend ließe sich aufweisen, welche heuristischen Hilfsmittel und Strategien verwendet wurden und mit welchen die Aufgabe gegebenenfalls leichter hätte bearbeitet werden können. Bezogen auf den systematischen Kompetenzaufbau im Problemlösen ließe sich die Aufgabe sowohl in der ersten Phase der Gewöhnung als auch in der zweiten Phase des Bewusstmachens spezieller Vorgehensweisen anwenden (vgl. MatheWelt, 2016). Es handelt sich um eine typische Beispielaufgabe, anhand derer Lösungswege sich Heurismen erarbeiten lassen, die später als Strategie des Analogieschlusses herangezogen werden können, um vergleichbare Aufgaben mit ähnlichem Vorgehen zu bearbeiten.
Alternativ würde sich die Aufgabe aber auch für das produktive Üben eignen, nachdem die heuristischen Hilfsmittel und die heuristischen Strategien gelehrt wurden. Ein zusätzlicher Arbeitsauftrag dabei wäre, geeignete Heurismen bei der Bearbeitung der Aufgabe zu nutzen. Damit ließe sich die von Kuzle und Bruder (2006) genannte Problemlösekompetenz „Vorgehensweisen und Werkzeuge (Heurismen) zur Bearbeitung geometrischer Fragestellungen zu kennen und situationsgerecht einzusetzen “ (Kuzle, Bruder, 2006, S.3) fördern.
Bearbeitet von: Helen Burchard, Verena Jacob, Jana Proschek, Sarah Ulfig, Sarah Welkisch (überarbeitet von Marisa Pfläging)
nach oben
771 Nutzer/-innen haben abgestimmt.
Feedback
Wir freuen uns auf Ihre Anregungen und konstruktive Rückmeldung zum Material.
Copyright © 2014-2017 - Ana Kuzle
