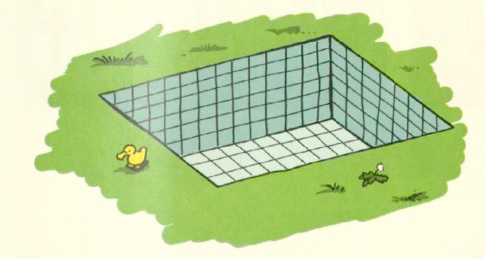
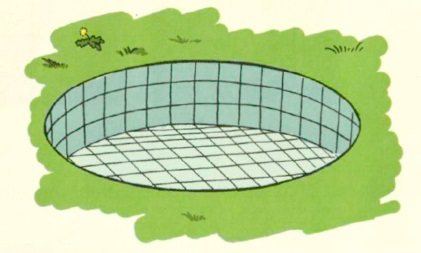
Schwimmbecken

Klasse Schulstufe Thema Themengebiet Schwierigkeit
4 Primarstufe Oberfläche von Quadern Größen und Messen, Raum und Form, Zahlen und Operationen **

Aufgabenstellung

Wie viele Fliesen sind in den Schwimmbecken verklebt?

 

a) Schwimmbecken

Rechne genau.

b) Kinderbecken

Schätze und begründe.

Bildquelle: Abels, L. (2011). Mathepilot (1. Aufl., [Dr.] 1). Stuttgart, Leipzig: Klett. (S.47, Aufgabe 5)

 

Bildquelle: Abels, L. (2011). Mathepilot (1. Aufl., [Dr.] 1). Stuttgart, Leipzig: Klett. (S.47, Aufgabe 5)

 

 

 

Quellenangabe:

Abels, L. (2011). Mathepilot (1. Aufl., [Dr.] 1). Stuttgart, Leipzig: Klett. (S.47, Aufgabe 5)


Lösungsvariante 1 - Rechnerische Lösung
 
 
 
Aufgabenteil a)
 
gegeben:
a = 6 Fliesen
b = 14 Fliesen
c = 8 Fliesen

 

gesucht:

x := Anzahl der Fliesen insgesamt

 

Lösung:

\(x\)

 

 

 

 

\(=2\cdot (a\cdot b)+2\cdot (a\cdot c)+(b\cdot c)\)
\(=2\cdot (6\cdot 14)+2\cdot (6\cdot 8)+(14\cdot 8)\)
\(=2\cdot 84+2\cdot 48+112\)
\(=168+96+112\)
\(=376\)

 

 

Antwort: Im Schwimmbecken sind 376 Fliesen verklebt.

 

 

Aufgabenteil b)
 
Das Kinderbecken sieht gleich lang und gleich breit aus. Allerdings ist es 3 Reihen weniger tief als das Schwimmbecken, welches 6 Reihen tief ist. Also nehme ich die Anzahl der Fliesen im Schwimmbecken und teile sie durch 2, da das Kinderschwimmbecken nur halb so tief ist. Dazu runde ich die Anzahl der Fliesen des Schwimmbeckens von 376 auf 380 auf.
 
Daraus folgt: 380 : 2 = 190
 
 
Antwort: Im Kinderschwimmbecken sind ca. 190 Fliesen verklebt.
 

 

 

 
Lösungsvariante 2 - Zeichnerische Lösung

 

Aufgabenteil a)

Die Wandflächen und Bodenfläche des Schwimmbeckens werden auf Karopapier gezeichnet, wobei eine Fliese einem Kästchen entspricht.

 

Wandflächen:

\(14\cdot 6Fliesen=84Fliesen\quad \)
\(84Fliesen\quad \)
\(8\cdot 6Fliesen=48Fliesen\quad \)
\(48Fliesen\quad \)

 

Bodenfläche:

\(14\cdot 8Fliesen=112Fliesen\quad \)

 

 

Daraus folgt für die Gesamtanzahl A der Fliesen des Schwimmbeckens:

\(A=84+84+48+48+112\\ \quad =168+96+112\\ \quad =376\)

 

Antwort: Im Schwimmbecken sind 376 Fliesen verklebt.

 

 

Aufgabenteil b)

Abschätzung der Wandfläche:

Wird der Radius der Bodenfläche als Hilfslinie eingezeichnet, so kann die Anzahl der Fliesen entlang der halben Beckenkante abgezählt werden. Diese beträgt ungefähr 16 Fliesen. Somit lässt sich die Wand durch zwei Rechtecke der Größe 16 x 3 Fliesen in einer Ebene darstellen.

 

     

 

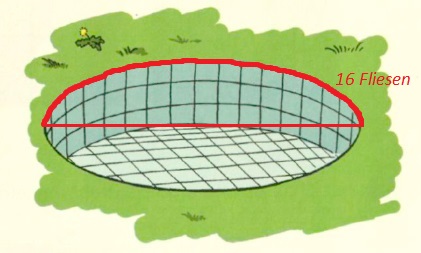
Die Wand des Kinderbeckens besteht also aus ca. \(2\cdot 16\cdot 3Fliesen=96Fliesen\) .

 

Abschätzung der Bodenfläche:

Es lässt sich eine Hilflinie einzeichnen, die den Radius der Bodenfläche darstellt. Durch Abzählen lässt sich eine Länge des Radius von mindestens 13 Fliesen (es lassen sich aufgrund der perspektivischen Zeichnung nicht alle abzählen) erkennen.

 

 

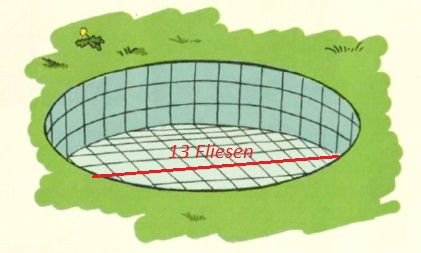
Die Kreisfläche kann mit einem Quadrat der Seitenlänge von 13 Fliesen angenähert werden:          

 

 

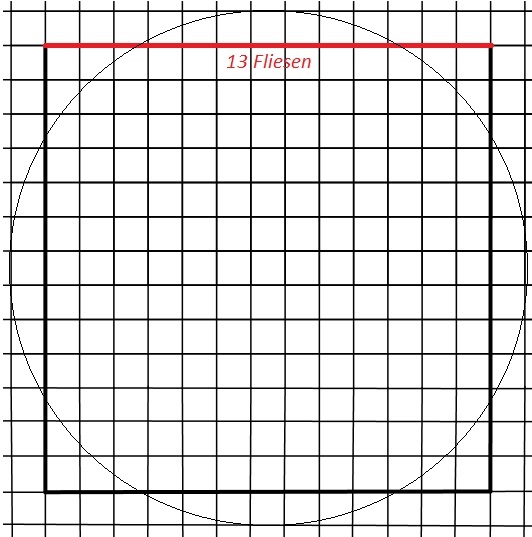
Dieses Quadrat besteht aus \(13\cdot 13Fliesen=169Fliesen\) .

 

Die abgeschätzte Anzahl der Fliesen im Kinderbecken lässt sich nun wie folgt berechnen:

 

\(A=96+169\\ \quad =265\)

 

Antwort: Im Kinderbecken sind ungefähr 265 Fliesen verklebt.

 


Thematisch kann die Aufgabe insbesondere bei der Behandlung von geometrischen Körpern wie Quadern und deren Eigenschaften eingesetzt werden. Bei einer heterogenen Klasse kann diese Aufgabe in Klassenstufe 4 verwendet werden, da die Niveaustufen C und D verschiedener Leitideen angesprochen werden. Ebenso verlangt die Aufgabe von den Schülerinnen und Schülern, dass sie die Multiplikation mit einer einstelligen und einer zweistelligen Zahl beherrschen. Dies ist meist erst in einer vierten Klasse der Fall. Auch der Zahlenraum bis 100 wird überschritten, wodurch der Zahlenraum der Aufgabe die Niveaustufe C der Leitidee „Zahlen und Operationen“ erfordert.


Alle hier formulierten Kompetenzen beziehen sich auf den brandenburgischen „Rahmenlehrplan Teil C Mathematik Jahrgangsstufen 1-10", der ab Schuljahr 2017/18 gültig ist. Mit der Schwimmbecken-Aufgabe werden die inhaltsbezogenen Kompetenzbereiche [L2] Größen und Messen, [L3] Raum und Form und [L4] Gleichungen und Funktionen sowie die prozessbezogenen Kompetenzbereiche [K1] Mathematisch argumentieren, [K2] Probleme mathematisch lösen und [K4] Mathematische Darstellungen verwenden angesprochen (vgl. LISUM 2015).

 

 

Inhaltsbezogene Kompetenzformulierungen

 

Größen und Messen [L2]

Kompetenz 1: Die Schülerinnen und Schüler können den Flächeninhalt bei einem gegebenen, nichtgeradlinigen Rechteck mit Hilfe von Fliesen (Einheitsflächen) berechnen.

"Die Schülerinnen und Schüler können Größen messen [...]" (LISUM 2015, Größenangaben bestimmen, Niveaustufe D, S.24)

Erläuterung: Durch Auszählen der Einheitsflächen, welche bei dieser Aufgabe Fliesen sind, gelingt es den Kindern, den Flächeninhalt der Rechtecke zu bestimmen und somit die Anzahl der Fliesen zu berechnen.

 

Gleichungen und Funktionen [L4]

Kompetenz 2: Die Schülerinnen und Schüler sind in der Lage, die Anzahl der Fliesen insgesamt mit Hilfe einer Gleichung darzustellen.

"Die Schülerinnen und Schüler können Terme und Gleichungen darstellen (auch mit mehreren Rechenoperationen)" (LISUM 2015, Terme und Gleichungen darstellen, Niveaustufe C, S.28)

Erläuterung: Mit Hilfe der ausgezählten Seitenlängen der Rechtecke können die Schülerinnen und Schüler Gleichungen aufstellen, um die Fliesenanzahl der Rechtecke zu berechnen und die Ergebnisse zu addieren. So gelangen sie zur Gesamtanzahl der Fliesen.

 

Raum und Form [L3]

Kompetenz 3: Die Schülerinnen und Schüler sind in der Lage, die Form des Quaders in dem Schwimmbecken zu erkennen.

"Die Schülerinnen und Schüler können ausgewählte geometrische Objekte qualitativ beschreiben" (LISUM 2015, Geometrische Objekte und ihre Eigenschaften beschreiben, Niveaustufe C, S.26)

Erläuterung: Um die Gesamtanzahl der Fliesen zu berechnen, müssen die Schülerinnen und Schüler erkennen, dass das Schwimmbecken die gleichen Eigenschaften wie ein Quader hat. Bei der Berechnung müssen sie beachten, dass
die zwei Seitenflächen jeweils doppelt berechnet werden müssen und die Grundfläche nur einmal.

 

 

Prozessbezogene Kompetenzformulierungen

 

Probleme mathematisch lösen [K2]
Kompetenz 4: Die Schülerinnen und Schüler sind in der Lage, einen geeigneten Lösungsweg zur genauen Berechnung der Fliesenanzahl zu finden.

"Die Schülerinnen und Schüler können Aufgaben bearbeiten, zu denen sie noch keine Routinestrategie haben (sich zu helfen wissen)" (LISUM 2015, S.19)

 

Mathematische Darstellungen verwenden [K4]
Kompetenz 5: Die Schülerinnen und Schüler können die grafische Darstellung des Schwimmbeckens zur Berechnung der Fliesenanzahl verwenden.

"Die Schülerinnen und Schüler können geeignete Darstellungen für das Bearbeiten mathematischer Sachverhalte und Probleme auswählen, nutzen und entwickeln" (LISUM 2015, S.20)

 

Mathematisch argumentieren [K1]
Kompetenz 6: Die Schülerinnen und Schüler sind in der Lage, den Lösungsweg für die Schätzung der Fliesenanzahl des Kinderbeckens zu begründen.

"Die Schülerinnen und Schüler können Begründungen [...] zunehmend selbstständig entwickeln", "mehrschrittige Argumentationen zur Begründung [...] mathematischer Aussagen entwickeln" (LISUM 2015, S.19)

 


Heuristische Hilfsmittel: 
  • Insbesondere in Aufgabenteil a) beim ersten Lösungsweg wird das heuristische Hilfsmittel der Gleichung nach Bruder und Collet (2011) benutzt, indem alle gegebenen Informationen zur Berechnung der gesuchten Information genutzt und in eine selbst aufgestellte Formel eingesetzt werden.

 

  • In der Aufgabenstellung sind durch die skizzenhaften Darstellungen der Schwimmbecken Informative Figuren enthalten. An diesen Skizzen können Lösungsideen erkannt werden. So kann erkannt werden, dass das Schwimmbecken in Aufgabenteil a) die Form eines Quaders hat und bestimmte Längen können mit Hilfe der eingezeichneten Fliesen abgezählt werden. Mit den Skizzen kann auch weitergearbeitet werden, wie durch das Einzeichnen der Hilfslinien in Aufgabenteil b) beim zweiten Lösungsweg besonders deutlich wird.

 

 

Heuristische Strategien: 
  • Beim Ermitteln der Gesamtzahl des Schwimmbeckens wird nach Bruder und Collet (2011) kombiniert rückwärts und vorwärts gearbeitet. Zuerst wird überlegt, was gesucht ist und was dafür benötigt wird. Dabei wird festgestellt, dass zur Berechnung der Gesamtanzahl die Anzahl der Fliesen je Rechteck gebraucht wird, was dem Rückwärtsarbeiten entspricht. Anschließend werden die Seitenlängen der Fliesen ausgezählt und in die Gleichung zur Berechnung der Anzahl pro Rechteck eingesetzt, was dem Vorwärtsarbeiten entspricht.

 

  • Bei der Lösung des Aufgabenteils b) (Lösungsvariante 1) wird durch den Analogieschluss von dem Schwimmbecken aus Aufgabe a) auf das runde Kinderschwimmbecken aus Aufgabe b) geschlossen. Dafür wird die Skizze der Aufgabenstellung genutzt. Die Länge und Breite des rechteckigen Schwimmbeckens kann auf das Kinderschwimmbecken ungefähr übertragen werden. Unterschiedlich ist nur die Tiefe, die bei dem Kinderschwimmbecken drei Reihen beträgt, also die Hälfte der Tiefe des Schwimmbeckens aus Aufgabe a). Um nun die Anzahl der Fliesen im Kinderschwimmbecken zu schätzen, wird die Anzahl der Fliesen des Schwimmbeckens gerundet und anschließend halbiert.

 

 

Heuristische Prinzipien: 
  • Es wird bei der zweiten Lösung von Aufgabenteil a) das Zerlegungsprinzip verwendet: Das Schwimmbecken, welches die Form eines Quaders hat, wird in seine Seitenflächen zerlegt und somit kann zunächst die Anzahl der Fliesen an den Wänden und auf dem Boden des Beckens (mit Hilfe der Flächeninhaltsformel für Rechtecke/durch Abzählen) bestimmt werden. Diese werden letztlich addiert, um die Gesamtzahl der Fliesen im Schwimmbecken zu erhalten.

 

  • Bei der Schätzung der Fliesenzahl im Kinderbecken ist das Invarianzprinzip von Bedeutung. Es wird nach Ähnlichkeiten (die Breite und Länge der beiden Becken) und nach Unterschieden (die Tiefe der Becken) geschaut. Durch diese Feststellungen kann schließlich eine ungefähre Gesamtfliesenzahl im Kinderbecken geschätzt werden. 

Die Schwimmbecken-Aufgabe hat unter Berücksichtigung des Einsatzes in einer vierten Klasse mit vier erreichten Punkten nach Cohors-Fresenborg et al. einen Schwierigkeitsgrad von **.

 

 

Sprachlogische Komplexität: 

Die Sprachlogische Komplexität ist auf Stufe 1 anzusiedeln. Es handelt sich bei den verwendeten Formulierungen zwar um sehr kurze und einfache Hauptsätze, diese geben jedoch keinerlei Auskunft über die Reihenfolge der zu vollführenden Schritte bei der Lösung der Aufgabe.

 

 

Kognitive Komplexität: 

Bei der Bearbeitung der Aufgabe muss zunächst überlegt werden, wie am besten vorgegangen wird. Denkvorgänge sind nacheinander abzuarbeiten, so muss erkannt werden, dass das Schwimmbecken aus Teilaufgabe a) die Form eines Quaders hat, bzw. dass die Wandflächen und der Boden Rechtecke sind, dessen Fliesenanzahlen bestimmt werden können. Nebenbedingungen müssen allerdings nicht berücksichtigt werden, daher hat die Schwimmbeckenaufgabe eine Kognitive Komplexität der Stufe 1 und nicht der Stufe 2.

 

 

Formalisierung von Wissen: 

Zur Lösung der Aufgabe sind einfache Terme aufzustellen, wie bei der ersten Lösung der Teilaufgabe a) die Gleichung zur Berechnung der Gesamtfliesenzahl durch die gegebenen Größen, oder beim zweiten Lösungsweg der Term zur Ermittlung der Gesamtfliesenzahl durch die ermittelten Flächeninhalte der Begrenzungsflächen des Schwimmbeckens. Somit lässt sich auch die Formalisierung von Wissen auf Stufe 1 einordnen.

 

 

Formelhandhabung: 

Auch die Formelhandhabung lässt sich auf Stufe 1 ansiedeln, da bei beiden Lösungswegen Seitenlängen oder Flächeninhalte bloß eingesetzt werden müssen und da lediglich addiert und multipliziert werden muss.

 

 

Stufenzuordnung: 
Formalisierung von Wissen
Stufe 1
Formelhandhabung
Stufe 1
Kognitive Komplexität
Stufe 1
Sprachlogische Komplexität
Stufe 1

Hilfestellungen: 

Für Schülerinnen und Schüler der vierten Jahrgangsstufe könnten an einigen Stellen Schwierigkeiten bei der Bearbeitung auftreten. Hier werden zwei mögliche kritische Stellen genannt und es wird darauf eingegangen, welche allgemein-strategischen Hilfen, welche inhaltsorientierten strategischen Hilfen und welche inhaltlichen Hilfen den Lernenden in solchen Situationen gegeben werden können.

 

Sowohl bezüglich der ersten Lösung als auch bezüglich der zweiten dargestellten Lösung von Aufgabenteil a) ist es relevant, dass die Lernenden die rechteckigen Begrenzungsflächen des Schwimmbeckens erkennen und auf die Idee kommen, die Fliesenanzahlen auf diesen Flächen zu ermitteln. Treten an dieser Stelle Schwierigkeiten auf, so können folgende Hilfen gegeben werden.

 

Allgemein-strategische Hilfen Inhaltsorientierte strategische Hilfen Inhaltliche Hilfen
Was ist gegeben? Erkennst du bestimmte Figuren oder Körper aus dem Unterricht wieder? Welche Länge, Breite und Tiefe hat das Schwimmbecken?
Betrachte die Skizze genau! Lässt sich das Schwimmbecken in bestimmte Teile zerlegen? Wie lässt sich der Flächeninhalt von Rechtecken ermitteln?
Kennst du eine ähnliche Aufgabe aus dem Unterricht? Denke an den Oberflächeninhalt von bestimmten Körpern!

Was kannst du über die Form des Schwimmbeckens sagen?

 Welche Flächen kannst du im Schwimmbecken berechnen?

 

 

Bei der Bearbeitung von Aufgabenteil b) ist es vorteilhaft, wenn die Schülerinnen und Schüler die Form des ersten Schwimmbeckens mit der Form des zweiten Schwimmbeckens vergleichen (wie in Lösungsvariante 1) oder wenn sie die im Kinderbecken auftretenden Flächen mit Flächen vergleichen, die sie bereits berechnen können (wie in Lösungsvariante 2). Sollte den Lernenden hier ein Lösungsansatz fehlen, so können folgende Hinweise helfen die Schülerinnen und Schüler auf einen möglichen richtigen Weg zu leiten.

 

Allgemein-strategische Hilfen Inhaltsorientierte strategische Hilfen Inhaltliche Hilfen
Was ist gegeben? Welche Flächen im Kinderbecken kannst du problemlos ermitteln? Welche (noch) nicht? Haben wir Kreisflächen schon im Unterricht berechnet?
Betrachte beide Skizzen! Kannst du bestimmte Flächen durch ähnliche Flächen ersetzen? Welche Flächen haben wir im Unterricht bereits genau berechnet?
Was ist Gesucht? Wo liegt der Unterschied beim Gesuchten hier zum Gesucht in Aufgabe a)? Vergleiche beide Schwimmbecken! Vergleiche die Seitenlängen der beiden Schwimmbecken miteinander! Was fällt dir auf?

 

 

Sozialformen: 
  • Einzelarbeit
  • Partnerarbeit

 

 

Differenzierungsmöglichkeiten: 

Natürlich kommt die Differenzierung immer auf den geistigen Stand der Kinder an, an die die Aufgabe angepasst wird.

 

Da es vorteilhaft ist, den Kindern gleich designte Aufgaben zu geben, damit ihnen die Differenzierung nicht auffällt und ihr Selbstbewusstsein nicht geschwächt wird, sollte die gleiche Aufgabe für leistungsschwächere Schülerinnen und Schüler verwenden werden, allerdings leicht abgewandelt:

  • Der Zahlenraum, in welchem gerechnet wird, kann verringert werden, indem die Seitenlängen des Schwimmbeckens beispielsweise halbiert werden.
  • Die zusätzliche Abbildung eines Quaders zur Aufgabenbearbeitung kann nützlich sein, da die Lernenden dann direkt vergleichen können.
  • Für Kinder, die eher haptisch lernen, ist es gut, für die Bearbeitung das Modell eines Quaders zur Verfügung zu stellen.
  • Eine weitere Hilfe wäre es, wenn neben dem Schwimmbecken noch eine Körpernetzdarstellung des Beckens zu sehen wäre. So können die Schülerinnen und Schüler direkt erkennen, dass sie beispielsweise die Wände (also die Rechtecke) zweimal zur Berechnung verwenden müssen.

 

Für die leistungsstärkeren Schülerinnen und Schüler gibt es ebenfalls Möglichkeiten die Aufgabe zu verändern, sodass diese anspruchsvoller wird:

  • Die Aufgabenstellung kann erweitert werden, indem die Kinder in einer weiteren Teilaufgabe versuchen sollen, einen weiteren Lösungsweg für die Aufgabe zu finden. Dies soll dazu dienen, dass sie über den von ihnen gewählten Weg reflektieren.
  • Eine weitere Möglichkeit der Veränderung ist es, dass die Lernenden eine ähnliche Aufgabe selbst entwickeln sollen. Dadurch können sie zeigen, dass sie das Prinzip der Aufgabe verstanden haben und sie können das Problem der Aufgabe auf eine ähnliche, ihnen bekannte Situation übertragen (beispielsweise ein Badezimmer mit Fliesen, ein Zimmer mit Tapetenbahnen oder ähnliches).

 


Die Schwimmbecken-Aufgabe eignet sich besonders gut zum Üben der Berechnung von Flächeninhalten von Rechtecken. Da das Schwimmbecken in einzelne Rechtecke zerlegt wird, um die Aufgabe zu lösen, muss die Berechnung von Rechtecken bekannt sein. Durch Nutzung der Formel zur Berechnung der Rechtecke wird der Inhalt hinter der Formel noch einmal verdeutlicht (was ist Seitenlänge a, was ist Seitenlänge b…). Auch das Erkennen verschiedener Körper (in diesem Fall des Quaders) wird durch die Aufgabe noch einmal wiederholt.



Bearbeitet von: Johanna Kwoczek (ergänzt von Marisa Pfläging)
nach oben
473 Nutzer/-innen haben abgestimmt.

Feedback

Wir freuen uns auf Ihre Anregungen und konstruktive Rückmeldung zum Material.