Geometrische Denkaufgabe: Winkeldetektiv 6
| Klasse | Schulstufe | Thema | Themengebiet | Schwierigkeit |
|---|---|---|---|---|
| 6 | Primarstufe | Winkelsätze | Funktionaler Zusammenhang, Größen und Messen, Raum und Form, Zahlen und Operationen | **, *** |
| Heuristsche Hilfsmittel | Heuristische Prinzipien | Heuristische Strategien |
|---|---|---|
| Informative Figur, Gleichungen | Zerlegungs- und Ergänzungsprinzip | Vorwärtsarbeiten, Analogieschlüsse |
Aufgabenstellung
|
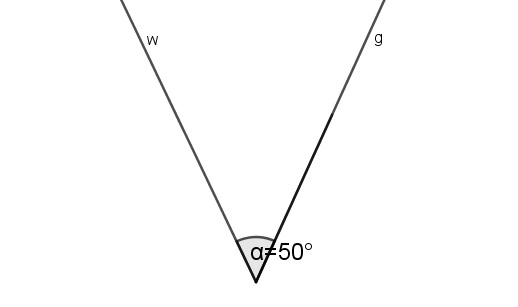
Gegeben ist die folgende Figur mit \(\alpha =50°\). Dokumentiere deinen Lösungsweg in übersichtlicher und gut nachvollziehbarer Form (Bezeichnung deiner Figur, etc.). Begründe deine Schritte!
|
Quellenangabe:
- Lösung
- Themengebiet
- Geförderte Kompetenzen
- Heurismen
- Schwierigkeitsgrad
- Umsetzung im Mathematikunterricht
- Einsatzmöglichkeiten
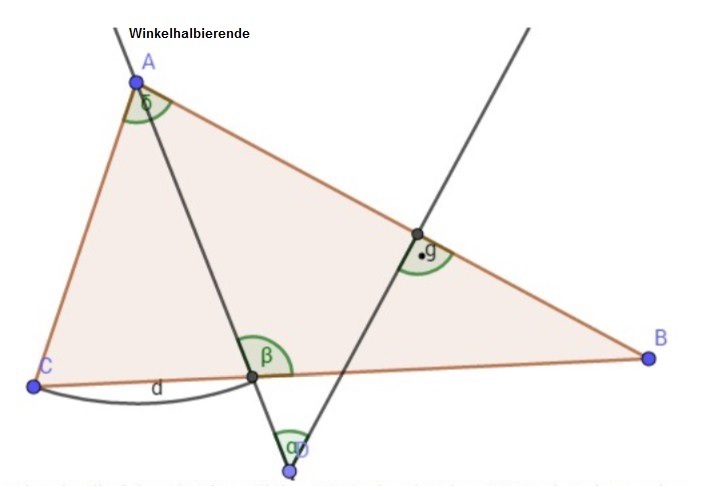
Skizze:
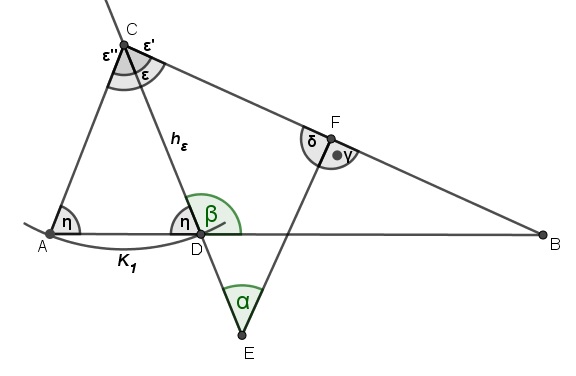
gegeben:
|
Lösungsweg:
|
Mit dem Nebenwinkelsummensatz lässt sich \(\delta \) ermitteln:
|
||||||||
|
Mit der Innenwinkelsumme des Dreiecks \(\Delta CEF\) lässt sich \(\varepsilon '\) ermitteln:
|
||||||||
|
Da die Winkelhalbierende \({ h }_{ \varepsilon }\) den Winkel \(\varepsilon \) in der Hälfte teilt, gilt: \(\varepsilon '=\varepsilon ''\) Da die Punkte \(A\) und \(D\) auf dem Kreisbogen \({ K }_{ 1 }\) um den Punkt \(C\) liegen, gilt \(\overline { CA } =\overline { DC } \) und somit handelt es sich beim Dreieck \(\triangle ADC\) um ein gleichschenkliges Dreieck, das laut Basiswinkelsummensatz zwei gleich goße Basiswinkel \(\eta \) hat. Mit der Innenwinkelsumme für Dreiecke folgt damit
|
||||||||
|
Da \(\beta \) und \(\eta \) zusammen einen gestreckten Winkel ergeben, gilt(/Mit dem Nebenwinkelsummensatz lässt sich nun \(\beta \) ermitteln):
|
||||||||
| Der Winkel \(\beta \) beträgt 110°. |
Skizze:
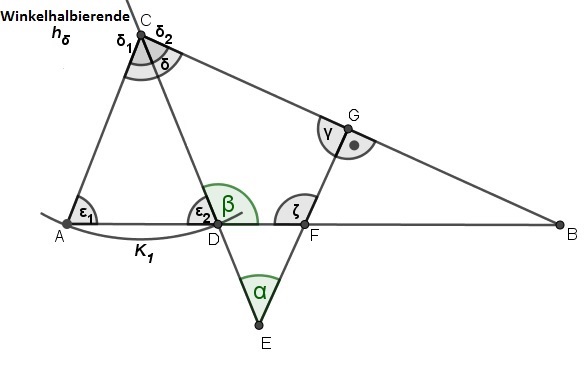
gegeben:
|
Lösungsweg:
| Da es sich beim rechten Winkel um den Punkt \(G\) zusammen mit dessen Nebenwinkel \(\gamma \) um einen gestreckten Winkel handelt, folgt: \(\gamma =90°\) | ||||||||
|
\(\delta \) lässt sich durch Anwendung des Innenwinkelsummensatzes für Dreiecke im Dreieck \(\triangle CEG\) ermitteln:
|
||||||||
| Die Winkelhalbierende \({ h }_{ \delta }\) teilt den Winkel \(\delta \) genau in der Mitte. Somit gilt: \({ \delta }_{ 2 }={ \delta }_{ 1 }=40°\) | ||||||||
|
Da die Punkte \(A\) und \(D\) auf dem Kreisbogen \({ K }_{ 1 }\) um \(C\) liegen, gilt \(\overline { AC } =\overline { CD } \). Somit handelt es sich bei dem Dreieck \(\triangle ADC\) um ein gleichschenkliges Dreieck und mit dem Basiswinkelsatz für gleichschenklige Dreiecke gilt \({ \varepsilon }_{ 1 }={ \varepsilon }_{ 2 }\). Mit der Innenwinkelsumme des gleichschenkligen Dreiecks \(\triangle ADC\) lässt sich nun \({ \varepsilon }_{ 2 }\) berechnen:
|
||||||||
|
Mit der Innenwinkelsumme im Viereck \(AFGC\) lässt sich \(\zeta \) ermitteln:
|
||||||||
|
Mit der Innenwinkelsumme des Vierecks \(CDFG\) lässt sich nun \(\beta \) ermitteln:
|
||||||||
| Der Winkel \(\beta \) beträgt 110°. |
|
Schritt 1: Ich zeichne die Winkelhalbierende \(w\) und trage einen Strahl \(g\) ab, der die Winkelhalbierende unter einem Winkel von \(\alpha = 50°\) berührt. |
|
|
Schritt 2: Ich zeichne einen Punkt \(P\) auf der Winkelhalbierenden ein und fälle das Lot \(h\) von diesem Punkt auf den Strahl \(g\). |
|
|
Schritt 3: Ich messe den Winkel \(\gamma \) zwischen der Winkelhalbierenden \(w\) und dem Lot \(h\) ab. Es ergibt sich ein Winkel von \(\gamma =40°\). |
|
|
Schritt 4: Ich zeichne nun einen Strahl \(f\) unter dem Winkel \(\gamma '=40°\) von der Winkelhalbierenden ein. |
|
|
Schritt 5: Ich ziehe mit dem Zirkel einen Kreisbogen, der den Strahl \(f\) und die Winkelhalbierende \(w\) schneidet. |
|
|
Schritt 6: Ich zeichne einen Strahl \(l\) ausgehend vom Schnittpunkt des Kreisbogens mit \(f\) durch den Schnittpunkt des Kreisbogens mit \(w\). |
|
|
Schritt 7: Ich messe nun den gesuchten Winkel \(\beta \) ab. Es ergibt sich ein Winkel von ungefähr \(\beta =110°\). |
|
Die Aufgabe lässt sich in der sechsten Klasse in der Thematik Winkelsätze anwenden. Die Schülerinnen und Schüler müssen für die Aufgabenlösung die Winkelsätze kennen und flexibel anwenden können. Darüber hinaus müssen die Lernenden bereits Gleichungen lösen können sowie mit Zahlen, Winkelgrößen und der Einheit Grad (°) flexibel umgehen können. Außerdem erfordert die Aufgabe ein flexibles Problemlösen und eine genaue und ausführliche Lösungswegbeschreibung. Alle Aspekte müssen vor der Lösung der Aufgabe schon einmal behandelt worden sein, damit ein eigenständiges Lösen der Aufgabe möglich ist.
Mit der Winkeldetektivaufgabe werden insbesondere die inhaltsbezogene Kompetenzbereich [L3] Raum und Form, [L4] Gleichungen und Funktionen, [L1] Zahlen und Operationen und [L2] Größen und Messen sowie die prozessbezogenen Kompetenzbereiche [K2] Probleme mathematisch lösen, [K1] Mathematisch argumentieren und [K6] Mathematisch kommunizieren aus dem brandenburgischen Rahmenlehrplan (Teil C) Mathematik für die Jahrgangsstufen 1-10 (LISUM, 2015), der ab dem Schuljahr 2017/18 gültig ist, gefördert.
Inhaltsbezogene Kompetenzformulierungen
Die mit der Aufgabe erzielten inhaltsbezogenen Kompetenzen beziehen sich in allen drei Bereichen L3, L4, L1 und L2 auf die Niveaustufe D.
Raum und Form [L3]
Kompetenz 1: Die Schülerinnen und Schüler ermitteln unter Zuhilfenahme von Winkelsätzen und Eigenschaften von Geometrischen Objekten, wie der Winkelhalbierenden eines Winkels, unbekannte Winkelgrößen.
"Beschreiben von Winkelbeziehungen an geschnittenen Geraden bzw. Parallelen sowie in Dreiecken (Scheitelwinkel, Nebenwinkel, Stufenwinkel, Innenwinkel) und Nutzen für Argumentationen" (LISUM, 2015, Beziehungen zwischen geometrischen Objekten beschreiben, Niveaustufe D, S.48), "Erkennen und Beschreiben der Eigenschaften von Winkeln und Dreiecken" (LISUM, 2015, Geometrische Objekte und ihre Eigenschaften beschreiben, Niveaustufe D, S.48)
Erläuterung: Die Schülerinnen und Schüler müssen bei der Lösung der Aufgabe mit Winkelgrößen umgehen können sowie Gebrauch von Winkelsätzen, wie dem Innenwinkelsummensatz oder dem Basiswinkelsatz, machen.
Gleichungen und Funktionen [L4]
Kompetenz 2: Die Schülerinnen und Schüler verwenden Gleichungen zur mathematisch formalen Darstellung des Innenwinkelsummensatzes für Dreiecke, bzw. der Innenwinkelsumme in Vierecken, um unbekannte Winkel in diesen Objekten zu ermitteln.
"Darstellen von [...] innermathematischen Sachverhalten [...] durch Zahlenterme und Gleichungen" (LISUM, 2015, Terme und Gleichungen darstellen, Niveaustufe D, S.54), "Nutzen von Variablen im Sinne eines Platzhalters [...]" (ebd.), "Lösen und Begründen der Lösungen von Gleichungen [...] mit einer Rechenoperation und einem Platzhalter (z. B. mithilfe der Umkehroperation)" (LISUM, 2015, Gleichungen und Gleichungssysteme lösen, Niveaustufe D, S.54)
Erläuterung: In dieser Aufgabe müssen Gleichungen zur mathematischen Darstellung des Innenwinkelsummensatzes für Dreiecke (bei der ersten und zweiten rechnerischen Lösung), bzw. der Innenwinkelsumme von Vierecken (bei der zweiten rechnerischen Lösung) verwendet werden, um fehlende Winkel in einem Dreieck zu errechnen. Dabei findet ein Wechsel von ikonischer (in der Aufgabenstellung gegebene Skizze) zur symbolischen Darstellungsebene statt (dem Winkel ß lässt sich eine Zahl 110(°) als Größenangabe zuordnen). Die Sicherung erfolgt dabei durch die verbale oder mathematisch formale Dokumentation des Lösungsweges im Heft. Eine Voraussetzung für die Lösung mittels Gleichungen ist demnach, dass im vorherigen Unterricht bereits einfache Gleichungsumformungen nach einer Unbekannten thematisiert wurden, was laut LISUM (2015) ebenfalls für die Niveaustufe D vorgesehen ist.
Zahlen und Operationen [L1]
Kompetenz 3: Die Schülerinnen und Schüler lösen Additions- und Subtraktionsaufgaben, um unbekannte Winkelgrößen mithilfe des Innenwinkelsummensatzes zu ermitteln.
"situationsangemessenes Verwenden der Kopfrechenstrategien und der Rechenverfahren" (LISUM, 2015, Rechenverfahren und -strategien anwenden, Niveaustufe D, S.37)
Erläuterung: Da die Schülerinnen und Schüer erst auf der Niveaustufe D die Kompetenz erlangen, "Gleichungen mit einer Rechenoperation und einem Platzhalter (z.B. mithilfe der Umkehroperation) [zu lösen]" (LISUM, 2015, S.54), werden sie bei der Lösung vermutlich so vorgehen, dass sie zuerst die Zahlenwerte in die Gleichung für den Innenwinkelsummensatz einsetzen, die Werte verrechnen und erst dann den Umformungsschritt durchführen, und nicht, wie bei diesen Lösungswegen dargestellt und in der Mathematik eigentlich üblich, erst umformen und dann die Zahlenwerte für die gegebenen Variablen einsetzen.
Größen und Messen [L2]
Kompetenz 4: Die Schülerinnen und Schüler gehen mit der Größe Grad (°) sicher und situationsangemessen um.
"situationsangemessenes Verwenden der Einheiten [...] - auch Grad" (LISUM, 2015, Vorstellungen zu Größen und ihre Einheiten nutzen, Niveaustufe D, S.42), "Zuordnen von Größenangaben zu vertrauten Objekten (Repräsentanten) in [der Einheit Grad]" (ebd.)
Prozessbezogene Kompetenzformulierungen
Probleme mathematisch lösen [K2]
Kompetenz 5: Die Schülerinnen und Schüler erkennen Zusammenhänge zwischen verschiedenen Winkeln mithilfe ihrer Kenntnisse über die Winkelsätze und ermitteln einzelne Winkel wie gewohnt mithilfe dieser Sätze.
"Die Schülerinnen und Schüler können Zusammenhänge erkennen und Lösungsstrategien auf ähnliche Sachverhalte übertragen" (LISUM, 2015, S.19), "Die Schülerinnen und Schüler können mathematische Kenntnisse, Fähigkeiten und Fertigkeiten bei der Bearbeitung von Problemen anwenden" (ebd.)
Erläuterung: Die Schülerinnen und Schüler stehen hier vor einer Aufgabe, deren Lösungsweg ihnen noch nicht bekannt ist. Sie sollen Muster oder Strukturen erkennen (gleichschenkliges Dreieck). Hier wird flexibles Anwenden von Sachverhalten wie den Winkelsätzen aber auch Rechenoperationen erwartet, um auf die Winkelgröße ß zu kommen. Hier werden also verschiedene Heurismen verwendet (vgl. Heurismen).
Mathematisch argumentieren [K1]
Kompetenz 6: Die Schülerinnen und Schüler beschreiben und begründen ihren Lösungsweg kleinschrittig.
"Die Schülerinnen und Schüler können Begründungen [...] zunehmend selbstständig entwickeln" (LISUM, S.19), "Die Schülerinnen und Schüler können mehrschrittige Argumentationen zur Begründung [...] entwickeln" (ebd.)
- In der Aufgabenstellung ist eine Skizze gegeben, die bei der Lösung um weitere Bezeichnungen für Winkel, Punkte und ggf. auch Strecken und Geraden ergänzt wird. An der Skizze können zusammenhänge erkannt werden und die Anwendung bestimmter Winkelsätze wird ersichtlich. Somit wird bei der Lösung der Aufgabe eine Informative Figur genutzt.
- Bei den beiden rechnerischen Lösungswegen werden, je nach Art der Dokumentation (rein inhaltlich, oder mathematisch formal), zusätzlich Gleichungen verwendet.
- Bei den einzelnen Lösungswegen wird vorwärtsgearbeitet. Es wird das Gegebene (die Figur und die gegebenen Winkel) betrachtet und überlegt, welche Teilziele (weitere Winkelgrößen) damit berechnet werden können, um letztendlich den Zielzustand (die gesuchte Winkelgröße) ermitteln zu können.
- Außerdem werden bei der Lösung Analogieschlüsse gezogen. So haben die Lernenden bereits ähnliche Aufgaben gelöst, bei denen sie die Winkelsätze angewendet haben. Auf dieser Grundlage sehen sie Ähnlichkeiten - sogar Analogien - zwischen diesen Aufgaben und der neuen Problemlöseaufgabe und sie wenden diese Fähigkeiten in Teilschritten bei der neuen Aufgabe an.
- Bei der Lösung werden die gesamten Figuren in Teilfiguren (Dreiecke oder Vierecke) zerlegt, in denen dann bestimmte Winkel ermittelt werden. Somit wird das Zerlegungsprinzip angewendet.
Die Winkeldetektivaufgabe hat nach Cohors-Fresenborg et al. hat unter Berücksichtigung des Einsatzes in einer sechsten Klasse bezüglich des ersten und zweiten Lösungsweges mit insgesamt 7 erreichten Punkten einen Schwierigkeitsgrad von *** und bezüglich der zeichnerischen Lösung mit insgesamt 3 erreichten Punkten den Schwierigkeitsgrad **.
Die Aufgabenstellung der Winkeldetektivaufgabe besteht aus einfachen Hauptsätzen. Es werden lediglich Hinweise bezüglich der Lösungsdokumentation gegeben. Der Hinweis, dass die Figur weiter beschriftet werden soll, lenkt die Lernenden möglicherweise durch Analogieschlüsse schon in die Richtung, bestimmte Sätze anzuwenden. Es werden aber keine expliziten Hinweise gegeben, welche weiteren Größen berechnet werden müssen, um zum Ziel zu gelangen, und in welcher Reihenfolge dies geschehen muss. Somit lässt sich die Sprachlogische Komplexität der Aufgabe auf Stufe 1 ansiedeln.
Die Kognitive Komplexität der Winkeldetektivaufgabe entspricht der Stufe 2, da vor der Lösung der Aufgabe überlegt werden muss, wie die Aufgabe gelöst wird und welche Teilziele erreicht werden müssen.
Bei der ersten und zweiten Lösung müssen der Nebenwinkelsummensatz, der Basiswinkelsatz für gleichschenklige Dreiecke und der Innenwinkelsummensatz für Dreiecke und ggf. Vierecke in Form von Gleichungen mathematisch aufgeschrieben werden. Durch selbstständig eingeführte Variablen und Bezeichnungen der in der Skizze gegebenen Größen wird die Lösung übersichtlicher und besser nachvollziehbar. Damit lässt sich die Formalisierung von Wissen beim ersten und zweiten Lösungsweg der Stufe 2 zuordnen. Beim dritten Lösungweg müssen keine Darstellungskontexte erbracht werden. Hier wird die Figur unter Berücksichtigung der Zusammenhänge lediglich nachgezeichnet und der gesuchte Winkel β letztendlich mit dem Geodreieck abgemessen. Bei diesem Lösungsweg entspricht die Formalisierung von Wissen demnach der Stufe 0.
Bei den beiden rechnerischen Lösungswegen müssen Gleichungsumformungen durchgeführt werden. In Anbetracht des Einsatzes der Aufgabe in der sechsten Jahrgangsstufe, in der die Schülerinnen und Schüler erst die Kompetenz erlangen "Gleichungen (auch mit gebrochenen Zahlen) mit einer Rechenoperation und einem Platzhalter (z. B. mithilfe der Umkehroperation) [zu lösen]" (LISUM, 2015, S.54), lässt sich die Formelhandhabung auf Stufe 2 ansiedeln. Bezüglich des zeichnerischen Lösungsweges entspricht hingegen auch die Formelhandhabung der Stufe 0.
Bei der Lösung der Aufgabe können für die Schülerinnen und Schüler an einigen Stellen Schwierigkeiten auftreten. Hier werden zwei solcher kritischen Stellen aufgeführt und es wird darauf eingegangen, welche allgemein-strategischen, welche inhaltsorientierten strategischen und welche Inhaltlichen Hilfen den Lernenden in solchen Fällen weiterhelfen können.
Die Schülerinnen und Schüler könnten Probleme haben, die gegebene Figur in Teildreiecke zu unterteilen und mithilfe des Nebenwinkelsatzes, des Innenwinkelsummensatzes für Dreiecke sowie des Basiswinkelsatzes für Dreiecke fehlende Winkel als Zwischenschritte bei der Ermittlung des gesuchten Winkels β zu berechnen. In diesem Fall können folgende Hinweise gegeben werden.
| Allgemein-strategische Hilfen | Inhaltsorientierte strategische Hilfen | Inhaltliche Hilfen |
| Was ist alles gegeben und was möchtest du ermitteln? | Welche geometrischen Objekte kannst du in der Figur identifizieren? Was weißt du über diese? | Welche Winkel lassen sich bereits mit α und dem rechten Winkel ermitteln? |
| Hast du schon einmal eine ähnliche Aufgabe gelöst, bei der die Figur weniger kompliziert war und bei der mehr Winkel vorgegeben waren? Wie bist du dort vorgegangen? | Kannst du die Figur in Teilfiguren zerlegen? | Was kannst du über den Nebenwinkel des in der Skizze vorgegenen rechten Winkels sagen? |
| Nutze die gegebene Skizze! | Kannst du bekannte Sätze anwenden? | Suche Dreiecke, in denen du den Innenwinkelsummensatz anwenden kannst. |
Außerdem könnte eine besondere Schwierigkeit darin bestehen, von dem gezogenen Kreisbogen auf das in der Skizze gegebene gleichschenklige Teildreieck zu schließen. An dieser Stelle könnten folgende Hilfestellungen gegeben werden.
| Allgemein-strategische Hilfen | Inhaltsorientierte strategische Hilfen | Inhaltliche Hilfen |
| Untersuche, welche Zusammenhänge zwischen den Bestandteilen der Figur/den geometrischen Teilobjekten bestehen. | Kannst du in dem Teildreieck, um dessen Ecken der Kreisbogen gezogen ist, einen bekannten Winkelsatz anwenden? | Was sagt der Kreisbogen über die Seitenlängen des Teildreiecks aus? |
| Welche Bestandteile der Figur/geometrischen Objekte in der Figur kannst du identifizieren? | Welche Information kannst du aus dem gezeichneten Kreisbogen entnehmen? | Welcher Winkel ist in dem Teildreieck mit dem Kreisbogen gegeben? Kannst du mithilfe dieses Winkels die beiden anderen Winkel im Dreieck berechnen? |
| - | Was gilt für den Radius eines Kreises und somit für die beiden Seiten des Teildreiecks, um dessen zwei Ecken ein Kreisbogen gezogen ist? | Um was für ein Dreieck handelt es sich bei dem Teildreieck, um dessen zwei Ecken ein Kreisbogen gezogen ist? |
- Erarbeitung in Einzelarbeit oder in Partnerarbeit
- Vergleich in Partnerarbeit oder im Plenum
Sowohl für leistungsschwächere als auch für leistungsstärkere Schülerinnen und Schüler lässt sich die Aufgabe so abwandeln, dass weder die leistungsschwächeren Lernenden überfordert noch die leistungsstärkeren Lernenden unterfordert sind.
Mögliche Abänderungen der Aufgabenstellung für leistungsschwächere Schülerinnen und Schüler:
- Es können weitere Winkel vorgegeben werden.
|
Beispielaufgabe:
abgewandelte Aufgabenstellung: Gegeben ist die folgende Figur "Alpha" (\(\alpha \)) = 50 Grad (°) und "Delta" (\(\delta \)) = 80 Grad (°). Wie groß ist \(β\)? Dokumentiere deinen Lösungsweg in übersichtlicher und gut nachvollziehbarer Form. Begründe deine Schritte. |
- Als Hinweis oder beiligende Liste (zusätzlich zum Tafelwerk) können Winkelsätze vorgegeben werden, die für die Lösung hilfreich sein können.
Mögliche Abänderungen der Aufgabenstellung für leistungsstärkere Schülerinnen und Schüler:
- Es kann die Zusatzaufgabe gegeben werden, verschiedene Lösungswege zu finden.
- Es kann die Zusatzaufgabe gegeben werden, dass alle restlichen Winkel in der Figur auch berechnet werden sollen. In einem solchen Fall müssen die Schülerinnen und Schüler den Innenwinkelsummensatz für Vierecke zusätzlich betrachten und anwenden (vgl. Lösungsweg 2 - Rechnerische Lösung 2). Der erste Lösungsweg ist dann nicht mehr ausreichend.
Der Einsatz der Aufgabe bietet sich nach der Erarbeitung und Festigung der Winkelsätze an. Dadurch, dass viele Sätze bekannt sein und kombiniert werden müssen, ist diese Aufgabe nicht am Anfang des Themas einsetzbar. Auch für Übungen innerhalb des Themengebietes eignet sie sich nicht, denn die Lösung ist sehr komplex und zeitaufwendig. Diese Aufgabe lässt sich erst am Ende sinnvoll einsetzen, um erlernte Inhalte produktiv zu üben. Denn hier wird ein flexibler Umgang erwartet und die Inhalte müssen selbstständig herangezogen werden.
Bearbeitet von: Lisa Aschendorf, Michelle Buchholz, Laurien Gebhardt (ergänzt von Marisa Pfläging)
Feedback
Wir freuen uns auf Ihre Anregungen und konstruktive Rückmeldung zum Material.
Copyright © 2014-2017 - Ana Kuzle