DIN-A4-Experiment

Klasse Schulstufe Thema Themengebiet Schwierigkeit
8/ 9/ 10 Sekundarstufe I Begründen in der ebenen Geometrie Größen und Messen, Raum und Form *, **

Aufgabenstellung

Mehrere DIN-A4-Blätter sollen wie in der Abbildung wiederholt aufeinandergelegt werden.
 
Was lässt sich entdecken?
Was müsste dafür erfüllt sein?
Warum ist das so?
 
 
 
 

Quellenangabe:

Johnston-Wilder, S. & Mason, J. (Hrsg.) (2005). Developing thinking in geometry. London: SAGE.


Es werden im Folgenden mögliche Lösungswege vorgestellt. In allen Varianten sind die ersten Schritte gleich: Konstruktion durchführen, Vermutung äußern, gesuchten Winkel identifizieren. Im Anschluss wird die Vermutung bewiesen, indem gezeigt wird, dass die entstehenden Innenwinkel stets \(135°\) groß sind. Dabei erfolgt der Beweis entweder durch Rechnung, wobei Wissen über Dreiecke, über Winkelsätze, natürlich über den Satz des Pythagoras oder trigonometrisches Wissen bekannt sein sollte, oder die Symmetrieeigenschaften werden ausgenutzt, die sich durch Falten des Blattes schnell einsehen lassen.
 
  1. Zunächst werden mehrere Blätter wie in der Aufgabe (bzw. Abbildung) beschrieben wiederholt aufeinandergelegt. Bei einigermaßen sorgfältiger Ausführung „landet“ man mit dem neunten Blatt wieder genau auf dem ersten Papier, mit dem man begonnen hatte (oder anders: durch das achte Blatt sollte sich die Figur nun schließen). Betrachtet man nun alle Blätter, ergibt sich eine geometrische Figur aus acht DIN-A4-Papieren – es scheint ein regelmäßiges Achteck entstanden zu sein.
     
  2. Im nächsten Schritt äußert man eine Vermutung: Durch die Konstruktion entsteht ein regelmäßiges Achteck. Hierfür müssten die folgenden zwei Bedingungen erfüllt sein:
    1. alle Seiten sind gleich lang,
    2. alle Innenwinkel sind gleich groß.
​
  1. Alle Seiten sind gleich lang, da es sich um die kürzeren Seiten \(a\) der DIN-A4-Blätter handelt und sich diese nach Konstruktion in einer Ecke berühren. Schwieriger ist das Bestimmen der Innenwinkel, die bei korrekter Vermutung \(\alpha = 135°\) betragen müssten (Winkelsumme in einem n-Eck lautet: \((n-2) \cdot 180°\)).
     
  2. Da ein Teil dieses Winkels bereits aus einem Rechten des zweiten „aufgelegten“ DIN-A4-Papiers besteht, bleiben noch \(\alpha - 90° (=135°-90°=45°)\) „übrig“. Es muss gezeigt werden, dass dieser Winkel \(\alpha-90°\) wirklich \(45°\) groß ist.
 
 
 
Bis hierhin sollte das Vorgehen, wie eingangs erwähnt, einheitlich sein. Der mathematische Beweis beziehungsweise die mathematische Argumentation stellt nun die Problemlöseaufgabe dar. Weiter werden die unterschiedlichen Lösungsschritte der verschiedenen Varianten beschrieben.
 
 
Variante A (Satz des Pythagoras):
 
1. Angenommen, der Winkel \(\alpha-90°\) betrüge \(45°\), dann ergäbe sich in diesem Fall aufgrund der Innenwinkelsumme im Dreieck und des Basiswinkelsatzes (besser dessen Umkehrung) ein gleichschenkliges, rechtwinkliges Dreieck. Zeichnet man ein solches Dreieck ein, ist dabei die kurze Seite des ersten (blauen) Blattes \(a\) eine Kathete, die längere Seite des zweiten (roten) Blattes \(d\) die Hypotenuse und eine Teilstrecke der längeren Seite des ersten (blauen) Blattes \(b\) eine weitere Kathete.
 
2. Kann man nun zeigen, dass dieses Dreieck gleichschenklig ist – dass die Seiten \(a\) und \(b\) übereinstimmen –, so folgt aufgrund des gegebenen rechten Winkels zwischen \(a\) und \(b\), der Innenwinkelsumme und des Basiswinkelsatzes, dass
\((\alpha-90°)+\beta=90°\) und \((\alpha-90°)=\beta\) ist.
                                                             Aus \((\alpha-90°)+(\alpha-90°)=90° \Leftrightarrow (\alpha=135°)\) folgt die Behauptung.

 
3. Im letzten Schritt bleibt daher zu prüfen, ob \(a\) und \(b\) gleich lang sind. Da das normierte Maß eines DIN-A4-Blattes bekannt ist, sind die Seiten \(a\) und \(d\) gegeben. Es gilt sogar \(d= \sqrt2 a\). Im rechtwinkligen Dreieck lässt sich nun der Satz des Pythagoras anwenden und es ergibt sich:
 \(b = \sqrt{{d}^{2}-{a}^{2}}=\sqrt{{(\sqrt{2}a)}^{2}-{a}^{2}}=\sqrt{2{a}^{2}-{a}^{2}}=\sqrt{{a}^{2}}=a\)
 
 
 
 
 
 
 
Variante B (Sinussatz):
 
  1. Man verfährt zunächst wie in Variante A (Satz des Pythagoras) und nimmt an, der Winkel \(\alpha-90°\) betrüge \(45°\). Es ergäbe sich in diesem Fall aufgrund der Innenwinkelsumme im Dreieck und des Basiswinkelsatzes (beziehungsweise dessen Umkehrung) ein gleichschenkliges, rechtwinkliges Dreieck. Dabei ist die kurze Seite des ersten (blauen) Blattes a eine Kathete, die längere Seite des zweiten (roten) Blattes \(d\) die Hypotenuse und eine Teilstrecke der längeren Seite des ersten (blauen) Blattes \(b\) eine weitere Kathete.
     
  2. Nun wendet man den Sinussatz an und stellt folgende Gleichung auf:
\(\frac{d}{\sin 90°}=\frac{a}{\sin \beta}\)
 
  1. Die Seiten \(a\) und \(d\) sind bekannt und es gilt weiterhin, dass sich die Seite \(d\) als \(\sqrt{2}a\) umschreiben lässt. Somit ist
\(\frac{d}{\sin 90°}=\frac{\sqrt{2}a}{1}=\frac{a}{\sin \beta} \Leftrightarrow \arcsin{\frac{1}{\sqrt{2}}}= \beta\) und daher \(\beta=45°\).
 
  1. Wenn \(\beta = 45°\) ist, muss \(\alpha=90°\) aufgrund der Innenwinkelsumme auch \(45°\) sein. Es folgt, dass \(\alpha=135°\) und dass ein regelmäßiges Achteck entsteht.
 
 
Variante C (Definition Sinus):
 
  1. Man verfährt zunächst wie in Variante B (Sinussatz). Im zweiten Schritt wird die Rechnung verkürzt, indem man direkt die Definition des Sinus im rechtwinkligen Dreieck heranzieht. So ist

    \(\sin{\beta}=\frac{a}{d}\) und da \(d=\sqrt{2} a\) gilt: \(\sin{\beta}=\frac{1}{\sqrt{2}}\).


     
  2. Natürlich ergibt sich auch hier, dass \(\beta=45°\) ist, somit \(\alpha=135°\) und dass ein regelmäßiges Achteck entsteht.
 
 
Variante D (Definition Kosinus):
 
  1. Man verfährt zunächst wie in Variante B (Sinussatz). Im zweiten Schritt wird die Rechnung verkürzt, indem man direkt die Definition des Kosinus im rechtwinkligen Dreieck heranzieht. So ist

    \(\cos{\alpha-90°}=\frac{a}{d}\) und da \(d=\sqrt{2} a\) gilt: \(\cos{\alpha-90°}=\frac{1}{\sqrt{2}}\).
     

  2. Mit der Umkehrfunktion des Kosinus ergibt sich, dass \(\alpha-90°=45°\) ist, somit \(\alpha=135°\). Ein regelmäßiges Achteck entsteht demnach.
 
 
Variante E (Symmetrieeigenschaften):
 
 
  1. Will man ein Blatt im DIN-A-Format zu einem Quadrat falten, dessen Seitenlänge der kürzeren Seite des Blattes entspricht, dann faltet man zunächst eine Ecke auf die Längere der beiden Seiten. Die Faltlinie entspricht der Diagonale eines solchen Quadrats.
     
  2. Dass die Faltlinie einen rechten Winkel halbiert ist leicht zu sehen, sie verbindet die eine Ecke des Blattes mit der längeren Seite.​
 
 
 
 
 
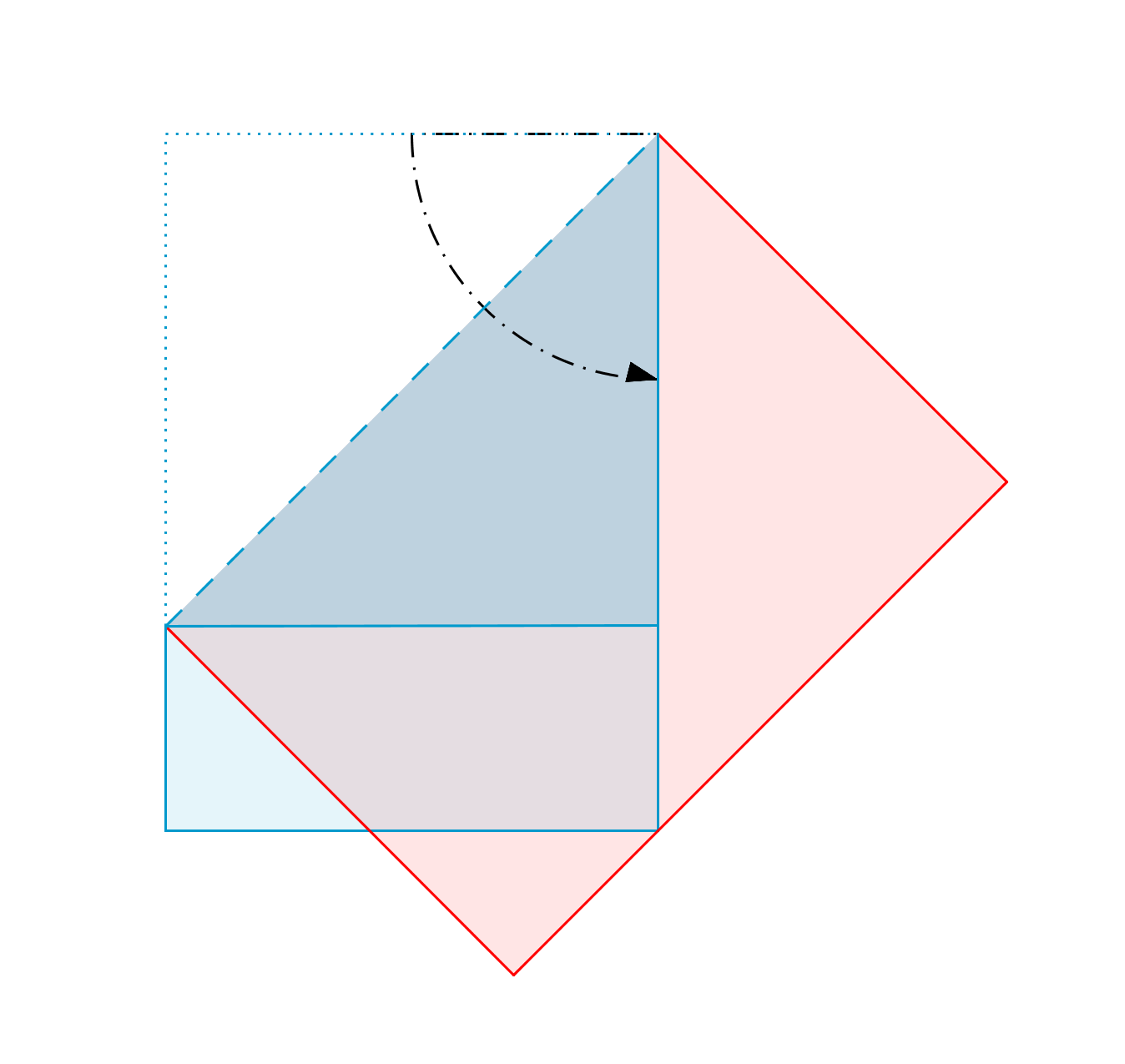
  1. Entspricht die Faltlinie (also die Diagonale des Quadrats) der längeren Seite eines Blattes im DIN-A-Format, dann stimmen die Größen mit denen der Konstruktion überein. \(\alpha-90°\) ist demnach \(45°\) und ein regelmäßiges 8-Eck entsteht.
     
  2. Dass die Faltlinie mit der längeren Seite übereinstimmt, lässt sich rechnerisch zeigen – Satz des Pythagoras, um die Länge der Faltlinie zu bestimmen –, oder indem ein zweites Blatt Papier angelegt wird.
 
 
 
 
 
 
 
Die vorgestellten Lösungswege versuchen auf unterschiedliche Weise, die Größe des Winkels \(\alpha-90°\) zu bestimmen. In Variante A (Satz des Pythagoras) wird eine Strecke ermittelt und die Argumentation läuft auf die Winkelverhältnisse in einem gleichschenkligen Dreieck hinaus. In den darauffolgenden drei Varianten wird Trigonometrie bemüht, um den gesuchten Winkel zu bestimmen. Hervorzuheben ist wohl, dass es keinen Unterschied macht, welchen der beiden unbekannten Winkel im aufgezeigten Dreieck man berechnet, da ein Winkel – nämlich der Rechte – stets durch das rechteckige Papier gegeben ist. In der Variante E (Symmetrieeigenschaften) schließlich werden Symmetrien genutzt, um die Winkelgröße zu beschreiben. Die aufgezeigten Lösungswege lassen sich daher in drei Beweisideen aufteilen, von denen nur eine explizit mit dem Satz des Pythagoras arbeitet.

Die Problemlöseaufgabe steht im Sinne des produktiven Übens und als Beweisproblem eher am Ende einer Unterrichtseinheit zur Satzgruppe des Pythagoras.
 
Die Voraussetzungen des „DIN-A4-Experiments“ unterscheiden sich in den verschiedenen Phasen der Bearbeitung. Zunächst einmal muss die geometrische Figur (regelmäßiges Achteck) als solche erkannt werden und man sollte den mathematischen Begriff „regelmäßig“ kennen. Ist dies erkannt und geklärt, muss man nun konkret wissen, wie groß die Innenwinkel eines regelmäßigen Achtecks sind und wie sich Winkel addieren.
 
Man sollte weiterhin gleichschenklige Dreiecke und den Basiswinkelsatz kennen, sowie die Innenwinkelsumme eines Dreiecks angeben können. Darüber hinaus sollte der Satz des Pythagoras bekannt sein und (auch in anderer Form) zum Errechnen fehlender Seiten beherrscht werden. Für die Bearbeitung des Problems sollten zudem die Seitenlängen der DIN-A-Formate bekannt sein – entweder durch eigene Messung, oder indem die Werte in einer Tabelle angeben werden.
 
Selbstverständlich lassen sich auch trigonometrische Kenntnisse anwenden (siehe Lösung), doch müssen diese nicht vorausgesetzt werden, um das Problem zu lösen. In einer alternativen Beweisidee benötigt man neben dem Wissen über regelmäßige Achtecke Kenntnis über Symmetrieeigenschaften (hier anzuwenden auf Quadrate).
 
 
Wie in den Voraussetzungen angegeben sollte der Satz des Pythagoras bekannt sein (wenngleich anderes mathematisches Wissen ebenso zielführend ist) und die Position innerhalb einer Lerneinheit zum Satz des Pythagoras liegt eher am Ende. Daraus ergibt sich, dass die Aufgabe in Jahrgangsstufe 8 (eher am Ende als am Anfang) eines Gymnasiums anzusiedeln ist. Diese Einbettung ist kohärent mit den Niveaustufen, die sich aus den geförderten Kompetenzen ergeben (Geförderte Kompetenzen).
 
Da die Aufgabe Potential bietet mit anderen mathematischen Mitteln als dem Satz des Pythagoras als grundlegendes Werkzeug bearbeitet zu werden, ist ein Einsatz der Aufgabe zu anderen Zeitpunkten denkbar. So lässt sie sich offensichtlich ebenfalls in Jahrgangsstufe 10 in Zusammenhang mit trigonometrischen Funktionen einsetzen. Die geförderten Kompetenzen bleiben dabei im wesentlichen unberührt, nur dass den Schülerinnen und Schülern mehr Möglichkeiten zur Verfügung stehen, die Aufgabe zu bearbeiten.

Prozessbezogene mathematische Kompetenzen lassen sich für die Aufgaben vor allem in den Standards [K1] Mathematisch argumentieren und [K2] Probleme mathematisch lösen formulieren:
 
  • Die Schülerinnen und Schüler stellen eine Vermutung über die entstehende geometrische Figur auf.
  • Die Schülerinnen und Schüler erkennen Zusammenhänge und Strukturen, indem sie ihr Wissen über Winkel, Dreiecke und den Satz des Pythagoras verknüpfen.
  • Die Schülerinnen und Schüler argumentieren in mehreren Schritten mathematisch, um die Konstruktion des regelmäßigen Achtecks zu begründen.
  • Die Schülerinnen und Schüler entwickeln und nutzen eine Lösungsstrategie, indem sie das Problem auf die relevante Winkelgröße reduzieren.
Die Aufgabe besitzt Beweischarakter, man wird aufgefordert, die geäußerte Vermutung mathematisch zu begründen. Dementsprechend finden sich vor allem in diesem Bereich prozessbezogene mathematische Kompetenzen. Als Problemlöseaufgabe stehen darüber hinaus der Lösungsprozess und die angewendeten Strategien im Vordergrund, woraus sich weitere Kompetenzen ableiten lassen. Die kognitive Aktivierung spielt eine wesentliche Rolle bei der Aufgabe, wodurch implizit die Verknüpfung von Lerninhalten und somit das Erkennen von Zusammenhängen und Strukturen relevant wird.
 
Zusammenfassend steht auf der einen Seite der Anspruch die geäußerte Vermutung mathematisch zu begründen und auf der anderen Seite die Herausforderung eine geeignete Lösungsstrategie zu entwickeln und zu nutzen.
 
 
Relevante inhaltsbezogene mathematische Kompetenzen ordnen sich vor allem den Bereichen [L2] Größen und Messen (vor allem Unterpunkt Rechnen mit Größen) und [L3] Raum und Form (vor allem Unterpunkt Geometrische Objekte). Folgende inhaltsbezogene Kompetenzen werden durch die Aufgabe gefördert:
 
  • Die Schülerinnen und Schüler verwenden den Satz des Pythagoras zur Berechnung von Strecken.
  • Die Schülerinnen und Schüler rechnen mit Winkelgrößen.
  • (Die Schülerinnen und Schüler berechnen Winkelgrößen mithilfe von trigonometrischen Funktionen.)
  • Die Schülerinnen und Schüler führen die angegebene Konstruktionsvorschrift durch, um ein regelmäßiges Achteck aus DIN-A4-Papier zu erhalten.
  • Die Schülerinnen und Schüler begründen, dass die konstruierte Figur ein regelmäßiges Achteck ist, mithilfe von einfachen Winkelsätzen, Sätzen am Dreieck und dem Satz des Pythagoras (oder mithilfe von trigonometrischen Funktionen).
 
Beim Bearbeiten der Aufgabe müssen die Schülerinnen und Schüler Winkel wie Strecken zum einen berechnen und zum anderen mit diesen Größen rechnen. Aus aufgezeigten Lösungswegen (Lösung) ergibt sich, dass hier unterschiedliche Mittel zur Berechnung genutzt werden können. Darüber hinaus ist Wissen über Dreiecke, Winkelsätze oder Symmetrien vonnöten, um die mathematische Begründung zu stützen.
 
Insgesamt muss auf der einen Seite berechnet und gerechnet werden und auf der anderen Seite braucht es mathematisches Wissen, um inhaltlich argumentieren zu können.

Heuristische Hilfsmittel: 
Als heuristisches Hilfsmittel unterstützen vor allem Gleichungen den Lösungsfindungsprozess. Ob es der Nachweis eines gleichschenkligen Dreiecks ist oder die Beziehung der Winkel im Dreieck, Gleichungen helfen hier den Überblick zu behalten. Dazu gehört auch, den Strecken und Winkeln geeignete Bezeichnungen zu geben. Die informative Figur oder der Lösungsgraph sind als heuristische Hilfsmittel ebenfalls denkbar, da man sich zunächst verdeutlichen muss, wonach eigentlich gefragt ist und was einem als mathematisches Wissen für den Lösungsprozess sinnvoll zur Verfügung steht.
 
 
Heuristische Strategien: 
Eine Kombination aus Vorwärts- und Rückwärtsarbeiten ist die präsenteste heuristische Strategie bei der Aufgabe. Dadurch, dass man zunächst eine Vermutung äußert, arbeitet man von dieser ausgehend rückwärts, um die gesuchten Größen zu identifizieren. Ist dies geschehen, arbeit man vorwärts, um die gesuchten Größen zu bestimmen. Je nach Lösungsweg kann es zu weiteren Rückwärtsschritten kommen. Beispielsweise arbeitet man bei Lösung – Variante A (Satz des Pythagoras) zunächst vorwärts und weist das gleichseitige Dreieck nach, ehe man von dort den Schritt zurück auf den ursprünglich gesuchten Winkel geht. Hier zeigt sich die Rückführung von Unbekanntem auf Bekanntes als weitere heuristische Strategie: der Nachweis des regelmäßigen Achtecks erfolgt aufgrund von Aussagen über Dreiecke.
 
 
Heuristische Prinzipien: 
Das Zerlegungs- und Ergänzungsprinzip ist ein wesentliches heuristisches Prinzip, dass bei der Aufgabe zum Tragen kommt. Die Reduzierung des entstandenen regelmäßigen Achtecks auf die beiden „Startblätter“ und die anschließende Zerlegung des Innenwinkels ist eine entscheidende und kritische Stelle. Ohne das Zerlegungsprinzip für die Aufgabe zu nutzen, ist ein Fortschreiten im Lösungsprozess schwer denkbar. Die Zerlegung der beiden Blätter in ein Dreieck mit teilweise bekannten Größen ist ein weiterer Schritt bei der Bearbeitung. Darüber hinaus kann das Invarianzprinzip nützlich sein, wenn man bemerkt oder weiß, dass die Seitenverhältnisse der DIN-A-Formate konstant sind. So lässt sich das Problem übertragen auf ein Papier, dessen kürzere Seite eine Längeneinheit lang ist, wodurch sich einige Rechnungen vereinfachen und man weniger Gefahr läuft mit ungenauen Maßzahlen zu rechnen. Argumentiert man beim Lösungsweg mit Symmetrieeigenschaften (siehe dazu Lösung – Variante E (Symmetrieeigenschaften)) wird offensichtlich das Symmetrieprinzip als Heurismus genutzt.

Sprachlogische Komplexität  
Stufe 0
Kognitive Komplexität
Stufe 2
Formalisierung von Wissen
Stufe 0 bis 2
Formelhandhabung
Stufe 0 bis 1

Für jede Stufe wird ein Punkt vergeben, sodass Aufgaben zwischen 0 und 2 Punkten als leicht (*), zwischen 3 und 5 Punkten als mittel (**) und zwischen 6 und 8 Punkten als schwierig (***) bewertet werden. Der Schwierigkeitsgrad des DIN-A4-Experiments lässt sich somit von * bis ** bewerten.
 
 
Sprachlogische Komplexität: 
Die Aufgabe wird zunächst mit einem einfachen Hauptsatz ohne Nebensatz eingeleitet, in dem beschrieben wird, wie man vorgehen soll. Lediglich der sprachliche Ausdruck „wiederholt aufeinandergelegt“ weist eine höhere Komplexität als die übrigen Formulierungen auf, da man aufgrund des Ausdrucks verstehen muss, wie sich die Konstruktion in der Abbildung fortsetzt. Die Abbildung unterstützt allerdings den Aufgabentext wesentlich. Die anschließenden einfachen Fragen entsprechen der Reihenfolge der Bearbeitung der Aufgabe, obgleich keine konkreten Schritte der mathematischen Bearbeitung genannt werden. Für die „Sprachlogische Komplexität“ wird daher Stufe 0 angegeben.
 
 
Kognitive Komplexität: 
Nachdem die Konstruktion durchgeführt wurde, muss eine Auswahl von Denkvorgängen der Bearbeitung vorausgehen. Dabei entwickeln die Schülerinnen und Schüler zunächst eine Lösungsstrategie bevor sie sich in einer mehrschrittigen Bearbeitung der Lösung nähern. Dabei gibt es für die Bearbeitung kein festes Schema und aus dem Unterricht bekannte Modelle sind nicht leicht erkennbar. Weiterhin müssen die Schülerinnen und Schüler auf verschiedene Heursimen zurückgreifen (siehe Heurismen). Das Merkmal „Kognitive Komplexität“ beinhaltet für die Aufgabe somit Anforderungen auf Stufe 2.
 
 
Formalisierung von Wissen: 
Die Aufgabe erfordert es, die ausgelegten Blätter zu einer geometrischer Figur zu abstrahieren und Winkel- und Seitenbezeichnungen selbstständig einzuführen. Diese werden weder vorgegeben noch werden sie von der Aufgabe impliziert. Darüber hinaus müssen die Beziehungen in Gleichungen und Terme übersetzt werden (insbesondere bei einer Verallgemeinerung), die ebenso nicht vorgegeben sind. Aus diesen Überlegungen ergibt sich für das Merkmal ein Schwierigkeitsniveau auf Stufe 2. Löst man das Problem mit Hilfe der Faltung (siehe dazu Lösung – Variante E (Symmetrieeigenschaften)), so ist wesentlich weniger Abstraktion nötig, die Symbolisierung geschieht eher in graphischer Form und es sind höchstens sehr einfache formale Darstellungen zu erfinden. Vor diesem Hintergrund lässt sich für das Merkmal „Formalisierung von Wissen“ Stufe 0 rechtfertigen.
 
Je nach Lösungsweg ergeben sich demnach hohe oder niedrige Anforderungen für das Merkmal „Formalisierung von Wissen“, sodass sich nicht auf eine Stufe festgelegt werden kann. Das Niveau bewegt sich für dieses Merkmal daher von Stufe 0 bis Stufe 2.
 
 
Formelhandhabung: 
Um die Aufgabe zu lösen, sind Termumformungen in einem überschaubarem Maß erforderlich. Lösungsroutinen werden von den Schülerinnen und Schülern angewendet, sobald der Lösungsweg deutlich zu erkennen ist. Dabei ist kein umfangreiches algebraisches Repertoire vonnöten, so dass in der Regel der Umgang mit Brüchen und Quadratwurzeln ausreicht. Das Merkmal „Formelhandhabung“ beinhaltet für die Aufgabe Anforderungen auf Stufe 1. Wie zuvor nimmt eine Lösung unter Berücksichtigung der Symmetrieeigenschaften eine gesonderte Position ein: Hier sind keine Termumformungen oder algebraische Operationen erforderlich. Dem Merkmal würde man daher Stufe 0 zuschreiben.
 
Insgesamt bewegt sich das Merkmal „Formelhandhabung“ je nach Lösungsweg zwischen Stufe 0 und Stufe 1.
 
 
 
Stufenzuordnung: 
Formalisierung von Wissen
Stufe 0
Stufe 2
Formelhandhabung
Stufe 0
Stufe 1
Kognitive Komplexität
Stufe 2
Sprachlogische Komplexität
Stufe 0

Hilfestellungen: 
Für zwei mögliche kritische Stellen der Aufgabe werden im folgenden Abschnitt jeweils drei passende allgemein-strategische, drei inhaltlich-strategische und drei inhaltliche Hilfestellungen formuliert.
 
Eine mögliche kritische Stelle ist das Identifizieren des relevanten Winkels \(\alpha-90°\), das in einem Schritt mit dem Reduzieren auf die beiden „Startblätter“ angesehen werden kann (siehe Abbildungen bei Lösung).
 
Allgemeine strategische Hilfen:
  • Fertige eine Skizze an, in der du Größen markierst.
  • Überlege dir, welche Größen man kennen müsste und welche Größen dir schon bekannt sind.
  • Gibt es überflüssige Informationen? Welche sind wichtig?
 
Inhaltsorientierte strategische Hilfen:
  • Braucht man alle Blätter, um die Vermutung zu beweisen? Auf welche kommt es an?
  • Kann man hier Größen, Winkel, Strecken sinnvoll zerlegen?
  • Lassen sich die Kanten der DIN-A4-Blätter sinnvoll nutzen?
 
Inhaltliche Hilfen:
  • Wie groß sind die Winkel eines DIN-A4-Blattes?
  • Wie setzen sich die Innenwinkel des Achtecks zusammen?
  • Welchen Teil vom Winkel \(\alpha\) kennst du, welchen nicht?
 
Eine weitere mögliche kritische Stelle ist die Frage, wie sich der \(\alpha-90°\)- Winkel berechnen lässt. Dazu ist es ebenfalls hilfreich, sich ein Dreieck einzuzeichnen (siehe Abbildungen bei Lösung).
 
Allgemeine strategische Hilfen:
  • Kennst du ähnliche Aufgaben, bei denen ein Winkel gesucht ist? Was hat dir dabei geholfen?
  • Welche Größen, Winkel wie Strecken sind unbekannt? Überlege, wie sich diese berechnen lassen.
  • Überlege, was gegeben sein müsste, damit du die Aufgabe weiter bearbeiten kannst.
 
Inhaltsorientierte strategische Hilfen:
  • Markiere bekannte Größen in einer Skizze. Lassen sich bekannte geometrische Figuren erkennen?
  • Kannst du bekannte Sätze zu Dreiecken anwenden?
  • Gibt es hier Größen, Winkel, Strecken die gleich groß sind oder gleich groß sein könnten?
 
Inhaltliche Hilfen:
  • Wie viele Winkel muss ich mindestens in einem Dreieck kennen, um alle Winkel zu kennen?
  • Suche nach einem Dreieck in der Figur. Um welche Art von Dreieck müsste es sich handeln?
  • Wenn zwei Winkel in einem Dreieck gleich groß sind, was muss dann gelten?
 
Unabhängig von den genannten Hilfestellungen für zwei mögliche kritische Stellen ist das Wissen über die Seitenverhältnisse des DIN-A4-Formats essentiell für die Bearbeitung der Aufgabe. Ohne konkret vorzuschlagen, wie sie zum Einsatz kommen soll, unten eine Tabelle der Seitenlängen (in mm) verschiedener DIN-A-Größen.
 
DIN A0
841 × 1189
DIN A1
594 × 841
DIN A2
420 × 594
DIN A3
297 × 420
DIN A4
210 × 297
DIN A5
148 × 210
DIN A6
105 × 148
DIN A7
74 × 105
DIN A8
52 × 74
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
Sozialformen: 
Einzelarbeit
Partnerarbeit
Gruppenarbeit
 
 
Differenzierungsmöglichkeiten: 
Die unter Schwierigkeitsgrad und Hilfestellungen diskutierten Schwierigkeiten lassen sich (für leistungsschwächere Schülerinnen und Schüler) vorbeugen. Durch visuelle Unterstützung und der Vorgabe von Winkel- und Seitenbezeichnungen kann ein Großteil der schwierigkeitsgenerierenden Aufgabenmerkmale im Anforderungsniveau gesenkt werden. Geeignet sind dafür die beiden Grafiken aus Lösung – Variante A (Satz des Pythagoras). Dabei ist jedoch zu bedenken, dass dadurch die zu äußernde Vermutung („Es entsteht ein regelmäßiges Achteck.“) eher nebensächlich wird, implizieren die Grafiken doch, dass es nur darum ginge einen Winkel zu berechnen beziehungsweise dessen Größe nachzuweisen.
 
 
Potential birgt das DIN-A4-Experiment, um weiterführende Fragen zu stellen, zu erforschen, welchen Gesetzmäßigkeiten die Konstruktionsvorschrift folgt, oder um die Frage umzukehren und nach einem Papierformat zu suchen (oder zu entwickeln), das ein regelmäßiges 12-Eck entstehen lässt. Im Sinne des Verallgemeinerns, Analogisierens und Umkehrens als Strategien von Aufgabenvariation sollen hier Differenzierungsmöglichkeiten aufgezeigt werden, die für leistungsstärkere Schülerinnen und Schüler genutzt werden können, und trotzdem ganz allgemein motivieren sollen, sich tiefgründiger mit der Aufgabe zu beschäftigen.
 
 
Verallgemeinern und Analogisieren:
 
Wurde gezeigt, dass für DIN-A4-Blätter mit der vorgegebenen Konstruktion ein regelmäßiges Achteck entsteht, so stellt sich die Frage, ob dies mit anderen Papierformaten ebenfalls möglich ist. Wie sieht es für die Formate DIN-A5, DIN-A6 oder DIN-A7 aus? Und was passiert bei Durchführung der Konstruktion mit größeren Blättern in den Formaten DIN-A3 bis DIN-A0? Ist bekannt, dass die Seitenverhältnisse aller DIN-A-Formate gleich ist, so lässt sich die Frage leicht beantworten. Warum somit beim DIN-A-Format bleiben? Was passiert, wenn man dieselbe Konstruktionsvorschrift mit anderen genormten Formaten durchführt? Was passiert bei Umschlägen im DIN-B-Format und was bei normierten Briefumschlägen? Eine Vermutung wäre sicherlich, dass andere n-Ecke entstehen. In diesem Zusammenhang kann man über eine Umkehrung der Fragestellung nachdenken.
 
 
Umkehren:
 
Um mit der bekannten Konstruktionsvorschrift ein regelmäßiges Achteck zu legen, braucht es Blätter (oder Rechtecke), deren Seiten im Verhältnis \(1:\sqrt{2}\) stehen. Doch wie sieht es mit anderen n-Ecken aus? Eine Umkehrung der Fragestellung könnte lauten: Welches Seitenverhältnis ist (bei gleicher Konstruktion) nötig, wenn ein regelmäßiges 12-Eck entstehen soll? Die Frage nach weiteren Polygonen lässt sich zudem öffnen und man kann zu Folgendem auffordern: Entwirf ein Papierformat, sodass – durch das beschriebene wiederholte Anlegen der Blätter – ein regelmäßiges Vieleck deiner Wahl entsteht.
 
 
Umkehren und Analogisieren:
 
Statt die Frage als solche zu ändern oder zu erweitern, lässt sich über eine analoge Konstruktionsvorschrift nachdenken. So ließe sich beispielsweise Folgendes fragen:
 
 
Mehrere DIN-A4-Blätter sollen wie in der Abbildung wiederholt aufeinandergelegt werden.
Lässt sich etwas entdecken? Warum ist das so?
 
 
Dass hier kein regelmäßiges (und überhaupt kein) Vieleck entsteht, liegt natürlich am sich ergebenden Winkel. Es folgt, dass dies für jedes Papier im DIN-A-Format gilt. Wie bereits als Differenzierungsmöglichkeit vorgeschlagen, könnte man weiter gehend nach einem Format fragen, sodass die Konstruktionsvorschrift zu einem regelmäßigen Polygon führt: Entwirf ein Papierformat, sodass – durch das beschriebene wiederholte Anlegen der Blätter – ein regelmäßiges Vieleck deiner Wahl entsteht.

Das DIN-A4-Experiment eignet sich hauptsächlich zum produktiven Üben und zum Beweisen. Die Problemlöseaufgabe verlangt, dass die Schülerinnen und Schüler mathematisches Wissen verknüpfen und so den Satz des Pythagoras als nützliches Instrument in der Geometrie kennen lernen. Die Aufgabe trägt dazu bei, an ganz unterschiedlichen Stellen geeignet mathematisch zu argumentieren. Dabei reicht die einfache Anwendung des Satzes nicht aus, sondern seine Voraussetzungen und Implikationen für den weiteren Lösungsprozess müssen erkannt, verstanden und richtig eingesetzt werden. Der angesprochene Beweischarakter der Aufgabe findet sich in allen Lösungen, da stets eine Begründung der Vermutung verlangt wird.
 
Neben diesen beiden Haupteinsatzmöglichkeiten hat die Aufgabe Potential mathematisch zu forschen. Weiterführende Fragestellungen, die sich aus der Aufgabe ergeben und für ein Forschen in Frage kämen werden unter Differenzierungsmöglichkeiten beschrieben.


Bearbeitet von: Peter Klöpping
nach oben
1100 Nutzer/-innen (inkl. Dir) haben abgestimmt.

Feedback

Wir freuen uns auf Ihre Anregungen und konstruktive Rückmeldung zum Material.