Fliesenmuster
| Klasse | Schulstufe | Thema | Themengebiet | Schwierigkeit |
|---|---|---|---|---|
| 6 | Primarstufe | Flächeninhalt zusammengesetzter Figuren | Größen und Messen, Raum und Form, Zahlen und Operationen | **, *** |
| Heuristsche Hilfsmittel | Heuristische Prinzipien | Heuristische Strategien |
|---|---|---|
| Informative Figur, Gleichungen | Zerlegungs- und Ergänzungsprinzip, Symmetrieprinzip | Rückwärtsarbeiten |
Aufgabenstellung
Zeichne das Muster im Quadrat vergrößert in dein Heft (Seitenlänge a = 6 cm). \(\frac { 1 }{ 4 } \) von der äußeren Kante ist weiß.

Wie kannst du die farbige Fläche bestimmen? Kannst du sie auch berechnen?
Quellenangabe:
- Lösung
- Themengebiet
- Geförderte Kompetenzen
- Heurismen
- Schwierigkeitsgrad
- Umsetzung im Mathematikunterricht
- Einsatzmöglichkeiten
1. Mit Geodreieck oder Lineal wird eine 6 cm lange Linie abgemessen.

2. Mithilfe des Geodreiecks wird ein rechter Winkel abgetragen. Danach wird erneut eine 6 cm lange Linie gezeichnet.

3. Durch Ergänzung der zu diesen beiden Linien parallelen Linien, an deren Endpunkten, entsteht ein Quadrat mit der Seitenlänge a = 6cm.

4. Die Länge der weißen Strecke x (25% der Außenkante) wird durch Dreisatz ausgerechnet:
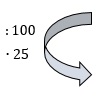 |
100% 25% |
6cm x |
 |
Sie beträgt 1,5 cm.
5. Die beiden Dreiecke an den zwei gegenüberliegenden Eckpunkten des Quadrates werden eingezeichnet. Hierfür werden je 1,5 cm auf den jeweiligen Seiten des Quadrates als Schenkel des rechtwinkligen Dreiecks abgetragen und die Endpunkte dieser Schenkel dann verbunden.
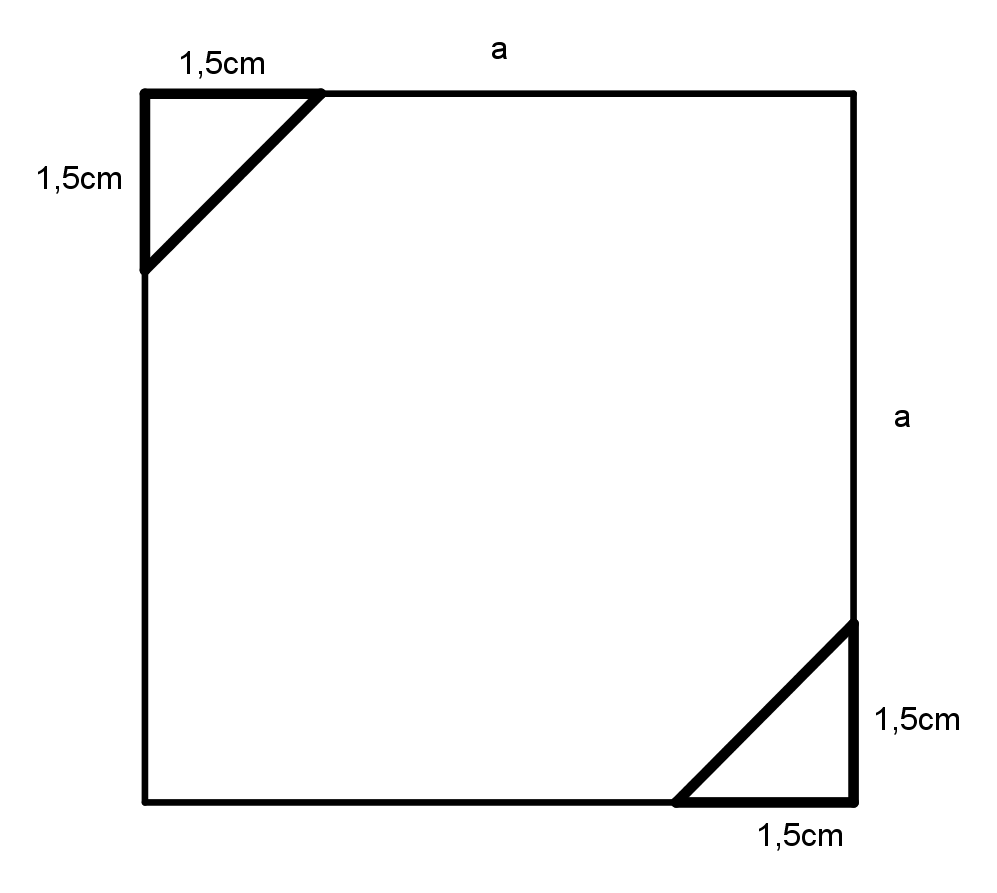
6. Der gelbe Anteil innerhalb des Quadrates wird farbig eingezeichnet.
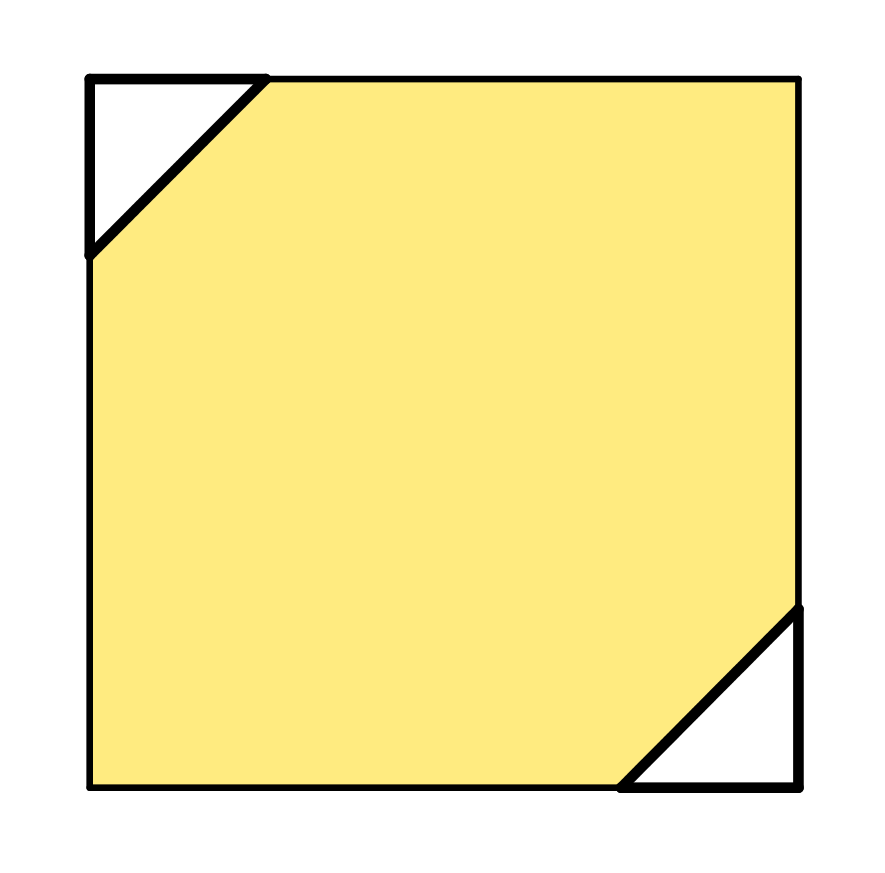
Die Übertragung der Fläche ist abgeschlossen.
Ermittlung der farbigen Fläche
Lösungsvariante 1 - Lösung durch Zerlegung der gelben Fläche in zwei Trapeze
Die farbige Fläche wird in zwei gleich große Trapeze unterteilt.
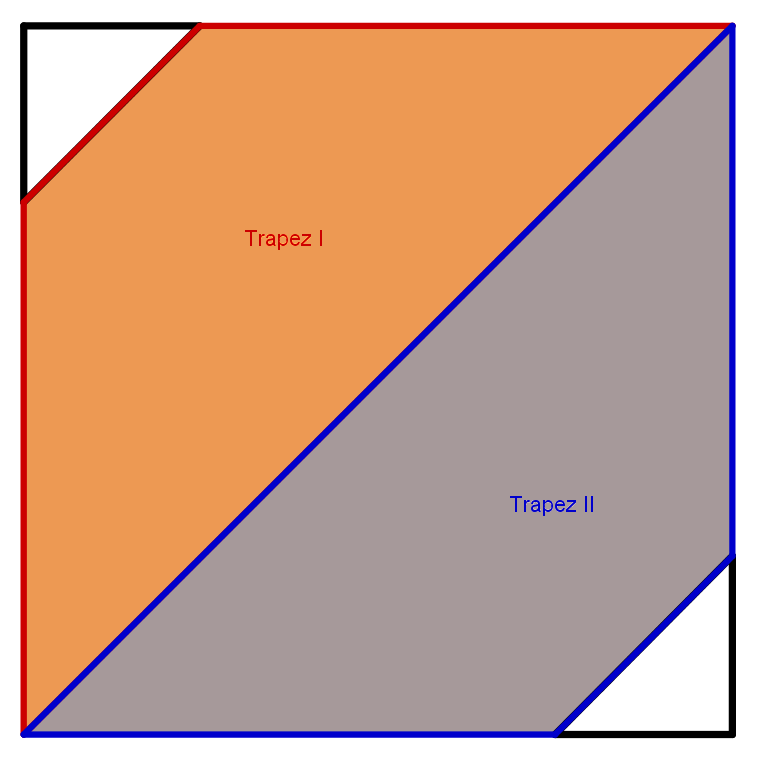
Alle Teilformen sind bekannt und können mit den entsprechenden Formeln ausgerechnet werden:
| großes Quadrat mit der Seitenlänge a=6cm | \({ A }_{ Quadrat }=a\cdot a=6\cdot 6=36[cm²]\) |
| zwei weiße gleich große rechtwinklige, gleichschenklige Dreiecke mit der Kathetenlänge b=1,5 cm | |
| ein rotes und ein blaues Trapez gleicher Größe | \({ A }_{ Trapez }=\frac { 1 }{ 2 } \left( c+d \right) \cdot h\) |
Gesucht ist der Flächeninhalt von Trapez I und Trapez II:
\({ A }_{ farbigeFläche }={ A }_{ TrapezI }+{ A }_{ TrapezII }\)
Ermittle zunächst die Seite d eines Trapezes. Diese entspricht der Diagonalen des Quadrats und lässt sich mit dem Satz des Pythagoras berechnen:

| \(d²=a²+a²\) | |
| \(\Rightarrow \) | \(d²=6²+6²\) |
| \(\Rightarrow \) | \(d=\sqrt { 72 } \approx 8,485[cm]\) |
Ermittle nun die Seite c eines Trapezes. Diese entspricht der Hypothenuse eines der kleinen rechtwinkligen, gleichschenkligen Dreiecke mit den Kathetenlängen von b=1,5cm und lässt sich ebenfalls mit dem Satz des Pythagoras berechnen.
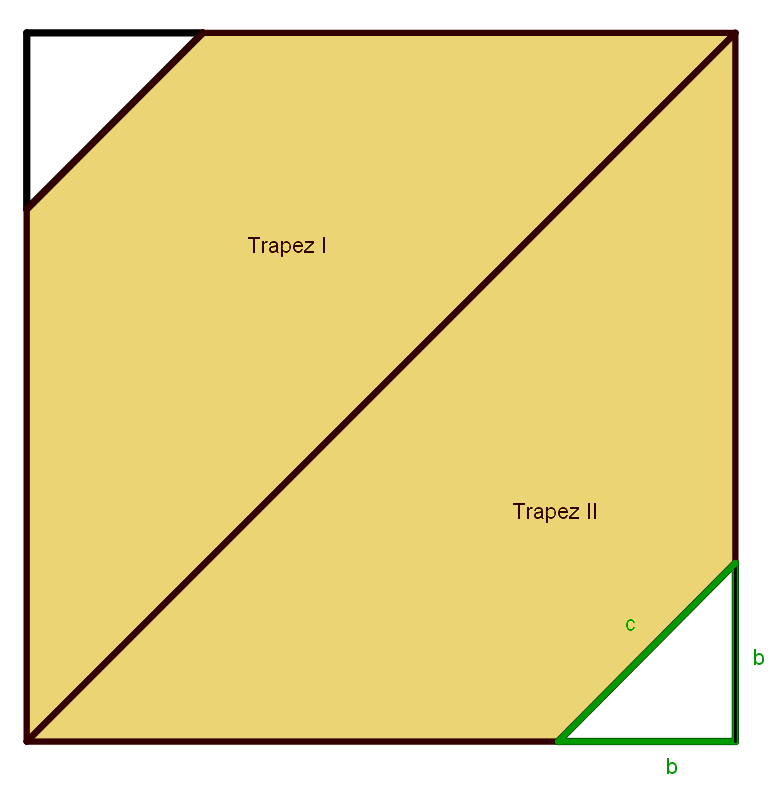
| \(c²=b²+b²\) | |
| \(\Rightarrow \) | \(c²=1,5²+1,5²=4,5\) |
| \(\Rightarrow \) | \(c=\sqrt { 4,5 } \approx 2,12[cm]\) |
Nun fehlt noch die Höhe h des Trapezes. Diese lässt sich wie folgt ermitteln:
\(h=\frac { d }{ 2 } -{ h }_{ \Delta }\)

Es gilt: \(\frac { d }{ 2 } =\frac { 8,485 }{ 2 } \approx 4,24[cm]\)
Ermittle die Höhe des Dreiecks mit dem Satz des Pythagoras:
| \({ h }_{ \Delta }²+{ \left( \frac { c }{ 2 } \right) }^{ 2 }=b²\) | |
| \(\Rightarrow \) | \({ h }_{ \Delta }²+{ \left( \frac { 2,12 }{ 2 } \right) }^{ 2 }=1,5²\) |
| \(\Leftrightarrow \) | \({ h }_{ \Delta }²=1,5²-1,06²\) |
| \(\Rightarrow \) | \({ h }_{ \Delta }\approx 1,06[cm]\) |
Somit ergibt sich für die Höhe h des Trapezes:
\(h\approx 4,24-1,06=3,18[cm]\)
Mit den ermittleten Längen lassen sich nun die Flächeninhalte der beiden Trapeze berechnen:
\({ A }_{ TrapezI }={ A }_{ TrapezII }=\frac { 1 }{ 2 } \left( c+d \right) \cdot h=\frac { 1 }{ 2 } \left( 8,49+2,12 \right) \cdot 3,18\approx 16,87[cm²]\)
\({ A }_{ farbigeFläche }=2\cdot 16,87=33,74[cm²]\)
Die farbige Fläche ist also 33,74 cm² groß.
Lösungsvariante 2 - Lösung durch Ermittlung der Dreiecksflächen

Die Seitenlänge a = 6 cm des großen Quadrates ist bekannt. Der Flächeninhalt kann also berechnet werden. Im nächsten Schritt können die Größen der beiden kleinen Dreiecke davon abgezogen werden, um so den Anteil der gelb markierten Fläche zu bestimmen. Die beiden kleinen gleichschenkligen, rechtwinkligen Dreiecke haben den gleichen Flächeninhalt, da deren Katheten die gleiche Länge haben.
\({ A }_{ farbigeFläche }={ A }_{ Quadrat }-{ A }_{ { \Delta }_{ 1 } }-{ A }_{ { \Delta }_{ 2 } }={ A }_{ Quadrat }-2{ A }_{ \Delta }\)
Berechnung der Fläche des großen Quadrats:
\({ A }_{ Quadrat }=a\cdot a=6\cdot 6=36[cm²]\)
Ermittlung der Flächen der kleinen gleichschenkligen, rechtwinkligen Dreiecke:

Für den Flächeninhalt eines Dreiecks gilt:
\({ A }_{ \Delta }=\frac { g\cdot h }{ 2 } \)
Berechne g mit dem Satz des Pythagoras:
| \(g²=b²+b²\) | |
| \(\Rightarrow \) | \(g²=1,5²+1,5²=4,5\) |
| \(\Rightarrow \) | \(g=\sqrt { 4,5 } \approx 2,12[cm]\) |
Ermittle h mit dem Satz des Pythagoras:
| \({ \left( \frac { g }{ 2 } \right) }^{ 2 }+{ h }^{ 2 }=1,5²\) | |
| \(\Rightarrow \) | \(1,06²+h²=1,5²\) |
| \(\Rightarrow \) | \(h=\sqrt { 1,5²-1,06² } \approx 1,06[cm]\) |
Es ergibt sich für eine Dreiecksfläche:
\({ A }_{ \Delta }=\frac { 2,12\cdot 1,06 }{ 2 } \approx 1,12[cm²]\)
Damit lässt sich die farbige Fläche berechnen:
\({ A }_{ farbigeFläche }=36-2\cdot 1,12=33,76[cm²]\)
Nach diesem Lösungsweg beträgt der Flächeninhalt der gelb markierten Fläche 33,76 cm². Die Abweichung von 0,02 cm² im Vergleich zum ersten Lösungsweg ist auf einen Rundungsfehler zurückzuführen.
Orientiert man sich an den Komponenten der einzelnen Niveaustufen, verteilt über die Jahrgänge in der Grundschule (vgl. LISUM 2015: Rahmenlehrplan Mathematik. Jahrgangsstufen 1-10), und vergleicht diese mit den Leistungsanforderungen der Aufgabe, kommt man zu dem Schluss, dass die sechste Klassenstufe die für diese Aufgabe angemessene ist.
[L2] beschreibt in der Niveaustufe D bezüglich den Vorstellungen zu Größen und ihren Einheiten, dass der Flächeninhalt mit entsprechender Einheit genutzt werden soll. Beim Bestimmen der markierten Fläche ist dies also Voraussetzung. Auch wird unter „Rechnen mit Größen“ bei der für Jahrgangsstufe 6 angestrebten Niveaustufe D gesagt, dass die Schülerinnen und Schüler in der Lage sein sollen, mit den Größenangaben (in diesem Fall also wieder dem Flächeninhalt) zu rechnen. Diese Fähigkeit benötigen sie, wenn sie Teilstücke des Quadrates voneinander abziehen, addieren oder ins Verhältnis zueinander setzen. Auch [L3] (Raum und Form) nennt für die Niveaustufe D einen passenden Arbeitsschritt. Die Lernenden sollen ebene geometrische Figuren zeichnen, was sie beim Übertragen der Darstellung in ihr Heft für das Quadrat und das Dreieck erledigen müssen.
Zu guter Letzt müssen sich die Schülerinnen und Schüler, eine neue, für sie unroutinierte Rechenstrategie erschließen und dabei die Grundrechenoperationen der Addition bzw. Subtraktion einsetzen. Beide Kompetenzen werden zwar bereits ab geringeren Jahrgangsstufen vorausgesetzt, sollen jedoch an dieser Stelle noch einmal die Komplexität der Aufgabe beschreiben. Abschließend lässt sich deshalb sagen, dass Lernende der sechsten Jahrgangsstufe in der Lage sein sollten, die vielen Teilgebiete zusammen zu fügen und so die Aufgabe zu bewältigen. Auch die benötigten heuristischen Arbeitsstrategien sollten in dieser Klassenstufe bereits genügend etabliert worden sein, um nun von den Schülerinnen und Schülern selbstständig eingesetzt werden zu können.
Mit der Aufgabe Fliesenmuster werden die folgenden inhaltsbezogenen und prozessbezogenen Kompetenzbereiche (vgl. LISUM 2015) angesprochen.
| angesprochener inhaltsbezogener Kompetenzbereich | Begründung |
| [L1] Zahlen und Operationen | Zur Bearbeitung der Aufgabe müssen die Schülerinnen und Schülern bereits eine konkrete Vorstellung von natürlichen Zahlen und den Grundrechenoperationen besitzen. Das Rechnen in Kontexten, hier die Bestimmung eines Fliesenausschnitts, erfordert das Verständnis von Zahlen sowie die Erkenntnis, dass die Addition bzw. Subtraktion einzelner Teilstücke der Fliese, zum gewünschten Ergebnis führen kann. |
| [L2] Größen und Messen | Diese Leitidee wird von der Aufgabe angesprochen, da sich die Kinder bei der Bearbeitung im handelnden Umgang mit Größen, Längen, Flächen und in diesem Zusammenhang auch mit Einheiten befinden. Gesucht wird der Flächeninhalt einer Fläche, gegeben sind bereits einige Längenangaben der Fliesenseiten sowie Längenverhältnisse. Diese Informationen müssen dementsprechend weiter verarbeitet werden, um am Ende zu einem Ergebnis zu gelangen. Durch den Realitätsbezug der Fliese wird den Schülerinnen und Schülern hierbei auch klar gemacht, dass Größen etc. auch im alltäglichen Leben eine Rolle spielen. |
| [L3] Raum und Form | Kenntnisse über die Eigenschaften geometrischer Objekte (die Aufgabenstellung setzt bereits das Begriffsverständnis eines Quadrates voraus), über den Umgang mit Figuren in einer Ebene und die Herstellung einer eigenen Skizze werden gefordert. Durch die Zerlegung des Quadrates in Teilstücke zur Herstellung des Fliesenmusters müssen die Kinder bei der Bearbeitung der Aufgabe die einzelnen Teilobjekte in Beziehungen zueinander setzen. |
| angesprochener prozessbezogener Kompetenzbereich | Begründung |
| [K1] Mathematisch argumentieren | Die Aufgabenstellung spricht die Schülerinnen und Schüler direkt an und fragt nach Lösungsmöglichkeiten. Da das Beschreiben und Begründen von Lösungswegen ein Teil des mathematischen Argumentierens ist, wird auch dieser Kompetenzbereich in der Aufgabe angesprochen. |
| [K2] Probleme mathematisch lösen | Die Schülerinnen und Schüler sollen Möglichkeiten entwickeln, den Anteil der markierten Fläche zu bestimmen und auszurechnen. Hierbei sollen sie einen bis dahin unbekannten Lösungsweg entwickeln und gleichermaßen Vermutungen und Zusammenhänge aufstellen und erkennen. Hierfür können sie heuristische Strategien einsetzen, da die Aufgabenstellung keinen konkreten Weg bzw. kein konkretes Vorgehen zum Lösen impliziert. |
| [K4] Mathematische Darstellungen verwenden | Das "Fliesenmuster" ist in einer grafischen Skizze dargestellt. Die Schülerinnen und Schüler können zur Bearbeitung der Aufgabenstellung weitere Skizzen anfertigen, sie können die gegebene ergänzen bzw. sollen eine gleiche Skizze mit gegebenen Maßen in ihr Heft übertragen. Dieses Anfertigen und Interpretieren mathematischer Darstellungsformen fällt in den Kompetenzbereich [K4]. |
| [K5] Mit symbolischen, formalen, technischen Elementen der Mathematik umgehen | Zum Lösen der Aufgabe, müssen die Schülerinnen und Schüler ein angemessenes Verfahren auswählen. Unabhängig davon, auf welche Art genau sie die Lösung ansetzen, müssen spätestens zum Berechnen des Flächeninhalts die passenden Formeln zur Flächeninhaltsberechnung von Figuren abgerufen werden. |
| [K6] Mathematisch kommunizieren | Zur Erfüllung von [K6] bietet die Aufgabe zwar das grundsätzliche Potenzial, jedoch impliziert die Aufgabenstellung alleine noch nicht die Erfüllung dieser prozessbezogenen mathematischen Kompetenz. Sicherlich greift die schriftliche Kommunikation zu gewissen Teilen, nämlich dann, wenn die Schülerinnen und Schüler ihren Lösungsweg nachvollziehbar und strukturiert aufschreiben sollen, jedoch muss die Lehrkraft die Aufgabe konkret für Partner- oder Gruppenarbeit "freigeben" bevor der Anlass zu verstehendem Zuhören oder anderen Aspekten dieses Bereichs gegeben ist. |
Mit der Fliesenmuster-Aufgabe werden die folgenden inhaltsbezogenen und prozessbezogenen Kompetenzen gefördert.
Inhaltsbezogene Kompetenzformulierungen
Zahlen und Operationen [L1]
Kompetenz 1: Die Schülerinnen und Schüler sind in der Lage, Rechenstrategien, -verfahren, -regeln und die Gesetze über additive und subtraktive Handlungen zu nutzen, um die Größen der einzelnen Teilstücke zu errechnen und so den gesuchten Flächeninhalt zu erhalten.
"Die Schülerinnen und Schüler können Rechenstrategien, -verfahren, -regeln und Gesetze der Grundrechenoperationen nutzen" (LISUM 2015, Rechenverfahren und -strategien anwenden, Niveaustufe D, S.23)
Begründung: Damit die Schülerinnen und Schüler auf die Längen und Flächeninhalte der markierten Fläche kommen, müssen sie zuvor die Angaben der angrenzenden Teilstücke ausrechnen. Betrachten wir beispielsweise den zweiten Lösungsweg als Beispiel, so müssen hier die Längen der beiden kleinen Dreiecke, deren Flächeninhalt und anschließend auch die Größe des gesamten Quadrates bekannt sein, um dann durch die Subtraktion der kleinen Dreiecke auf die gelb markierte Fläche zu kommen.
Größen und Messen [L2]
Kompetenz 2: Die Schülerinnen und Schüler sind in der Lage mit Längen und Flächeninhalten zu rechnen, und die zusammengesetzten Größen der geometrischen Figuren Quadrat und Dreieck zu bestimmen.
"Die Schülerinnen und Schüler können mit Größenangaben rechnen (auch mit Flächeninhalten [...])" (LISUM 2015, Größen in Sachzusammenhängen berechnen, Niveaustufe D, S.25)
Begründung: Die Inhaltsbezogene Kompetenz "Rechnen mit Größen" , setzt die Fähigkeit Größen in Sachzusammenhängen zu berechnen voraus. Hierfür wird bereits auf Niveaustufe B damit begonnen, mit Längen zu rechnen. Dies muss zur Bestimmung der Seitenlängen der Dreiecke in unserer Aufgabe erfolgen. Die Kompetenz mit Flächeninhalten zu rechnen, wird ab Niveaustufe D ebenfalls verlangt. Diese Fähigkeit wird bei der Musterlösung ebenfalls benötigt, da die Kinder den Flächeninhalt des Mittelstücks des Quadrates ausrechnen sollen. Damit dies gelingt, müssen die Möglichkeiten zur Flächeninhaltsbestimmung von Quadraten, Dreiecken sowie gegebenenfalls Trapezen (siehe Lösungsweg 1) bekannt sein und umgesetzt werden können.
Raum und Form [L3]
Kompetenz 3: Die Schülerinnen und Schüler sind in der Lage, die ausgewählten geometrischen Objekte Quadrat und Dreieck zu zeichnen.
"Die Schülerinnen und Schüler können ausgewählte geometrische Objekte herstellen und zeichnen" (LISUM 2015, Geometrische Objekte darstellen, Niveaustufe B, S.26)
Begründung: Unter der dritten Leitidee "Raum und Form" wird von den Kinder ab Klasse 2 (Niveaustufe B) unter dem Aspekt "Geometrische Objekte darstellen" die zeichnerische Anfertigung geometrischer Grundfiguren gefordert. Unsere bearbeitete Problemlöseaufgabe fordert von den Schülerinnen und Schülern die Anfertigung einer vergrößerten Skizze der dargestellten Fliese. Das Quadrat ist durch Linien in zwei Dreiecke unterteilt, demzufolge müssen die Kinder ein Quadrat sowie zwei Dreiecke zeichnen, um das Muster in ihr Heft zu übertragen.
Prozessbezogene Kompetenzformulierungen
Probleme mathematisch lösen [K2]
Kompetenz 4: Die Schülerinnen und Schüler sind in der Lage, unter Zuhilfenahme ihrer mathematischen Kenntnisse bezüglich der Flächeninhaltsbestimmung und den Eigenschaften geometrischer Figuren, die Aufgabe zu lösen, zu der sie noch keine Routinestrategie kennen.
"Die Schülerinnen und Schüler können Aufgaben bearbeiten, zu denen sie noch keine Routinestrategie haben (sich zu helfen wissen)", "können mathematische Kenntnisse, Fähigkeiten und Fertigkeiten bei der Bearbeitung von Problemen anwenden" (LISUM 2015, S.19)
Begründung: Die Kompetenz "Probleme mathematisch lösen" bezieht sich auf die Fähigkeit der Schülerinnen und Schüler, Aufgaben zu lösen, zu denen sie noch keinen routinierten Lösungsweg kennen. Damit dies gelingt, müssen sie in der Lage sein, ihr sonstigen Vorwissen zu aktivieren und auf den aktuellen Sachverhalt passend anzuwenden. In der hier behandelten Aufgabe müssen die Kinder erkennen, dass es sich um eine geometrische Figur handelt, die in Teilstücke zerlegt wurde. Außerdem muss bewusst sein, dass man mittels dem Messen bzw. Ausrechnen bestimmter Längen, mit den
dazugehörigen Formeln den Flächeninhalt ausrechnen kann und so zu einer Lösung des Problems gelangen kann. Das aktive Auseinandersetzen mit der Aufgabe an sich sowie mit geometrischen Sachverhalten muss erfüllt sein, damit die Lösung des Problems erarbeitet werden kann und eine Lösungsstrategie entsteht.
Mathematische Darstellungen verwenden [K4]
Kompetenz 5: Die Schülerinnen und Schüler sind in der Lage, die relevanten Informationen aus der grafischen Darstellung zu entnehmen, um eine entsprechende neue Skizze anzufertigen.
Kompetenz 6: Die Schülerinnen und Schüler sind in der Lage, eine vorgegebene Skizze zielgerichtet unter Beachtung der gegebenen Seitenlängen und Verhältnissen einzelner Teilstücke, in eine weitere grafische Darstellung zu übernehmen und entsprechend zu verändern.
"Die Schülerinnen und Schüler können Darstellungen zielgerichtet verändern", "können eine Darstellung in eine andere übertragen", "können Darstellungen bewerten oder interpretieren" (LISUM 2016, S.20)
Begründung: Die Prozessbezogene Kompetenz "Mathematische Darstellungen zu verwenden" nennt die Komponente "Darstellungen zielgerichtet verändern". Die Darstellungsebene wird in unserer Aufgabe nicht übersetzt, die Schülerinnen und Schüler sollen lediglich die grafische Skizze vergrößert in ihr Heft übertragen. Damit dies gelingt, müssen sie die gegebenen Informationen bezüglich der vergrößerten Darstellung entsprechend auf die Ausgangsskizze übertragen und verändert einzeichnen. Hierbei erfüllen sie einen weiteren Aspekt des mathematischen modellierens. Sie entnehmen die relevanten Informationen aus der Aufgabenstellung sowie der beigefügten Skizze und führen die gegebenen Informationen zusammen. Nur wer die Angabe "1/4 der Außenkante ist weiß" auf die Zeichnung des Quadrates übertragen kann, wird in der Lage sein diese Aufgabe zu lösen.
- Als Heuristisches Hilfsmittel hat die gegebene Skizze der Fliese gedient. Diese informative Figur konnte in Verbindung mit den gegebenen Maßen und Verhältnissen anschließend in eine größere Skizze derselben Figur umgewandelt werden.
- Außerdem wurden Gleichungen zum Ermitteln der Kathetenlänge der Dreiecke sowie Gleichungen zum Ermitteln der Flächeninhalte der jeweiligen Figuren, in welche die Fliese unterteilt wurde, genutzt.
- Bei der Problemlöseaufgabe "Fliesenmuster" lässt sich durch Rückwärtsarbeiten eine Lösung finden. Es wird zunächst betrachtet, was gesucht ist und was darüber bereits bekannt ist. Beim Zeichnen der Figur, und dem Abtragen der beiden Eckdreiecke, entsteht die Idee, dass man den Flächeninhalt dieser beiden Teilstücke einfach von dem Gesamtflächeninhalt der Fliese, also dem des Quadrats, abziehen könne. Um diesen Lösungsansatz zu verfolgen, werden im nächsten Schritt die Angaben, die benötigt werden, um die gesuchte Fläche (also die Differenz aus dem Flächeninhalt des Quadrats und den zwei Dreiecken) zu errechnen, betrachtet. Die gegebene Seitenlänge a des Quadrates ist bekannt und so kann mittels der Formel zur Bestimmung des Flächeninhalts eines Quadrates sofort der Flächeninhalt der gesamten Fliese bestimmt werden. Nun fehlt noch die Größe eines Dreiecks, welche man anschließend verdoppeln könnte. Um den Flächeninhalt eines Dreiecks auszurechnen, wird nun also die Grundseite g sowie die Höhe h gesucht. Basierend auf der Frage „Was benötige ich, um das Gesucht zu ermitteln?“ wird als nächster Schritt die durch das vorangegangene Zeichen der Figur bekannten Kathetenlängen der Dreiecke eingesetzt, um anhand dieser Information die Hypotenuse unter Zuhilfenahme des Satzes des Phytagoras auszurechnen. Dadurch ist es dann möglich durch den gleichen Satz die Höhe des Dreiecks zu ermitteln. Schülerinnen und Schüler der sechsten Klasse werden sicherlich die Längen nicht ausrechnen, sondern messen. Dies tun sie jedoch auch erst ab dem Moment, in dem ihnen klar wird, dass sie zur Flächeninhaltsbestimmung der markierten Fläche erst die Größe des Quadrates und der beiden Dreiecke benötigen.
- Beim ersten Lösungsweg wird die gelbe Fläche in zwei gleich große Trapeze zerlegt. Die Berechnung der Flächeninhalte ermöglicht letztendlich die Ermittlung des Flächeninhalts der gelben Fläche. Bei dieser Lösung wird demnach das Zerlegungsprinzip angewandt.
- Außerdem ist das Symmetrieprinzip von Bedeutung, da beim zweiten Lösungsweg die Tatsache genutzt wird, dass es sich um zwei gleich große Dreiecke handelt und beim ersten Lösungsweg, dass die beiden Trapeze den gleichen Flächeninhalt haben.
Die Fliesenmuster-Aufgabe hat unter Berücksichtigung des Einsatzes in einer sechsten Klasse nach Cohors-Fresenborg et al. mit vier erreichten Punkten bei der Lösung ohne Verwendung des Satzes des Pythagoras, bzw. mit sechs erreichten Punkten unter Zuhilfenahme dieses Satzes einen Schwierigkeitsgrad von ** bzw. ***.
Die Fliesenmuster-Aufgabe weist bezüglich der Sprachlogischen Komplexität einen Schwierigkeitsgrad der Stufe 1 auf. Es handelt sich bei der Aufgabenstellung zwar um einfach Hauptsätze, die Reihenfolge der Sätze entspricht jedoch nicht unmittelbar den Schritten der mathematischen Bearbeitung.
Bei der Lösung der Aufgabe müssen Denkvorgänge nacheinander abgearbeitet werden: Die gelbe Fläche kann mittels Hilfsflächen berechnet werden. Bei den Berechnungen der Hilfsflächen (beim ersten Lösungsweg der beiden Trapeze; im zweiten Lösungsweg der beiden gleichschenkligen, rechtwinkligen Dreiecke) muss die Bedingung berücksichtigt werden, dass 1/4 von der äußeren Kante weiß ist. Die Kognitive Komplexität der Aufgabe lässt sich demnach ebenfalls auf Stufe 1 einordnen.
Die Formalisierung von Wissen lässt sich auf Stufe 1 ansiedeln. Eine Formel zur Ermittlung des Flächeninhalts der gelben Fläche muss eigenständig aufgestellt werden. Dabei werden bereits bekannte Formeln zur Ermittlung des Flächeninhalts von Dreiecken oder Trapezen zu Hilfe genommen. Bei dieser Einordnung wird davon ausgegangen, dass die Schülerinnen und Schüler unbekannte Längen nicht mit dem Satz des Pythagoras (der erst in der siebten Jahrgangstufe thematisiert wird (vgl. LISUM 2015, S. 26)) ermitteln, sondern in der selbst erstellten Zeichnung abmessen. Anderenfalls ließe sich die Aufgabe in Anbetracht einer sechsten Klasse auf Stufe 2 einordnen.
Lösungsroutinen sind in überschaubarem Maße erforderlich, es müssen lediglich mit den entsprechenden Formeln die Flächeninhalte berechnet werden. Somit lässt sich die Problemlöseaufgabe "Fliesenmuster" bezüglich der Formelhandhabung auf Stufe 1 einordnen. Wird allerdings der Satz des Pythagoras zur Ermittlung fehlender Seitenlängen verwendet, so sind für Lernende einer sechten Klasse anspruchsvollere Termumformungen gefordert. In diesem Fall wäre die Formelhandhabung, wie auch schon die Formalisierung von Wissen, auf Stufe 2 anzusiedeln.
Die Schülerinnen und Schüler können bei der Bearbeitung an einigen Stellen Probleme haben. Im Folgenden werden zwei dieser kritischen Stellen identifiziert und es wird aufgeführt, welche Allgemein-strategischen Hilfen, welche Inhaltsorientierten strategischen Hilfen und welche Inhaltlichen Hilfen den Lernenden in entsprechenden Situationen gegeben werden können.
Es kann für Schülerinnen und Schüler problematisch sein, auf die Idee zu kommen, zunächst die Fläche der gesamten Fliese zu berechnen und dann die Flächen der beiden weißen Dreiecke davon zu subtrahieren. In diesem Fall können folgende Hilfestellungen gegeben werden.
| Allgemein-strategische Hilfen | Inhaltsorientierte strategische Hilfen | Inhaltliche Hilfen |
| Was ist gegeben? | Welche Figuren kannst du auf der Fliese erkennen? | Wie lässt sich der Flächeninhalt von Quadraten berechnen? |
| Hast du schon einmal eine ähnliche Aufgabe gelöst? | Welche Flächen der Fliese kannst du bereits berechnen? | Wie lässt sich der Flächeninhalt von Dreiecken ermitteln? |
| Kannst du das Gesuchte direkt ermitteln? | Kannst du bekannte Flächeninhaltsformeln anwenden? | Kannst du die Länge der Katheten der weißen Dreiecke berechnen? |
Außerdem könnten die Lernenden nicht erkennen, dass die beiden weißen Dreiecke gleich groß sind. Tritt dieses Problem auf, so kann auf folgende Weise darauf eingegangen werden.
| Allgemein-strategische Hilfen | Inhaltsorientierte strategische Hilfen | Inhaltliche Hilfen |
| Was ist aus der Aufgabenstellung bekannt? | Wie lässt sich überprüfen, ob Dreiecke eine gleich große Fläche haben/deckungsgleich sind? | Wann sind Dreiecke kongruent? |
| Erinnerst du dich daran, wie man überprüfen kann, ob Dreiecke kongruent sind? | Was weißt du über die Seitenlängen und Winkel der weißen Dreiecke? | Haben die beiden weißen Dreiecke übereinstimmende Seiten und/oder Winkelgrößen? |
| Überprüfe, ob die Dreiecke wirklich den gleichen Flächeninhalt haben! | Hilft dir das Verältnis zwischen Fliesenlänge und Dreieckskathete weiter? | Denke an die Kongruenzsätze! |
- Einzelarbeit
- Partnerarbeit (eignet sich besonders für den Vergleich der Lösungswege untereinander)
Leistungsschwächeren Schülerinnen und Schülern können zusätzliche Handreichungen gegeben werden. Je nachdem wie schnell sie arbeiten, sollen sie zusätzlich zu dem folgenden Arbeitsblatt nach ihrer Rechnung auch noch eine eigene Skizze im Heft anfertigen.

Den leistungsstärkeren Schülerinnen und Schülern, die zügig mit der Aufgabe fertig sind, kann ein weiterer Arbeitsauftrag ebenfalls in Form eines Arbeitsblattes gegeben werden:

Da die Aufgabe relativ viele Teilschritte beinhaltet (Aufgabenstellung lesen und verstehen; Skizze abzeichnen; zum besseren Verständnis Figuren einzeichnen; Seitenlängen messen bzw. ausrechnen; Flächeninhalte berechnen; Flächeninhalte subtrahieren, um auf die markierte Fläche zu kommen; Lösungssatz aufschreiben; ...) ist sie auf jeden Fall für einen längeren Arbeitsaufwand einzuplanen. Durch die offen gehaltene Aufgabenstellung können die Kinder außerdem auch über mehrere Lösungswege nachdenken, mit ihren Partnern vergleichen, ihren eigenen Lösungsweg überprüfen, etc. . Plant die Lehrkraft die Aufgabe in einer interaktiven Sozialform, so kann eine ausgedehnte Übungsphase entstehen. Da geometrische Aspekte (Formen, Längen, Figuren, Flächeninhalt) sowie Themengebiete, in denen die Schülerinnen und Schüler rechnen müssen (Verhältnisse zueinander ausrechnen, um auf die Seitenlängen der Dreiecke zu gelangen), eingebettet sind, lässt sich die Aufgabe als produktive Übung einsetzen.
Bearbeitet von: Franziska Führ, Sonja Zielke (ergänzt von Marisa Pfläging)
Feedback
Wir freuen uns auf Ihre Anregungen und konstruktive Rückmeldung zum Material.
Copyright © 2014-2017 - Ana Kuzle
