Schachbrett
| Klasse | Schulstufe | Thema | Themengebiet | Schwierigkeit |
|---|---|---|---|---|
| 3/ 4 | Primarstufe | Quadrate | Größen und Messen, Raum und Form, Zahlen und Operationen | ** |
| Heuristsche Hilfsmittel | Heuristische Prinzipien | Heuristische Strategien |
|---|---|---|
| Informative Figur, Gleichungen | Zerlegungs- und Ergänzungsprinzip | Vorwärtsarbeiten, Systematisches Probieren, Analogieschlüsse |
Aufgabenstellung
Wie viele Quadrate hat ein Schachbrett?

Quellenangabe:
- Lösung
- Themengebiet
- Geförderte Kompetenzen
- Heurismen
- Schwierigkeitsgrad
- Umsetzung im Mathematikunterricht
- Einsatzmöglichkeiten
Lösungsweg 1
|
Jedes einzelne Feld des Schachbretts stellt ein 1x1-Quadrat dar:
Da in jeder Reihe und jeder Spalte jeweils acht solcher 1x1-Quadrate vorhanden sind, ergeben sich insgesamt \(8\cdot 8=64\) 1x1-Quadrate. |
|||||||||||
|
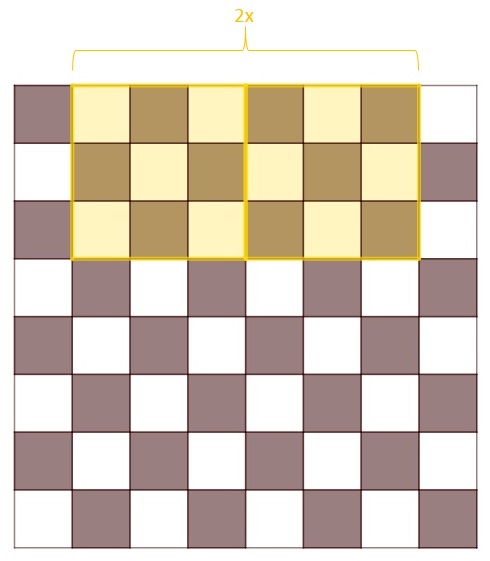
Vier Felder bilden zusammen ein 2x2-Quadrat.
Da sich längs der Seiten des Schachbretts jeweils sieben solcher Quadrate bilden lassen, existieren auf dem Schachbrett insgesamt \(7\cdot 7=49\) 2x2-Quadrate. |
|||||||||||
|
Neun Felder bilden ein 3x3-Quadrat.
Da sich in jeder Reihe und in jeder Spalte jeweils sechs 3x3-Quadrate bilden lassen, gibt es auf dem Schachbrett insgesamt \(6\cdot 6=36\) 3x3-Quadrate. |
|||||||||||
|
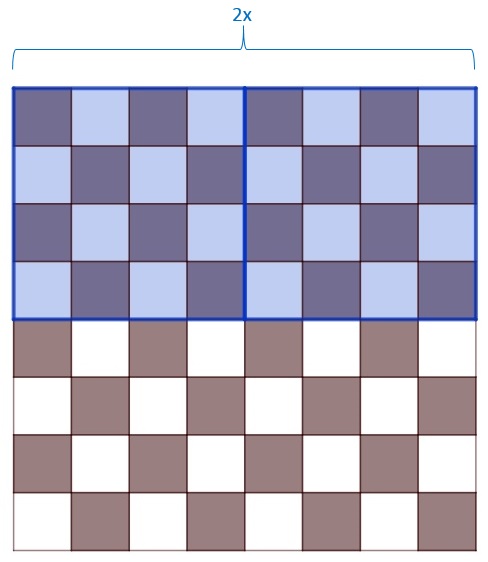
16 Felder bilden ein 4x4-Quadrat.
Da sich längs der beiden Seiten des Schachbretts jeweils fünf 4x4-Quadrate befinden, existieren auf dem Schachbrett insgesamt \(5\cdot 5=25\) 4x4-Quadrate. |
|||||||||||
|
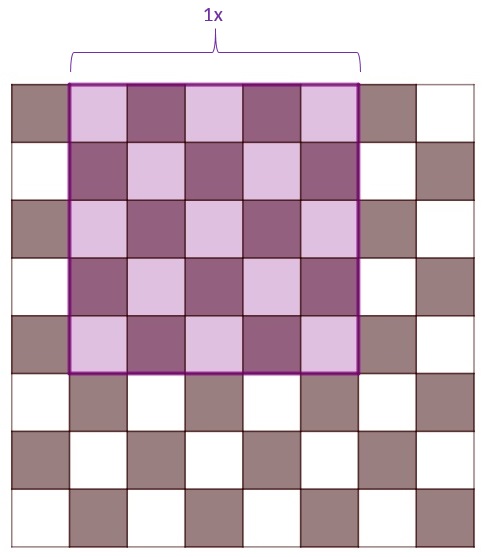
25 Schachbrettfelder bilden zusammen ein 5x5-Quadrat.
Da sich in jeder Reihe und in jeder Spalte jeweils vier 5x5-Quadrate befinden, gibt es auf dem Schachbrett insgesamt \(4\cdot 4=16\) 5x5-Quadrate. |
|||||||||||
|
36 Felder bilden zusammen ein 6x6-Quadrat.
Da sich in jeder Reihe und in jeder Spalte jeweils drei 6x6-Quadrate befnden, gibt es auf dem Schachbrett insgesamt \(3\cdot 3=9\) 6x6 Quadrate. |
|||||||||||
|
49 Felder bilden zusammen ein 7x7-Quadrat.
Da sich in jeder Reihe und in jeder Spalte jeweils zwei 7x7-Quadrate befinden, existieren insgesamt \(2\cdot 2=4\) 7x7-Quadrate auf dem Schachbrett. |
|||||||||||
|
Das gesamte Schachbrett bildet ein 8x8-Quadrat.
Da sich in jeder Reihe und jeder Spalte des Schachbretts acht Felder befinden, bildet das gesamte Schachbrett \(1\cdot 1=1\) 8x8-Quadrat. |
|||||||||||
Die Gesamtzahl N der Quadrate ergibt sich nun durch Addition der verschiedenen dargestellten Quadrate:
| NQuadrate = 64 + 49 + 36 + 25 + 16 + 9 + 4 + 1 = 204 |
Ein Schachbrett hat somit 204 Quadrate.
Bei Betrachtung des Schachbretts wird deutlich, dass Quadrate verschiedener Größe existieren.

Bei dem Brett selbst handelt es sich (bei Vernachlässigung des Randes) um ein 8x8-Quadrat, da jede Seite eine Länge von 8 Feldern hat. Aus den verschiedenen Feldern lassen sich darüber hinaus 7x7-Quadrate, 6x6-Quadrate, 5x5-Quadrate, 4x4-Quadrate, 3x3-Quadrate und 2x2-Quadrate bilden. Ein einzelnes Feld stellt außerdem ein 1x1-Quadrat dar.

Nun stellt sich die Frage, wie oft die einzelnen Quadrate auf dem Schachbrett auftreten. Eine mögliche Vorgehensweise zur Ermittlung aller Quadrate einer Größe wäre, alle möglichen Quadrate in einer Skizze einzuzeichnen und diese abzuzählen. Dieses Vorgehen kann allerdings sehr unübersichtlich sein, da sich die verschiedenen Quadrate mehrfach überschneiden.
Um die Anzahl der Quadrate für die verschiedenen Quadratgrößen besser abzählen zu können, werden für die jeweiligen Quadrat-Größen Schablonen angefertigt, die auf das Schachbrett gelegt werden können:
| 1x1-Quadrat | 2x2-Quadrat | 3x3-Quadrat | 4x4-Quadrat |
|
|
|
|
|
| 5x5-Quadrat | 6x6-Quadrat | 7x7-Quadrat | 8x8-Quadrat |
|
|
|
|
|
Es wird nun der Reihe nach - beginnend mit der gößten Schablone hin zur kleinsten - durch schrittweises Verschieben der Schablone von links nach rechts entlang jeder Zeile des Schachbretts und zeitlich paralleles Abzählen der möglichen Abdeckungen die Anzahl der Quadrate ermittelt:
|
8x8-Quadrate: Möglichkeit 1
|
Ein Schachbrett hat ein 8x8-Quadrat. | |
|
7x7-Quadrate: Möglichkeit 1 Möglichkeit 2
Möglichkeit 3 Möglichkeit 4
|
Ein Schachbrett hat vier 7x7-Quadrate. | |
|
6x6-Quadrate: Möglichkeit 1 Möglichkeit 2
Möglichkeit 3 Möglichkeit 9
|
Ein Schachbrett hat neun 6x6-Quadrate. | |
|
5x5-Quadrate: Möglichkeit 1 Möglichkeit 2
Möglichkeit 15 Möglichkeit 16 ... |
Es lassen sich 16 5x5-Quadrate zählen. | |
|
4x4-Quadrate: Möglichkeit 1 Möglichkeit 2
Möglichkeit 24 Möglichkeit 25 ... |
Es lassen sich 25 4x4-Quadrate zählen. | |
|
3x3-Quadrate: Möglichkeit 1 Möglichkeit 2
Möglichkeit 35 Möglichkeit 36 ... |
Auf dem Schachbrett lassen sich 36 3x3-Quadrate finden. | |
|
2x2-Quadrate: Möglichkeit 1 Möglichkeit 2
Möglichkeit 48 Möglichkeit 49 ... |
Es gibt 49 2x2 Quadrate auf dem Schachbrett. | |
|
1x1-Quadrate: Möglichkeit 1 Möglichkeit 2
Möglichkeit 63 Möglichkeit 64 ... |
Es gibt 64 1x1 Quadrate auf dem Schachbrett. |
Die Anzahlen der Quadrate unterschiedlicher Größe auf dem Schachbrett können nun addiert werden:
| \(1+2+9+16+25+36+49+64=204\) |
Somit hat das Schachbrett 204 Quadrate.
Die Schachbrett-Aufgabe lässt sich in der dritten oder vierten Jahrgangsstufe bei der Thematisierung von Quadraten und deren Eigenschaften einsetzen. Der Einsatz in diesen Jahrgangsstufen stimmt auch mit den geförderten Kompetenzen auf Niveaustufe B und C überein (vgl. Geförderte Kompetenzen). Eine weitere Voraussetzung für die Lösung, insbesondere für den ersten Lösungsweg, stellt die Multiplikation im Zahlenraum von 1 bis 100 sowie die Addition im Zahlenraum >100 dar. Diese sollen laut LISUM (2015) ebenfalls auf der Niveaustufe C, sprich in der dritten und vierten Klasse gefestigt werden.
Mit der Schachbrett-Aufgabe werden insbesondere die inhaltsbezogenen Kompetenzbereiche [L3] Raum und Form und [L2] Größen und Messen sowie die prozessbezogenen Kompetenzbereiche [K2] Probleme mathematisch lösen, [K3] Mathematisch modellieren und [K1] Mathematisch argumentieren aus dem brandenburgischen Rahmenlehrplan (Teil C) Mathematik für die Jahrgangsstufen 1-10 (LISUM (2015)), der ab dem Schuljahr 2017/18 gültig ist, gefördert.
Inhaltsbezogene Kompetenzformulierungen
Raum und Form [L3]
Kompetenz 1: Die Schülerinnen und Schüler grenzen die geometrische Figur "Quadrat" mithilfe von Kenntnissen über dessen Eigenschaften von anderen geometrischen Figuren ab.
"Erkennen, Benennen und Beschreiben geometrischer Objekte (Kugel, Würfel, Quader sowie Dreieck, Viereck, Quadrat, Rechteck, Kreis) in der Umwelt und am Modell unter Nennung einzelner Merkmale" (LISUM, 2015, Geometrische Objekte und Ihre Eigenschaften beschreiben, Niveaustufe B, S.46)
Erläuterung: Die Schülerinnen und Schüler wissen, dass Quadrate vier Ecken haben und jeweils zwei zueinander parallele Seiten, wobei alle Seiten die gleiche Länge haben. Diese Kenntnisse sind notwendig um die möglichen Quadrate auf dem Schachbrett identifizieren zu können.
Kompetenz 2: Die Schülerinnen und Schüler verschieben Quadrate einer bestimmten Größe gedanklich oder enaktiv mithilfe von Schablonen auf dem Schachbrett, um die Anzahl der möglichen Quadrate dieser Größe ermitteln zu können.
"Die Schülerinnen und Schüler können Lage- und Größenveränderungen bei geometrischen Figuren ausführen" (LISUM, 2015, Geometrische Abbildungen ausführen, Niveaustufe C, S.27)
Erläuterung: Um die Anzahl aller möglichen Quadrate zu ermitteln wird in der Größe der Quadrate, die betrachtet werden, variiert und diese verschiedenen Quadrate werden dann systematisch auf dem Schachbrett verschoben bis alle Möglichkeiten gefunden sind.
Größen und Messen [L2]
Kompetenz 3: Die Schülerinnen und Schüler stellen sich durch Vergleichen des Umfangs und Flächeninhalts von möglichen Quadraten (wobei ein Schachbrettfeld als Einheitsgröße gesehen wird) mit den Feldern des Schachbretts vor, wie viele Quadrate einer bestimmten Größe auf dem Schachbrett wiederzufinden sind.
"Ermitteln des Umfangs von geradlinigen ebenen Figuren durch Auszählen von Einheitslängen", "Ermitteln des ungefähren Flächeninhalts von geradlinigen ebenen Figuren durch Auszählen von Einheitsflächen", (LISUM, 2015, Größenangaben bestimmen, Niveaustufe C, S.40)
Erläuterung: Um die Anzahl verschiedener Quadrate auf dem Schachbrett ermitteln zu können, müssen die Lernenden die Seitenlängen der jeweiligen betrachteten Quadratgröße mit den Feldern des Schachbretts abgleichen, um zu entscheiden, ob das jeweilige Quadrat noch einen Bereich vom Schachbrett abdeckt. Die Schablonen, die beim zweiten Lösungsweg angefertigt werden, erleichtern dies.
Prozessbezogene Kompetenzformulierungen
Probleme mathematisch lösen [K2]
Kompetenz 4: Die Schülerinnen und Schüler nutzen die Heuristischen Strategien des Systematischen Probierens und der Analogieschlüsse, um die Aufgabe zu lösen.
"Die Schülerinnen und Schüler können Lösungsstrategien (z.B. vom Probieren zum systematischen Probieren) entwickeln und nutzen" (LISUM, 2015, S.19)
Erläuterung: vgl. Heurismen
Mathematisch modellieren [K3]
Kompetenz 5: Die Schülerinnen und Schüler reduzieren ein reales Problem auf die wesentlichen Elemente, die für dessen Lösung von Bedeutung sind.
"Die Schülerinnen und Schüler können reale Situationen strukturieren und vereinfachen" (LISUM, 2015, S.20)
Erläuterung: Bei der Lösung der Aufgabe reduzieren die Lernenden das Schachbrett auf das Raster, welches durch die Felder gegeben ist, wobei sie die Farbe der Felder vernachlässigen.
Mathematisch argumentieren [K1]
Kompetenz 6: Die Schülerinnen und Schüler begründen ihren Lösungsweg bei der Lösungsdokumentation und -präsentation.
"Die Schülerinnen und Schüler können Begründungen [...] zunehmend selbstständig entwickeln." (LISUM, 2015, S.19)
- Beim ersten Lösungsweg werden Informative Figuren und Gleichungen zum Ermitteln der Anzahlen der Quadrate einer bestimmten Größe verwendet.
- Bei beiden Lösungswegen wird die Strategie des Systematischen Probierens angewandt, indem geforscht wird, wie oft ein Quadrat einer bestimmten Größe (beispielsweise ein 2x2-Quadrat) in jede Reihe/Spalte passt.
- Für weitere Quadratgrößen wird dann analog vorgegangen. Somit werden für das weitere Vorgehen mit anderen Quadraten Analogieschlüsse gezogen bis alle Quadratgrößen "abgearbeitet" sind.
- Bei den Lösungen wird jeweils das Gegebene (das Schachbrett, das Quadrat als geometrische Figur) betrachtet und überlegt, was über das Gegebene bekannt ist (das Schachbrett setzt sich aus 8x8 quadratischen Feldern zusammen, ein Quadrat hat zwei gleich lange Seiten) und es wird überlegt, welche Teilziele (die Anzahlen der verschiedenen Quadratgrößen) erreicht werden können, um zum Gesuchten (der Anzahl aller Quadrate auf dem Schachbrett) zu gelangen. Somit wird in den beiden Lösungswegen vorwärts gearbeitet.
- Bei der Lösung der Schachbrett-Aufgabe wird das große 8x8-Quadrat in kleinere Quadrate (1x1-, 2x2-, 3x3-, 4x4-, 5x5-, 6x6- und 7x7-Quadrate) zerlegt und zunächst die Anzahl der Quadrate dieser verschiedenen Größen ermittelt. Somit wird das Zerlegungsprinzip genutzt.
Die Schachbrett-Aufgabe hat nach Cohors-Fresenborg et al. mit insgesamt 5 erreichten Punkten bezüglich der ersten Lösungsmöglichkeit und 3 erreichten Punkten bezüglich der zweiten Lösungsmöglichkeit einen Schwierigkeitsgrad von **.
Die Sprachlogische Komplexität der Aufgabe entspricht der Stufe 1, da es sich bei der Frage in der Aufgabenstellung zwar um einen einfachen Hauptsatz handelt, dieser jedoch keine Hinweise auf die Schritte bei der mathematischen Bearbeitung gibt. Darüber hinaus sind zwar nicht im Aufgabentext an sich unrelevante Zusatzinformationen enthalten, allerding in der Abbildung des Schachbretts, auf dem verschiedenfarbige Felder vorhanden sind. Die Unterscheidung der schwarzen und weißen Felder ist jedoch für die Lösung unrelevant.
Die Schülerinnen und Schüler müssen sich vor der Lösung der Aufgabe überlegen, wie sie am Besten vorgehen. Entscheidend dafür, alle Quadrate zu finden, ist zunächst die Unterteilung in Quadrate verschiedener Größen. Es werden also verschiedene Fälle betrachtet und die Lernenden sollten sich eigenständig überlegen, wie sie am Besten vorgehen (durch Systematisches Probieren). Die Aufgabe lässt sich damit in Anbetracht des Einsatzes in einer dritten oder vierten Grundschulklasse bezüglich der Kognitiven Komplexität auf der Stufe 2 ansiedeln.
Die Formalisierung von Wissen entspricht bezüglich des ersten Lösungsweges der Stufe 1, da Formeln zur Ermittlung der Anzahlen der verschiedenen Quadratgrößen aufzustellen sind. Beim zweiten Lösungsweg wird die Anzahl der Quadrate mithilfe von Schablonen abgezählt. Lediglich zur Ermittlung der Gesamtzahl der Quadrate werden die Anzahlen der verschiedenen Quadratgrößen mithilfe einer Formel addiert. Deshalb entspricht die Formalisierung von Wissen bezüglich des zweiten Lösungsweges eher der Stufe 0.
Auch die Formelhandhabung lässt sich bezüglich des ersten Lösungsweges auf Stufe 1 einordnen und bezüglich des zweiten Lösungsweges auf Stufe 0, da beim ersten Lösungsweg jeweils die Anzahl der Quadrate entlang einer Seite des Schachbretts mit der Anzahl der Quarate entlang der anderen Seite des Schachbretts multipliziert wird, um die Gesamtzahl der Quadrate einer bestimmten Größe zu ermitteln. Beim zweiten Lösungsweg werden die Quadrate hingegen lediglich abgezählt. Lösungsroutinen werden damit beim ersten Lösungsweg in überschaubarem Maße erfordert und beim zweiten Lösungsweg lediglich bei der Ermittlung der Gesamtzahl der Quadrate.
Bei der Lösung der Schachbrett-Aufgabe können die Schülerinnen und Schüler einer dritten oder vierten Grundschulklasse an verschiedenen Stellen Schwierigkeiten haben. Im Folgenden sind zwei solcher kritischen Stellen dargestellt und es werden jeweils Vorschläge gemacht, welche Hilfen den Lernenden in solchen Fällen bezüglich des Lösungsprozesses an sich, bezüglich fachbezogener Lösungsstrategien oder bezüglich des Inhalts gegeben werden können.
Es könnte für die Schülerinnen und Schüler schwierig sein, zu erkennen, dass nicht nur das Schachbrett an sich und die einzelnen Schachbrettfelder jeweils ein Quadrat bilden sondern dass auch verschiedene Schachbrettfelder zusammen weitere Quadrate bilden. In diesem Fall können den Lernenden die folgenden in der Tabelle aufgeführten Allgemein-strategischen, inhaltsorientierten strategischen oder inhaltlichen Hilfen gegeben werden.
| Allgemeine strategische Hilfen | Inhaltsorientierte strategische Hilfen | Inhaltliche Hilfen |
| Was ist gegeben? | Gibt es bestimmte Linien auf dem Schachbrett, die dir weiterhelfen könnten? | Wie groß ist der Flächeninhalt des Schachbretts? |
| Untersuche das Gegebene! | Kannst du das Schachbrett in Teilfiguren zerlegen? | Mit welchen Längeneinheiten lassen sich die Seiten des Schachbretts beschreiben? |
| Fertige doch weitere Skizzen an! | Kannst du das Schachbrett in weitere Quadrate zerlegen? | Es gibt noch mehr Quadrate auf dem Schachbrett! |
Außerdem könnten die Schülerinnen und Schüler nicht auf die Idee kommen, systematisch die einzelnen Zeilen und Spalten des Schachbretts zu betrachten und so die Anzahlen der verschiedenen Quadrate zu ermitteln. Tritt dieses Problem auf, können den Lernenden die folgenden Hilfestellungen gegeben werden.
| Allgemeine strategische Hilfen | Inhaltsorientierte strategische Hilfen | Inhaltliche Hilfen |
| Wie kannst du deine Lösung überprüfen? | Kannst du rechnerisch vorgehen? | Wie viele Möglichkeiten gibt es für ein Quadrat einer bestimmten Größe? |
| Gehe systematisch vor! | Berücksichtige die Zeilen und Spalten auf dem Schachbrett! | Lassen sich die Quadrate verschiedener Größen systematisch verschieben? |
| Kannst du die Anzahlen der verschiedenen Quadrate überprüfen? | - | - |
- Einzelarbeit
- Partnerarbeit
- Gruppenarbeit
Die Schachbrettaufgabe kann sowohl für leistungsschwächere als auch für leistungsstärkere Schülerinnen und Schüler so abgewandelt werden, dass sie eine angemessene Herausforderung darstellt.
Für leistungsschwächere Schülerinnen und Schüler können folgende Änderungen an der Aufgabe vorgenommen werden:
- Die Quadrate, die gefunden werden sollen können auf bestimmte Quadrate, beispielsweise die 1x1-Quadrate und die 8x8-Quadrate, reduziert werden, sodass die Lernenden nur die Strategie des einfachen Abzählens der Kästchen anwenden müssen. Zusätzlich bei dieser Einschränkung der Aufgabe kann dann noch nach der Anzahl der weißen und schwarzen Quadrate gefragt werden.
- Bei Betrachtung der beiden Lösungswege ist auffällig, dass die Aufgabe an sich durch die Lösungen verschiedener Schwierigkeit bereits differenziert. So wird beim ersten Lösungsweg mit Skizzen gearbeitet und es werden jeweils die Anzahlen der Quadrate einer bestimmten Größe berechnet, wohingegen beim zweiten Lösungsweg auf enaktiver Ebene gearbeitet wird und die Schülerinnen und Schüler die einzelnen Quadrate mithilfe der Schablonen besser erkennen können und diese einfacher abzählen können. Leistungsschwächeren Schülerinnen und Schülern könnte daher von vornherein der Hinweis gegeben werden, sich Schablonen der verschiedenen Quadrate, die auf dem Schachbrett auftreten, zu basteln und diese auf dem Schachbrett hin- und herzuschieben, um alle Quadrate zu finden.
Auch für leistungsstärkere Schülerinnen und Schüler gibt es Möglichkeiten die Aufgabe schwieriger zu gestalten:
- Die Aufgabe könnte erweitert werden, indem zusätzlich nach der Anzahl der Rechtecke auf dem Schachbrett gefragt wird.
- Anstelle nach der Anzahl der Quadrate könnte nach der Anzahl der Vierecke auf dem Schachbrett gefragt werden, sodass sowohl die Anzahl aller Quadrate als auch die Anzahl aller weiteren Rechtecke ermittelt werden soll.
Die Schachbrettaufgabe eignet sich zum Forschen, da das Schachfeld Raum für Entdeckungen lässt. So können verschieden große Quadrate entdeckt werden. Außerdem kann die Aufgabe als langfristige Hausaufgabe aufgegeben werden, denn auch manch ein Erwachsener wird der Lösung nicht sofort auf den Grund gehen können, sodass die Kinder eventuell beispielsweise mit ihren Eltern darüber sprechen und rätseln können. Sollten einzelne Kinder ausschließlich die Zählstrategie verwenden (beispielsweise wie in Lösungsweg 2), so haben sie im Rahmen einer Hausaufgabe ausreichend Zeit für die Lösung. Die Aufgabe kann darüber hinaus aber auch zum produktiven Üben eingesetzt werden, da die Schülerinnen und Schüler durch die Lösung den Umgang mit Quadraten und das Erkennen von Quadraten festigen und diese geometrischen Figuren von anderen Figuren abgrenzen können. So ist beispielsweise ein 2x1-Feld kein Quadrat, sondern ein Rechteck und dieses wird daher nicht mitgezählt. Das Rechnen im Zahlenraum von 1 bis 100 und darüber hinaus wird wiederholt und angewendet. Außerdem werden Lösungsstrategien angewandt und somit gefestigt.
Bearbeitet von: Nina Kühne, Dora Malleike, Katja Pusch, Patricia Schütze (ergänzt von Marisa Pfläging)
Feedback
Wir freuen uns auf Ihre Anregungen und konstruktive Rückmeldung zum Material.
Copyright © 2014-2017 - Ana Kuzle