Winkelberechnung am Dreieck
| Klasse | Schulstufe | Thema | Themengebiet | Schwierigkeit |
|---|---|---|---|---|
| 7 | Sekundarstufe I | Größen und Messen, Raum und Form | *, ** |
| Heuristsche Hilfsmittel | Heuristische Prinzipien | Heuristische Strategien |
|---|---|---|
| Informative Figur, Lösungsgraphen, Gleichungen | Zerlegungs- und Ergänzungsprinzip, Symmetrieprinzip | Vorwärtsarbeiten, Systematisches Probieren, Analogieschlüsse |
Aufgabenstellung

Quellenangabe:
- Lösung
- Themengebiet
- Geförderte Kompetenzen
- Heurismen
- Schwierigkeitsgrad
- Umsetzung im Mathematikunterricht
- Einsatzmöglichkeiten

Zunächst kann man den Winkel α an A mithilfe des gestreckten Winkels bestimmen. Nach dem Nebenwinkelsatz beträgt dieser 180°-141° = 39° = α. Nun kann man das Dreieck \(\triangle ABC\) in zwei Innendreiecke \(\triangle ADC\) und \(\triangle BCD\) unterteilen. Aufgrund des Kreisbogens um D, auf dem die Punkte A und C liegen, erkennt man, dass das Dreieck \(\triangle ADC\) gleichschenklig sein muss und somit die Strecken \(\overline { AD } \) und \(\overline { DC } \) gleich lang sein müssen. Aufgrund der Eigenschaften eines gleichschenkligen Dreiecks müssen dementsprechend auch die Winkel \(\measuredangle DAC\) und \(\measuredangle ACD\) gleich groß sein. Dementsprechend setzt sich die Winkelsumme im Dreieck \(\triangle ADC\) so zusammen: α + α + β = 180°(Winkelsummensatz im Dreieck). Also muss β = 180° – α – α = 180° - 39° - 39° = 102° sein. Nun kann man δ bestimmen, indem man den gestreckten Winkel an D nutzt. Da nach dem Nebenwinkelsatz β + δ = 180° gilt, muss δ = 180° - β = 180° - 102° = 78° sein. Nun betrachten wir das Dreieck \(\triangle BCD\). Hier erkennen wir, dass die Punkte B und D auf dem Kreisbogen um C liegen, also die Strecken \(\overline {CB}\) und \(\overline {CD}\) gleich lang sind. Das Dreieck \(\triangle BCD\) ist also ein gleichschenkliges Dreieck und dementsprechend müssen die Winkel \(\measuredangle BDC\) und \(\measuredangle CBD\) gleich groß sein. Der Winkel an B ist also genauso groß wie δ und damit 78° groß. Nun können wir wieder das Dreieck \(\triangle ABC\) betrachten. Nach dem Innenwinkelsummensatz eines Dreiecks gilt α + γ + δ = 180°. α und δ kennen wir, also ist γ = 180° - α – δ = 180° - 39° - 78 ° = 63°. Somit ist die Aufgabe gelöst.

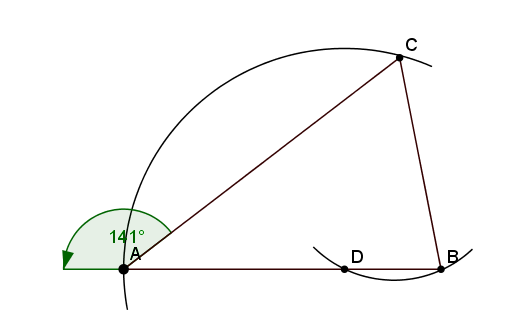

Den Winkel \(\measuredangle DAC\) misst man nun mithilfe des Geodreiecks und erhält den Wert 39°. Nun sucht man sich einen beliebigen Punkt D auf der Geraden g und zeichnet mithilfe eines Zirkels einen Kreis mit dem Radius der Strecke \(\overline {DA}\) um D. Dieser schneidet h in einem Punkt C, weil D laut Skizze der Mittelpunkt eines Kreises ist, auf dem A und C liegen. Weil wir zwei Winkel des Dreiecks \(\triangle {ADC}\), welches wir konstruieren möchten, kennen, ist der dritte festgelegt. Da die Winkel festgelegt sind, ist das Dreieck eindeutig und die Seitenlängen stehen immer im gleichen Verhältnis zueinander – egal ob es gestreckt oder gestaucht wird. Und weil wir keine Seitenlängen berechnen wollen, sondern nur Winkel, darf D beliebig auf g liegen, solange D rechts von A liegt. Nun zeichnen wir mit dem Geodreieck die Strecke \(\overline {DC}\) ein, können mit dem Geodreieck den Winkel \(\measuredangle CDA\) messen und erhalten den Wert 101°.


Laut dem Kerncurriculum Niedersachsen für Realschulen 2014 (KC) ist dieses Thema in allen Jahrgangsstufen ein wichtiger inhaltlicher Aspekt, der in den inhaltsbezogenen Kompetenzen "Größen und Messen" sowie "Raum und Form" gefördert wird.
"Die Schülerinnen und Schüler unterscheiden Dreiecksformen." (KC, Ende zusätzlich Schuljahrgang 8, S.28)
Ein gleichschenkliges Dreieck besitzt zwei gleich große Winkel, die an der Grundseite anliegen. Durch diese entstehen auch zwei gleichlange Schenkellängen. Die Schenkel schließen dabei den drittel Winkel ein. In der Aufgabenbearbeitung wird mit zwei gleichschenkligen Dreiecken gearbeitet, die durch die Kreisbögen und eine Verbindung der Kreisbogenmittelpunkte entstehen. Sie ergeben sich aus dem bei einem Kreis immer gleich großen Radius. Dadurch, dass immer zwei Winkel gleichgroß sind, hat man direkt Informationen über mehrere Winkel und kann dann leichter die restlichen erarbeiten.
"Die Schülerinnen und Schüler konstruieren geometrische Figuren mit Zirkel und Geodreieck [...]." (KC, Ende zusätzlich Schuljahrgang 8, S.28)
"Die Schülerinnen und Schüler wenden den Winkelsummensatz für Drei- [...]ecke an." (KC, Ende zusätzlich Schuljahrgang 8, S.28)
Dies geschieht sowohl mehrfach bei der Errechnung des dritten Winkelmaßes in einem gleichschenkligen Dreieck und bei der Errechnung des gesuchten Winkels am Ende des Lösungsweges (180° - α – δ = γ).
"Die Schülerinnen und Schüler gliedern das Problem in Teilprobleme." (KC, Ende zusätzlich Schuljahrgang 8, S.19)
"Die Schülerinnen und Schüler entnehmen Informationen aus komplexen Grafiken und Diagrammen und interpretieren diese." (KC, Ende zusätzlich Schuljahrgang 8, S.21)
"Die Schülerinnen und Schüler erläutern Mitschülerinnen und Mitschülern ihre Überlegungen, die zur Lösung geführt haben." (KC, Ende zusätzlich Schuljahrgang 8, S.23)
- Als heuristische Hilfsmittel wird sich einer informativen Figur bedient, die die Skizze bereits vorgeliefert hatte und von den Schülerinnen und Schülern durch zusätzliche Ideen für den Lösungsweg erweitert wurde. Ein Lösungsgraph wurde sozusagen im Kopf erstellt. Die unterschiedlichen Ideen und Lösungsschritte werden durchgegangen, es werden sich mögliche Zwischenergebnisse gemerkt und so wird über eine geplante Vorgehensweise mit fester Reihenfolge zum Ziel gelangt.
- Desweiteren werden Gleichungen als heuristisches Hilfsmittel verwendet: Beziehungen in einem Dreieck und einem Kreis wie beispielsweise Winkelmaßgrößen, Längenverhältnisse und Radius müssen bedacht werden. Außerdem wird der Innenwinkelsatz angewendet.
- Als heuristische Strategie wird das Vorwärtsarbeiten verwendet. Durch eine Angabe erhalten die Schülerinnen und Schüler weitere Information, die wiederum zu einer weiteren verhilft. Es werden also schrittweise Erkenntnisse gesammelt, die dann zum gesuchten Ziel führen.
- Beim systematischen Probieren geht es um die Suche nach Zusammenhängen. Auch in der Skizze müssen zunächst Zusammenhänge betrachtet und gefunden werden, sodass das Problem und die Lösungsansätze besser verstanden werden.
- Außerdem können Analogieschlüsse aus alten Übungsaufgaben zum Beispiel zum Thema Innenwinkelsummensatz gezogen werden.
-
Es werden die heuristischen Prinzipien Zerlegen und Ergänzen sowie das Symmetrieprinzip angesprochen. Das erste Prinzip findet man beim Ergänzen von Winkeln und Strecken, wenn die Kreismittelpunkte verbunden werden. Durch diese Ergänzung wird gleichzeitig das gegebene Dreieck in zwei gleichschenklige Dreiecke zerlegt, wodurch man wiederum neue Winkel ergänzen kann. Das Symmetrieprinzip wird durch die gleichschenkligen Dreiecke angesprochen, deren eine Winkelhalbierende immer auch eine Symmetrieachse ist, woraus gewisse Winkelbeziehungen entstehen.
| Allgemein-strategische Hilfen | Inhaltsorientierte strategische Hilfen | Inhaltliche Hilfen |
|
Hast du eine ähnliche Aufgabe schon einmal gelöst?
|
Kannst du das Dreieck einteilen? |
Verbinde die Kreismittelpunkte - welche Dreiecke erhältst du? |
|
Was siehst du an der Skizze?
|
Siehst du besondere Dreiecke? |
Kannst du das Dreieck so unterteilen, dass du gleichschenklige Dreiecke erhältst? |
| Was ist gegeben? | Was sagen dir die Kreisbögen? | Rechtwinklige Dreiecke helfen dir nicht weiter. |
| Allgemein-strategische Hilfen | Inhaltsorientierte strategische Hilfen | Inhaltliche Hilfen |
|
Was hast du gegeben? |
Gibt es gleiche Winkel in diesem Dreieck? |
Welche Winkel sind beim gleichschenkligen Dreieck gleich? |
|
Schau dir an, welche Schritte du zuerst machen musst; womit musst du anfangen? |
Kannst du bekannte Sätze anwenden? |
Was sagt der Nebenwinkelsatz aus? |
| Was bringt dir die Unterteilung? |
Was weißt du über Winkel in Dreiecken? |
Was sagt der Innenwinkelsummensatz aus? |
- Partnerarbeit
Für leistungsstärkere Schülerinnen und Schüler kann beispielsweise die Berechnung mehrerer Winkel verlangt werden, wie zum Beispiel die des Winkels ε im rechnerischen Teil der Aufgabe. Außerdem könnte zum Beispiel eine weitere Variante der Aufgabe gestellt werden, indem zum Beispiel der Anfangswinkel verändert wird, oder indem eine Bedingung geändert wird, zum Beispiel, dass anstatt der Thematik von gleichschenkligen Dreiecken rechtwinklige Dreiecke herangezogen werden.
Außerdem spielt der Kreis und seine Eigenschaften eine wichtige Rolle in dieser Aufgabe. Da der Kreis bis zur sechsten Klasse thematisiert worden sein soll, ist diese Aufgabe zur Auffrischung des Wissens, welches aus vorherigen Schuljahren bereits vorhanden sein sollte, geeignet und daher recht vielfältig.
Bearbeitet von: Matthias Schmidt, Esther Schnepel (hochgeladen von Marisa Pfläging)
Feedback
Wir freuen uns auf Ihre Anregungen und konstruktive Rückmeldung zum Material.
Copyright © 2014-2017 - Ana Kuzle
